Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 2.3 - Ex. 21
Três fábricas fornecem equipamentos de precisão para o laboratório de química de uma universidade. Apesar de serem aparelhos de precisão, existem uma pequena chance de subestimação ou superestimação das medidas efetuadas. A tabela a seguir apresenta o comportamento do equipamento produzido em cada fábrica:
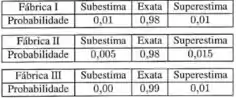
As fábricas I, II e III fornecem, respectivamente, 20%, 30% e 50% dos aparelhos utilizados. Escolhemos, ao acaso, um desses aparelhos e perguntamos a probabilidade de:
- Haver superestimação de medidas?
- Não haver subestimação das medidas efetuadas?
- Dando medidas exatas, ter disso fabricado em III?
- Ter sido produzido por I, dado que não subestima as medidas?
Passo 1
Em (a) temos de encontrar a probabilidade de haver a superestimação de medidas ao pegar um aparelho produzido por uma das 3 fábricas, daí, teremos:
Passo 2
Em (b) queremos encontrar a probabilidade de não haver subestimação das medidas efetuadas, ou seja, podemos ter medidas superestimadas e medidas exatas, assim:
Passo 3
Em (c), dando medidas exatas, querendo encontrar a probabilidade de termos aparelhos fabricados pela fábrica III. Para isso, vamos encontrar inicialmente a probabilidade de dar medidas exatas, assim:
Agora, vamos calcular a probabilidade condicional, sabendo a probabilidade das medidas serem exatas, vamos encontrar a probabilidade do aparelho ser da fábrica III, assim:
Passo 4
Em (d) sabemos que os aparelhos tem medidas não subestimadas, então, queremos saber a probabilidade de terem sido feitos pela fábrica I. Já calculamos a probabilidade das medidas não serem subestimadas, assim:
Resposta
Logo,
- 0,0115;
- 0,9965;
- 0,5025;
- 0,1987.