Enunciado
Probabilidade e Estatística - Probabilidade, um curso moderno com aplicações, de Sheldon Ross- Ed: 8º - Capítulo 1.Problemas - Ex. 15
Uma turma de dança é formada por 22 estudantes, dos quais 10 são mulheres e 12 são homens. Se 5 homens e 5 mulheres forem escolhidos para formar pares, quantas combinações diferentes serão possíveis?
Passo 1
Opa galeeeeera! Hoje vamos rever o princípio fundamental da contagem (PFC).
Vamos pensar que cada casal é como se fosse um lugar separada em uma fila:
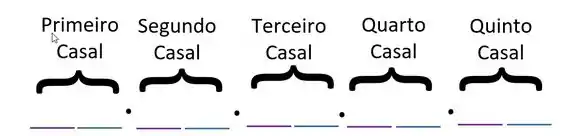
A nossa estratégia será ver quantas opções temos para cada casal, e depois utilizar o PFC para encontrar as combinações possíveis.
Passo 2
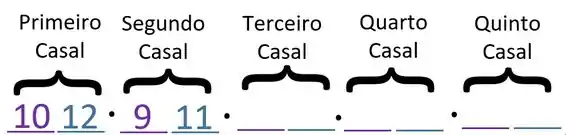
Vamos começar pelo primeiro casal, existem 10 mulheres que podem ser a mulher do primeiro casal, e 12 homens que podem ser o homem do primeiro casal. Então vamos anotar isto.
Já escolhemos um homem e uma mulher, sobraram 9 mulheres e 11 homens, e agora teremos 9 opções de mulheres e 11 de homens para o segundo casal, anotando:
Passo 3
Podemos notar que a cada casal que escolhemos é removido um homem e uma mulher da lista de opções para o próximo casal, então podemos subtrair uma unidade a cada casal. Assim a nossa anotação se torna:
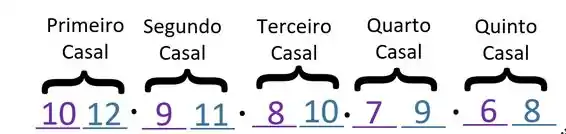
Segundo o PFC a cada vez que aparece um “e” no nosso argumento teremos que multiplicar as possibilidades de cada caso, como vimos a cima entre cada casal e entre os homens e mulheres aparecia um “e” no argumento.
Então multiplicando tudo:
Passo 4
Mas aqui tem um porem, neste caso nós definimos a ordem dos casais, o que não faz sentido, pois, se fossem o casal Beatriz e João e depois o casal Maria e Lucas ou o contrario seria a mesma coisa.
Então estamos contando as permutações dos casais também, e isso não é necessário. Para eliminarmos estas repetições basta dividirmos pela permutação do numero de casais. Como temos 5 casais:
Então há 23950080 possibilidades de se formar estes 5 casais.