Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 8.Problemas - Ex. 37a

Uma urna contém três bolas numeradas 0, 1, 2. Duas bolas são retiradas ao acaso e sucessivamente. Sejam as v.a. X = número da primeira bola retirada e Y = número da segunda bola retirada. Calcule E(XY) para quando a bola é retirada com reposição e sem reposição.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para pegar o que aconteceu lá na combinação das variáveis e encontrar a esperança mútua dos dois eventos. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser montar uma tabela com todos os dados que ele nos deu no enunciado.

No caso da reposição, temos:

Para sem reposição, nossa tabela fica:

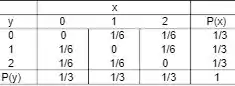
Passo 3

Pronto!! Agora é só fazer os cálculos das esperanças!!

E r   X Y = 1 9 { 0 + 0 + 0 + 0 + 1 + 2 + 0 + 2 + 4 }

E r   X Y = 1

E s   X Y = 1 6 { 0 + 0 + 0 + 0 + 2 + 0 + 2 }

E s   X Y = 2 3

Resposta

E r   X Y = 1

E s   X Y = 2 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O exemplo a seguir ilustra que ρ = 0 não implica independência. Suponha que (X, Y)tenha distribuição conjunta dada pela tabela abaixo. Justifique por que X e Y não são independentes.
O exemplo a seguir ilustra que ρ = 0 não implica independência. Suponha que (X, Y)tenha distribuição conjunta dada pela tabela abaixo. Mostre que E(XY) = E(X) E(Y), donde ρ = 0.
Se E(X) = μ e Var(X) = σ², escreva em função de μ e σ² as seguintes expressões:E(X²)
Suponha que realizemos um experimento e os resultados possíveis sejam w1, w2, w3, w4, w5.Definamos as v.a. X e Y cujos valores em cada ponto são dados na tabela a seguir.Obtenha as distribuições de pr
Numa sala estão cinco crianças cujas idades são (em anos): 3, 3, 4, 5, 5. Escolhem-se três crianças ao acaso para formar uma trinca. X indica a idade da mais nova da turma, e Y à da mais velha. Calcul