Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 2.Problemas - Ex. 2
Usando os dados da Tabela , construa a distribuição de frequências das variáveis:
Estado civil.
Região de procedência.
Número de filhos dos empregados casados.
Idade.
Passo 1
Bom galera, vamos começar construindo a tabela de estado civil, se a gente contar a gente encontra casados e solteiros, assim, a proporção de casados é:
E de solteiros:
Assim a tabela fica:
Passo 2
Belezinha, a gente faz o mesmo para a região de procedência:
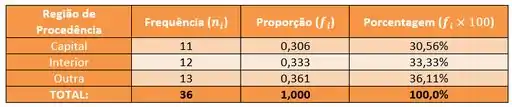
E com o número de filhos dos empregados casados, a gente tem que separar um grupo pegando apenas os empregados casados da amostra e na tabela fica:
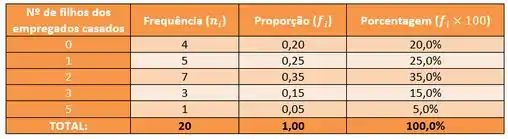
Passo 3
Show de bola, nesse último a gente vai dividir a idade em intervalos de em anos, logo iremos ter:
E fazendo a tabela ficamos com:
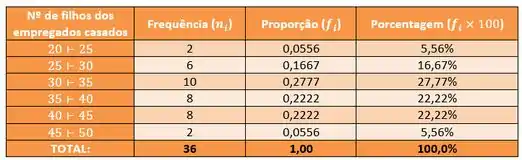
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Prove (8.9) para v.a. X e Y contínuas.
Suponha que X e Y sejam v.a. com Var(X) = 1, Var(Y) = 2 e ρ(X, Y) = 1/2. Determine Var(X – 2Y).
Uma urna contém n bolas numeradas de 1 até n. Duas bolas são retiradas sucessivamente, sem reposição. Determine a distribuição do módulo da diferença entre os dois números observados.
Se ρ(X, Y) for o coeficiente de correlação entre X e Y, e se tivermos que Z = AX + B, W = CY + D, com A0, C0, prove que ρ(X, Y) = ρ(Z, W).
Se X~N(μ1, σ1²) e Y~N(μ2, σ2²), e se X e Y são independentes, encontre a distribuição, a média e a variância da v.a. aX + bY, a e b constantes..