Usando um gráfico de barras para encontrar probabilidades - Nos exercícios 63 a 66, use o gráfico de barras a seguir, que mostra o maior nível educacional atingido pelos funcionários de uma empresa. Ache a probabilidade de que o maior nível educacional de um

funcionário escolhido aleatoriamente seja:

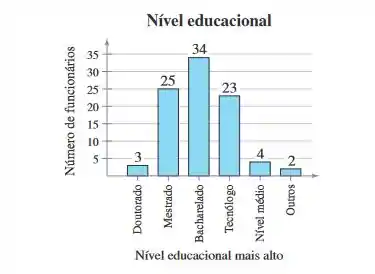
66. Ensino médio.

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Primeiro, vamos determinar o evento, que é o nível mais alto de educação do funcionário é um diploma de ensino médio, vamos denominar por , ok, o número de resultados possíveis é o número de funcionários (no total) e o número de funcionários para cada tipo de grau é dado acima de cada barra na barra gráfico e, portanto, o número de resultados possíveis é, portanto, a soma de todos esses valores. Logo,

Observamos então que a frequência do diploma do ensino médio é 4 (dado acima da barra do diploma do ensino médio) no gráfico de barras fornecido e, portanto, existem 4 resultados favoráveis.