Usando-se o histograma, podemos derivar um procedimento alternativo para encontrar a mediana de uma variável. Pela sua definição vemos que ela deve corresponder ao valor da abscissa que divide a área do histograma em duas partes iguais (50% para cada lado). Então, usando argumentos geométricos, podemos encontrar um ponto, satisfazendo essa propriedade. Vejamos como proceder através de um exemplo.

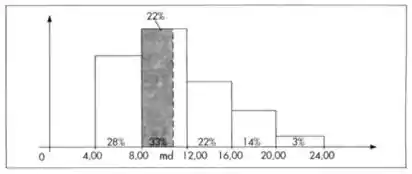
Devemos localizar o ponto das abscissas que divide o histograma ao meio. A área do primeiro retângulo corresponde a do total, os dois primeiros a ; portanto, a mediana é algum número situado entre . Ou melhor, a mediana irá corresponderão valor no segundo retângulo, cuja área do retângulo de base é a mesma altura que o retângulo de base seja ( do primeiro retângulo mais do segundo, perfazendo os ). Consulte a figura para melhor compreensão. Pela proporcionalidade entre a área e a base do retângulo, temos:

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de estática básica do morettin usando histograma, podemos derivar um procedimento alternativo para encontrar a mediana de uma variável. Pela sua definição vemos que ela deve corresponder ao valor da abscissa que divide a área do histograma em duas partes iguais (50% para cada lado). Então, usando argumentos geométricos, podemos encontrar um ponto, satisfazendo essa propriedade. Vejamos como proceder através de um exemplo.

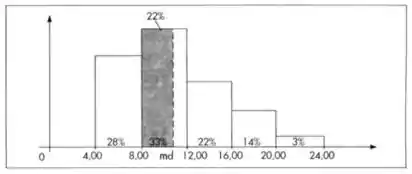
Devemos localizar o ponto das abscissas que divide o histograma ao meio. A área do primeiro retângulo corresponde a do total, os dois primeiros a ; portanto, a mediana é algum número situado entre . Ou melhor, a mediana irá corresponderão valor no segundo retângulo, cuja área do retângulo de base é a mesma altura que o retângulo de base seja ( do primeiro retângulo mais do segundo, perfazendo os ). Consulte a figura para melhor compreensão. Pela proporcionalidade entre a área e a base do retângulo, temos:

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.