Você já imaginou se os jogadores de futebol sofressem efeitos adversos ao cabecear a bola? Os autores do artigo "No Evidence of Impaired Neurocognitive Performance in Collegiate Soccer Players" (The Amer. J. of Sports Medicine, 2002, p. 157-162) investigaram esta questão a partir de várias perspectivas.
a. artigo informou que 45 dos 91 jogadores de futebol em sua amostra sofreram pelo menos uma concussão, 28 de 96 atletas não-jogadores de futebol sofreram pelo menos uma concussão, e apenas 8 de 53 estudantes revelaram o mesmo quadro. Analise este dado e tire as conclusões apropriadas.
b. Para os jogadores de futebol, o coeficiente de correlação da amostra calculado a partir dos valores de exposição do jogador (número total de temporadas jogadas antes de inscrever-se no estudo) e classificação em um teste de memória imediata foi . Interprete este resultado. foi . Interprete este resultado.
c. Aqui está um resumo das informações sobre classificações em um teste de associação de palavras oral controlado para jogadores de futebol e atletas não jogadores de futebol:
,
d. Analise este dado e tire as conclusões apropriadas.Considerando o número de concussões anteriores em não-jogadores de futebol, os valores da média ± desvio padrão para os três grupos foram 0,30 ± 0, e . Analise estes dados e tire as conclusões apropriadas.
Passo 1
E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:
artigo informou que 45 dos 91 jogadores de futebol em sua amostra sofreram pelo menos uma concussão, 28 de 96 atletas não-jogadores de futebol sofreram pelo menos uma concussão, e apenas 8 de 53 estudantes revelaram o mesmo quadro. Analise este dado e tire as conclusões apropriadas.
a. Nossas hipóteses são : não há diferença na proporção de concussões entre os três grupos. : há uma diferença ...
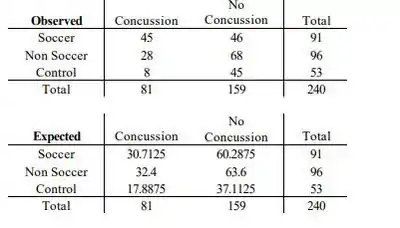
.
O df para este teste é (I-1)(J-1) =2, então rejeitamos se , então rejeitamos . Há uma diferença na proporção de concussões com base no fato de uma pessoa jogar futebol.
Passo 2
Para os jogadores de futebol, o coeficiente de correlação da amostra calculado a partir dos valores de exposição do jogador (número total de temporadas jogadas antes de inscrever-se no estudo) e classificação em um teste de memória imediata foi . Interprete este resultado. foi . Interprete este resultado.
b. Estamos testando a hipótese? 0. A estatística de teste é. No nível de significância α=0,01, falharíamos em rejeitar e concluir que não há evidência de correlação diferente de zero na população. Se estivéssemos dispostos a aceitar um nível de significância mais alto, nossa decisão poderia mudar. Na melhor das hipóteses, há evidências de apenas uma correlação fraca.
Passo 3
c. Vamos testar para ver se a pontuação média em um teste de associação de palavras controlada é a mesma para atletas de futebol e não futebol. vs . Usaremos a estatística de teste
. With e , O
O valor de p será >.10, portanto não rejeitamos e concluímos que não há diferença na pontuação média no teste para os dois grupos de atletas.
Passo 4
Nossas hipóteses para ANOVA são : todas as médias são iguais vs : nem todas as médias são iguais. A estatística de teste
. Usando df 2.200 da tabela A.9, o valor p está entre 0,01 e 0,05. Ao nível de significância 0,05, rejeitamos a hipótese nula. Há evidências suficientes para concluir que há uma diferença no número médio de concussões anteriores não relacionadas ao futebol entre os três grupos.
Resposta
a. Há uma diferença na proporção de concussões com base no fato de uma pessoa jogar futebol.
b. Na melhor das hipóteses, há evidências de apenas uma correlação fraca
c. O valor de p será >.10, portanto não rejeitamos e concluímos que não há diferença na pontuação média no teste para os dois grupos de atletas.
d. Há evidências suficientes para concluir que há uma diferença no número médio de concussões anteriores não relacionadas ao futebol entre os três grupos.
Espero que tenham aprendido com essa questão, até a próxima !