Exercícios de Algumas funções úteis – Parte 2 - Lista de Exercícios Resolvida

Acredita-se que a resistência à tensão da borracha siliconizada seja uma função da temperatura de cura. Um estudo foi realizado, no qual amostras de 12 espécimes de borracha foram preparadas usando temperaturas de cura de 20 °C e 45 °C. A tabela abaixo mostra os valores de resistência à tensão, em megapascals, para cada temperatura:

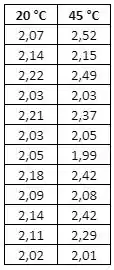
Usando o MATLAB, responda às seguintes questões:

1. Qual a média de resistência à tensão de cada amostra?
2. Qual é o desvio padrão de resistência à tensão para cada temperatura? O aumento de temperatura parece influenciar a variabilidade de resistência à tensão?
3. Em estatística, a amplitude é a diferença entre o maior e o menor valor de um conjunto de dados. Para cada temperatura, qual é a amplitude de resistência à tensão?

Considere o corpo rígido abaixo, que possui três graus de liberdade rotacionais:

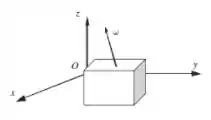
A matriz de momentos de inércia do corpo rígido tem a forma:

onde os momentos de inércia, em kgm², são definidos de acordo com o sistema de coordenadas .

É possível determinar um novo sistema de coordenadas, com eixos ortogonais, de forma que a matriz seja diagonal. Esses eixos ortogonais do novo sistema de coordenadas são chamados de eixos principais, e os momentos de inércia associados a eles são chamados de momentos de inércia principais. Os momentos de inércia principais são dados pelos autovalores de e os eixos principais, pelos autovetores de . Com o MATLAB, determine os eixos principais e os momentos de inércia principais para a matriz .

Passo 1

A questão nos mostra a matriz de momentos de inércia de um corpo rígido e nos pede para encontrarmos os eixos principais e os momentos de inércia principais a partir de . Os eixos principais são os autovetores de e os momentos de inércia principais são os autovalores de . Este exercício é resolvido usando a função eig() do MATLAB, que nos dá os autovalores e os autovetores de uma matriz.

Passo 2

Primeiramente, entramos a matriz no Command Window do MATLAB usando o código:

I_rot = [150 0 -100;0 250 0;-100 0 500]

Em seguida, usamos a função eig(), tendo I_rot como entrada, entrando com o comando:

[dir_princ,mom_princ] = eig(I_rot)

Nesse comando, pedimos ao MATLAB que encontre os autovetores e os autovalores da matriz I_rot. Os autovetores são armazenados na variável dir_princ e os autovalores, na variável mom_princ. No Command Window do MATLAB, fica assim:

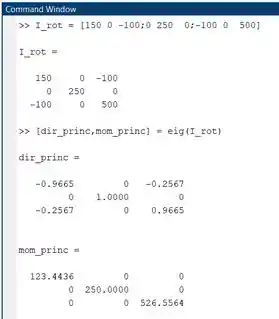
Os autovetores de I_rot são as colunas da matriz dir_princ. Logo, os eixos principais são definidos pelos vetores:

Os autovalores de I_rot são os elementos da diagonal principal da matriz mom_princ. Logo, os momentos de inércia principais são:

123,4436 kgm²

250 kgm²

526,5564 kgm²

Resposta

Os eixos principais definidos a partir de são representados pelos vetores:

Os momentos de inércia principais definidos a partir de são:

123,4436 kgm²

250 kgm²

526,5564 kgm²

Na definição de autovalores e autovetores, temos que, dada uma matriz quadrada A:

onde V é uma matriz cujas colunas correspondem aos autovetores e D é uma matriz diagonal, em que os elementos da diagonal principal são os autovalores da matriz A.

Usando o MATLAB, dada a matriz:

1. Encontre os autovalores e os autovetores de A;
2. Verifique a igualdade .

Três amigos prestaram um vestibular e as notas que eles tiraram em cada disciplina são apresentadas na tabela abaixo:

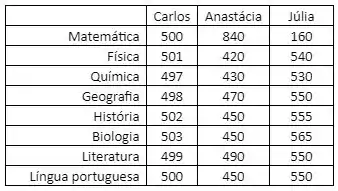
Usando o MATLAB, responda as seguintes perguntas:

1. Qual dos três teve a maior nota média?
2. Qual dos três apresentou menor variação de desempenho em relação à média de notas nas disciplinas?

A tabela abaixo apresenta os dados de uma curva de torque de um motor à combustão.

Com o MATLAB, encontre o torque máximo e determine a velocidade em que o motor atinge o torque máximo.

Considere um motor a pistão em uma aeronave. Durante o seu funcionamento, um sensor de temperatura registrou os seguintes dados:

Determinar o valor máximo, mínimo e médio da temperatura em graus Celsius.

O adaptador para redução de ruído é um equipamento utilizado para reduzir o efeito de interferência de ruídos em um sinal. Por exemplo, um microfone que é utilizado para gravar sinais de voz de um grande auditório. Outro microfone é usado na parte de trás do auditório para colher principalmente os sinais de ruído. Através das técnicas para cancelamento de ruídos, as características do sinal de ruído podem ser determinadas usando o sinal de dois microfones. Os adaptadores são utilizados para reduzir o ruído oriundo da parte de trás do auditório, para poderem ser transmitidos para a sala de controle. Este processo resulta num sinal limpo e uma melhor comunicação.

Os algoritmos para os adaptadores estão acima do nível deste texto, mas a performance e a velocidade do algoritmo dependem das características dos sinais de entrada. Estas características determinam a superfície multidimensional quadrática para que obtenhamos um valor mínimo. Este mínimo é determinado ajustando o algoritmo para um ponto de partida para um único mínimo. Se a superfície quadrática tem um contorno circular, o algoritmo não é necessário. A matriz pode ser computada a partir dos sinais de entrada, e os autovalores da matriz irão determinar o tipo de superfície de contorno a ser utilizada. Se os autovalores forem iguais, a superfície é circular. Quanto maior a variação dos autovalores, mais elíptica será a superfície. Os autovetores representam o eixo principal da superfície. Portanto para determinar a velocidade e a performance do algoritmo do adaptador com certeza do tipo de dados e para analisar a superfície, nós precisamos determinar os autovalores e autovetores da matriz .

Escreva um programa para ler os valores da matriz , e depois calcule os autovalores e autovetores.

Use o comando seguinte para criar uma matriz chamada :

1. Calcule a média de cada coluna e atribua o resultado a um vetor .
2. Calcule o desvio padrão de cada coluna e atribua o resultado a um vetor .