Criação de polinômios
Teoria
Opa iae, tudo em cima?
Hoje iremos começar um novo bloco de conteúdos: os polinômios.
Bem, os polinômios são expressões matemáticas encontradas frequentemente na modelagem e na solução de problemas nas engenharias e demais ciências exatas.
Vamos imaginar que você é um engenheiro dedicado e deseja estudar a variação da temperatura ao longo do tempo em um reator, e experimentalmente foram obtidos os seguintes dados:
Aí teu chefe chega para tu e pergunta “Em quanto tempo o reator chegará na temperatura crítica de ?”
Só olhando os pontos fica complicado né? Mas e se nós tivéssemos uma função que relacionasse tempo e temperatura, que pudesse te dar uma ideia desses valores?
Muito mais fácil de predizer algo né?
Pois bem, vamos aprender a criar essas funções!
Beeeeem, no Matlab existem duas formas de criar um polinômio, a primeira forma é inserindo os coeficientes do polinômio manualmente e a segunda é o que nós usaremos pra resolver o exemplo anterior, onde queremos gerar um polinômio a partir de alguns pontos já dados.
E adivinha... são esses métodos que iremos ver hoje!
Primeiro Método
O primeiro método para criação de um polinômio em matlab é escrevendo diretamente no programa, mas como fazer isso né?
Vaaaaamos voltar para aqueles exemplos básicos de cálculo, imagine que você tem a seguinte função de segundo grau:
Se nós analisarmos direitinho, podemos organizar a função da seguinte maneira:
Opa, organizamos nosso polinômio como uma multiplicação entre dois vetores, sabe qual é o bom disso?
Para criar um polinômio no Matlab, basta inserirmos um vetor com os coeficientes do polinômio:
Temos algumas funções no Matlab que trabalham especificamente com polinômios e quando inserimos numa delas um vetor desse tipo, automaticamente elas interpretam que esses valores são os coeficientes de um polinômio e realizam as operações desejadas.
Ah e uma coisa, por exemplo se tivéssemos o seguinte polinômio:
Reescrevendo na forma de vetores, fica:
Mas como iremos inseri-lo no Matlab?
Bem, em casos como esse, onde temos um coeficiente nulo (igual a ), vamos formular o polinômio da seguinte forma:
Pois quando o valor zero multiplicar o , ele irá sumir do polinômio, beleza?
Então o polinômio no Matlab fica:
E como essas informações me ajudam? E se eu quiser calcular o valor do polinômio pra um determinado ?
Basta utilizar uma outra função chamada !
Então vamos calcular o valor do polinômio quando . Olha como fica o código:
Primeiramente, vamos inserir o vetor do polinômio:
Depois disso vamos implementar a função , para calcular o valor do polinômio.
A função no Matlab se torna:
A sintaxe exige os coeficientes do polinômio na primeira variável enquanto a segunda variável é o valor de que se deseja calcular o polinômio.
O código do Matlab fica assim:
Executando o código geramos os seguintes resultados:
Prontinho! Vamos pro segundo método!
Segundo Método: Interpolação Linear
O segundo método para criação de um polinômio é criá-lo a partir de dois vetores de dados numéricos, um que corresponde às variáveis que conhecemos por variáveis dependentes e outro que conhecemos pelas variáveis independentes.
Ok, oook na sua cabeça deve estar se perguntando “mas como se cria isso?”
Vamos responder isso com um exemplo, belezinha? Então vamos lá
Aproveitando os dados do exemplo lá do comecinho, vamos criar primeiramente os vetores de entrada de dados.
Para lembrarmos dos dados, a tabela é a seguinte:
Agora vamos inserir o vetor das variáveis independentes:
Agora vamos inserir o vetor das variáveis dependentes, ou seja, aquelas variáveis que dependem de .
Agora que criamos os vetores precisamos criar o polinômio.
Para isso, vamos fazer uma regressão polinomial, essa ferramenta que cria uma função polinomial que ajusta a própria função para predizer o máximo possível os vetores que foram informados.
No Matlab essa função se chama , e sua sintaxe para o exemplo em questão é dada por:
Seu código deve ficar algo mais ou menos assim:
Executando o código você irá encontrar o seguinte vetor:
E essa é a função de primeiro grau que se ajusta aos vetores numéricos, logo:
Mas onde falamos que o polinômio é de primeiro grau né?
Voltando à função , se você olhar direitinho existe um local na sintaxe que colocamos o número É justamente aí que você vai indicar qual o grau do polinômio que você quer, entende?
Vamos colocar o número nesse lugar e ver o que acontece, belezinha? Olha só o que vai mostrar:
Um novo coeficiente, ou seja, um polinômio de segundo grau:
Mas como eu vou saber se o polinômio realmente se ajusta bem aos pontos?
Beeeeeeem a forma mais simples é plotando o gráfico com os valores dos vetores.
Para isso precisamos adicionar mais algumas linhas ao nosso código okay?
Primeiramente vamos criar um vetor de pontos para representar o vetor de uma forma contínua:
Agora vamos calcular o valor do polinômio nesses pontos utilizando a função
Agora iremos criar um plot para a saída de dados:
O seu código completinho deve ficar algo mais ou menos assim:
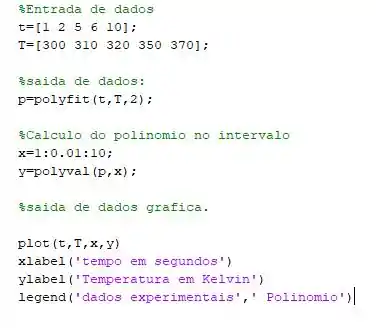
Executando o código, deverá ser gerado um gráfico mais ou menos assim:
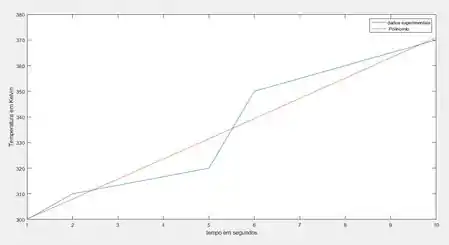
Iae o que achou? Ferramentas interessantes para engenharia né?
Beeeeeeeeeem, vamos ficar por aqui pessoal. Mas não esqueça de olhar os exercícios para praticar, selecionamos uns exercícios bem da hora para vocês!
Eeeeeeeeee até a próxima!
Segundo Método: Interpolação Linear
Exercícios Resolvidos
Exercício Resolvido #1
“Elaboração Própria”
Plote o polinômio:
No domínio . Primeiramente crie um vetor. Em seguida, utilize a função para terminar os valores de e por fim, empregue a função .
Passo 1
A questão quer que a gente plote o gráfico de um polinômio utilizando a função , pois pede para calcular o valor do polinômio sob todos os valores dentro do intervalo dado.
Se temos um intervalo é mais simples trabalhar operações sobre vetores pois temos infinitos números dentro daquele intervalo. Uma vez que criamos o vetor com os elementos daquele intervalo que foi dado (em x), podemos calcular a função sob o vetor para ter todos os seus valores (em y). Para uma melhor visualização, vamos plotar os resultados em uma imagem gráfica.
Então o algoritmo para a resolução desse problema é o seguinte:
1-Entrada de dados – Criação do vetor X e do polinômio na forma vetorial
2- Cálculo do polinômio utilizando a função
3-Gerar o gráfico com o comando plot.
Passo 2
Primeiramente vamos inserir os coeficientes do polinômio.
Lembrando que os termos que não aparecem no polinômio, nós trocamos por 0 no vetor, então como não aparece a potência cúbica, o polinômio fica assim:
A justificativa de ficar assim é a mesma mostrada em aula, utilizando álgebra básica podemos mostrar que o polinômio da questão pode ser obtido através da multiplicação das seguintes matrizes:
E os coeficientes correspondem justamente a matriz .
Agora vamos criar o Vetor .
o incremento foi escolhido 0.1 de forma arbitrária para conter o maior número possível de elementos que correspondam aos valores do intervalo fornecido na questão.
Agora vamos inserir a função para o cálculo dos polinômios:
Uma vez que criamos as funções vamos gerar a saída de dados que corresponde a:
Passo 3
O código em Matlab deve ficar algo mais ou menos assim:
Executando o código iremos obter o seguinte resultado:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
“Elaboração Própria”
Considere os polinômios abaixo, programe os polinômios abaixo em Matlab e calcule seu valor no ponto que se pede.
- , Calcule o valor da para
- , Calcule o valor da para
- , Calcule o valor da para
Passo 1
A questão em si é uma questão de aplicação bem simples, onde basicamente a questão quer praticar a aplicação das novas ferramentas para criação e cálculo de polinômios.
A atividade é composta de duas partes: a primeira parte é implementar os coeficientes dos polinômios, já a segunda é realizar o cálculo dos polinômios no valor desejado.
logo, o algoritmo primeiramente vai inserir os vetores dos coeficientes, uma vez que já programamos os coeficientes, precisamos apenas calcular o valor do polinômios utilizando a função
sendo assim, o algoritmo é algo mais ou menos assim:
- Entrada de dados: aqui vamos inserir os valores dos polinômios de cada alternativa:
- Cálculo dos polinômios utilizando a função
- Gerar uma saída de dados organizada anexando tal valor do polinômio a sua alternativa correspondente.
Passo 2
Transformando o algoritmo em programação no Matlab vamos inserir os seguintes pontos:
Primeiramente vamos inserir os coeficientes do polinômio:
Lembrando que os termos que não aparecem no polinômio nos trocamos por 0 no vetor, então os polinômios ficam algo assim:
Agora vamos inserir a função para o cálculo dos polinômios:
Uma vez que criamos as funções vamos gerar a saída de dados que corresponde a:
O código em Matlab deve ficar algo mais ou menos assim:
Executando o código iremos obter os seguintes resultados:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
“Elaboração Própria”
Um aluno realizou um experimento onde colocava um certo bloco em cima de uma mesa para calcular o efeito que a massa tinha na compressão das pernas da mesa.
Devido a repetidos experimentos ele obteve os seguintes dados experimentais:
Utilize os dados experimentais para encontrar o polinômio que melhor se ajusta aos dados experimentais.
Passo 1
A questão é uma aplicação direta do segundo método para criação de polinômios, ele deu dois vetores de dados e pede para encontrar o polinômio que melhor se ajuste aos dados experimentais.
Para isso iremos precisar criar um código que além de gerar a função também gere uma saída de dados gráfica para que possamos comprar os dados com o polinômio para ver se a curva realmente se ajusta bem:
Para isso vamos realizar o seguinte algoritmo:
- Entrada de dados ( inserir os vetores dado da questão)
- Programação do ajuste utilizando a função
- Criação de uma saída de dados para comprar o polinômio com os dados experimentais.
Passo 2
Transformando o algoritmo em programação no Matlab vamos inserir os seguintes pontos:
Primeiramente vamos inserir vetores de dados:
Agora vamos inserir a função para o cálculo do polinômio:
Uma vez que criamos as funções vamos gerar a saída de dados que corresponde a criação dos seguintes elementos de código:
Criação de um vetor para a variação contínua da curva e a criação da própria curva:
Agora vamos criar o plot:
O código em Matlab deve ficar algo mais ou menos assim:
Após variar a ordem do polinômio foi visto que o polinômio que melhor se ajusta com menor ordem possível é o polinômio de grau 3, sendo assim o gráfico do polinômio de grau 3 fica:
Cujo os coeficientes são dados pelos seguintes valores:
Resposta
O polinômio que melhor se ajusta é o polinômio:
Exercício Resolvido #4
“Exercício adaptado da página 252 do livro Matlab com aplicações a engeharia- Amos gilat”.
A equação de estado do gás ideal ela relaciona volume, pressão, temperatura e quantidade molar através da seguinte expressão:
Onde R, V, P e T são respectivamente a constante universal dos gases, volume, pressão e temperatura do gás.
Em um experimento um aluno de engenharia confinou em um reservatório 0.05 mol de gás em um recipiente, ao aquecer o gás observou a variação da pressão e do volume conforme a temperatura aumentava, gerando os seguintes dados:
Utilize os dados fornecidos para ajustar um polinômio de primeiro grau de V em função de
E assim caracterize o valor da constante universal dos gases e compare com os valores da literatura para justificar se o ajuste foi válido.
Passo 1
A questão é uma aplicação quase direta do segundo método para criação de polinômios, ele deu três vetores de dados e pede para encontrar o polinômio que melhor se ajuste aos dados experimentais.
Mas antes de irmos para o código precisamos primeiramente regredir de 3 vetores para 2, para assim poder fazer o ajuste linear, então o algoritmo fica:
- Entrada de dados ( inserir os vetores dado da questão)
- Cálculo do
- Programação do ajuste utilizando a função
- Criação de uma saída de dados para comprar o polinômio com os dados experimentais.
Passo 2
Transformando o algoritmo em programação no Matlab vamos inserir os seguintes pontos:
Primeiramente vamos inserir vetores de dados e colocando a temperatura em kelvin:
Agora vamos criar o vetor X, lembrando que vamos dividir elemento a elemento:
Agora vamos inserir a função para o cálculo do polinômio:
Uma vez que criamos as funções vamos gerar a saída de dados que corresponde a criação dos seguintes elementos de código:
Criação de um vetor para a variação contínua da curva e a criação da própria curva:
Agora vamos criar o plot:
O código em Matlab deve ficar algo mais ou menos assim:
Executando podemos obter os seguintes resultados:
Cujo os coeficientes são dados pelos seguintes valores:
Resposta
Encontramos com o ajuste um valor de e a literatura(google) informa:
Então o nosso ajuste conseguiu prever com eficiência o valor da constante universal dos gases.
Exercício Resolvido #5
“Exercício Adaptado do livro Matlab com Aplicações à Engenharia - Amos Gilat”.
O limite de escoamento de muitos metais depende do tamanho das partículas. Para esses metais, a relação entre o limite de escoamento e o diâmetro médio das partículas pode ser modelada pela equação de Hall-Petch conforme mostrado abaixo:
Através de ensaios experimentais foram obtidos os seguintes resultados:
Utilize os dados experimentais e calcule o valor de e de
Passo 1
A questão nos deu dois vetores de dados e pede para encontrarmos o valor das constantes correspondentes na fórmula dada.
Pra resolver, precisamos usar o método de interpolação linear através da função para encontrar o polinômio que melhor se ajusta aos dados experimentais. Uma vez que conseguimos encontrar esse polinômio, por comparação vimos que o coeficiente linear corresponde ao enquanto o coeficiente angular corresponde ao .
Mas você talvez tenha reparado que na tabela temos o diâmetro , enquanto a fórmula tem esse termo dentro de uma raiz . Será que isso dá problema nos nossos cálculos?
Olha só, se em vez de ajustarmos em função de diretamente, nós calcularmos a raiz em cada ponto e ajustarmos em função de , dá tudo certo!
Então é isso que iremos fazer e o algoritmo fica algo mais ou menos assim:
- Entrada de dados (inserir os vetores dado da questão)
- Cálculo do
- Programação do ajuste utilizando a função
- Criação de uma saída de dados para comprar o polinômio com os dados experimentais.
Passo 2
Transformando o algoritmo em programação no Matlab vamos inserir os seguintes pontos:
Primeiramente vamos inserir vetores de dados:
Agora vamos criar o vetor X que é calculado pela seguinte expressão:
Agora vamos inserir a função para o cálculo do polinômio:
Nessa função, os dois primeiros termos dentro dos parênteses representam o conjunto de dados que serão ajustados, no nosso caso em relação a , e por último vem o termo que indica o grau do polinômio que será gerado, no nosso caso .
Passo 3
Uma vez que criamos as funções vamos gerar a saída de dados que corresponde a criação dos seguintes elementos de código:
Como vamos criar um gráfico, vamos criar um vetor no mesmo intervalo dos pontos do eixo com muitos pontos para gerar uma curva contínua:
Agora, precisamos calcular o valor correspondente do polinômio a cada um dos valores de que definimos, pra isso usamos a função .
Nela, o primeiro termo representa os coeficientes do polinômio e são dados pelo que calculamos com a função , enquanto o segundo termo é o valor ou conjunto de valores que vão entrar nesse polinômio, no nosso caso é o vetor que acabamos de definir:
Agora vamos criar dois plot juntos, o primeiro com os valores de e que usamos para encontrar o polinômio e o segundo com os valores de e que representam a reta que encontramos através da interpolação linear:
O código completo em Matlab deve ficar algo mais ou menos assim:
E gerando o seguinte gráfico:
Cujo os coeficientes são dados pelos seguintes valores:
Resposta
Analisando os coeficientes obitidos pelo ajuste dos dados experimentais podemos concluir que:
Exercício Resolvido #6
Autoria própria
Dados os polinômios:
A soma é igual a?
Passo 1
Aqui temos uma questão bem padrão de polinômios, o enunciado pede para calcular o valor do polinômio para o valor de e seguidamente pede para calcularmos o valor de para valor de e finalmente somar esses valores para ter o resultado final.
Para resolver a questão primeiramente precisamos inserir os vetores dos coeficientes de cada polinômio. Uma vez que implementamos, vamos utilizar a função que é uma função que serve para calcular os valores dos polinômios para algum valor de
Sendo assim, o algoritmo do nosso programinha ficaria:
1-Implementação dos vetores dos coeficientes dos polinômios P e Q
2-Cálculo dos polinômios nos valores especificados de X
3-Cálculo da soma de P e Q
Passo 2
Agora que já montamos nosso algoritmo vamos implementá-lo na forma de código no Matlab.
Nossa primeira linha será composta pelos vetores dos coeficientes dos polinômios P:
Lembrando que o apareceu simplesmente porque não tem o coeficiente do no polinômio P, por isso colocamos o valor nulo quando vamos implementar no Matlab.
De forma similar temos o polinômio Q:
Passo 3
Agora que implementamos os coeficientes dos vetores precisamos apenas calcular os valores dos polinômios com a função polyval. Primeiro entramos com o polinômio e depois o valor de x.
Agora vamos implementar a função da soma para assim resolver a questão em sí:
Passo 4
Resultado o seguinte codigozinho:
Executando o código:
Resposta
Executando o código você irá encontrar os seguintes valores para o polinômio e consequentemente a soma:
Exercício Resolvido #7
IFB-2017
Em relação a função podemos afirmar que:
- Não tem raízes reais
- Tem cinco raízes reais
- Tem três raízes reais e duas complexas
- Tem uma raiz real e quatro complexas
- Tem duas raízes reais e três complexas
Passo 1
Aqui temos uma questão bem padrão de polinômios, o enunciado pede para encontrar a afirmativa correta em relação às raízes do polinômio informado na questão.
Para realizar isso precisamos encontrar as raízes desse polinômio. Por sorte, o Matlab tem a função roots para que possamos calcular essas raízes.
Primeiramente iremos precisar implementar os vetores dos coeficientes do polinômio da questão, após isso iremos usar a função para calcular as raízes do polinômio e assim analisar as alternativas da questão.
Sendo assim, o algoritmo para resolução do problema se torna:
1-Implementação do vetor com os coeficientes do polinômio
2-Utilização da função roots
3-Analisar os resultados
Passo 2
Primeiramente vamos implementar o vetor dos coeficientes do polinômio informado na questão.
Lembrando que esses entraram no vetor pois não aparece e no polinômio da questão, o que corresponde ao coeficiente 0 multiplicando eles.
Agora iremos encontrar as raízes do polinômio através da função .
O codigozinho deverá ficar assim:
Executando o código, iremos encontrar as seguintes raízes:
Resposta
Analisando as repostas obtidas pelo Matlab conseguimos notar aparentemente que temos 5 raízes complexas, mas se olharmos a última raiz o coeficiente do é .
Então temos que a última raiz não é complexa, logo temos 4 raízes complexas e 1 raiz real correspondendo a alternativa D.
Exercício Resolvido #8
Autoria própria
Considere o tanque de água que se mostra na figura seguinte:
Para estudar o sistema abriu a torneira e recolheram-se valores da altura da água durante os 10 primeiros minutos, como mostrado na tabela abaixo:
Encontre a curva que melhor se ajusta a esses dados experimentais e preveja o valor da altura após 12 min.
Passo 1
Opa galera, aqui temos uma questão de ajuste experimental que na realidade é apenas um nome bonito que a universidade dá quando quer ajustar um polinômio ou uma função qualquer a um conjunto de números.
Aqui queremos encontrar uma um polinômio que melhor se ajuste aos dados de altura de líquido que foram medidos com o passar do tempo.
Para isso vamos utilizar a função para encontrar o polinômio que melhor se ajuste aos dados experimentais.
Passo 2
Primeiramente para realizar o ajuste precisamos implementar os vetores de dados dentro do Matlab:
Agora iremos chamar a função polyfit e também vamos inserir uma janela gráfica para verificar se a função realmente está se ajustando bem aos dados.
Sendo assim a função polyfit precisa de três argumentos: o primeiro são os dados da variável ; o segundo são os dados da variável ; e finalizamos inserindo o grau do polinômio para ajustar.
Nós vamos ajustar um polinômio de grau 2, pois ele já demonstra ser um bom ajuste como mostraremos depois.
Sendo assim, temos:
Para plotar precisamos calcular os valores desse novo polinômio, então vamos criar um vetor auxiliar variando de 0 até 12.
Onde sua utilidade é apenas para usar o com os coeficientes que vamos calcular com a função , gerando as seguintes linhas de código:
E vamos finalizar com a função plot, para podermos visualizar se o ajuste realmente está bom.
Passo 3
Ao executar o código que acabamos de montar geramos o seguinte polinômio:
Onde podemos gerar a seguinte curva:
Aqui podemos observar que o ajuste foi consideravelmente bom.
Agora vamos calcular o valor de altura para 12 min, temos que o polinômio nos fornece um valor igual a:
Resposta
O polinômio que teve o melhor ajuste foi um polinômio de grau 2 e o valor da altura em 12 min é uma altura de 6.0509 metros.