Múltiplos gráficos em uma janela de saída.
Produzido por Gustavo BarbosaTeoria
Alguns tópicos teóricos
Iae ta tudo bem?
Hoje vamos conversar quando queremos gerar mais de um gráfico em uma saída de dados, para começar a falar sobre esse problema em questão vamos primeiro resolver um exemplo simples ok?
Primeiramente iremos implementar o vetor de entrada:
Agora iremos calcular as funções de entrada e saída do nosso problema
Agora iremos plotar os gráficos com os determinados valores
Se você escreveu tudo certinho o seu código deve ser algo mais ou menos assim:

Só que ao executar apareceu um problema né?
Que deixa eu adivinhar, no caso seu código só conseguiu plotar a curva do seno?
Não sei se você lembra, mas o Matlab é uma linguagem interpretada, ou seja, ele sai lendo e executando linha a linha da sua rotina.
Só que quando chega na função plot, ele primeiramente plota o cosseno, porém, quando vai para plotar o seno ambas as figuras estão indicadas que estão na mesma janela gráfica, ou seja, o Matlab plota o Cosseno e depois ele escreve o gráfico do Seno por cima do cosseno.
Revelando apenas o gráfico do seno no final.
É bem comum em problemas de engenharia precisarmos resolver problemas onde precisamos de mais de um gráfico e muitas vezes não podemos inserir as duas curvas num gráfico só.
Por exemplo, imagine que você está estudando a taxa de aquecimento e o perfil de temperatura de uma placa variando ao longo do comprimento de uma cerâmica quadrada.
Você não pode plotar no eixo Y o perfil de temperatura e a taxa de aquecimento, porque ambas são grandezas distintas, logo seu gráfico ficaria sem sentido.
Mas como resolvo isso né? Calminhaaa esse é o assunto que iremos estudar hoje.
Temos basicamente duas funções específicas para resolver esse problema, a função e a função
A diferença entre elas é simples, a função figure cria outras janelas gráficas e a função subplot permite colocar mais de um gráfico em uma única janela.
Opa ficou complicado né? Vamos ver elas separadamente, ok?
Função figure
A função figure é uma função que cria uma nova janela gráfica, vamos retornar ao exemplo anterior e ver como fica?
O início do programa não muda em nada, ok?
Sendo assim, o início dele ficará assim:
O que iremos modificar é que iremos inserir cada plot em uma janela gráfica diferente, portanto, o primeiro plot ficará na janela gráfica 1, deixando seu código dessa forma:
E consequentemente o segundo gráfico ficará na segunda janela gráfica:
Portanto, sua rotina deverá ficar algo mais ou menos assim:

Executando o código teremos os seguintes gráficos:
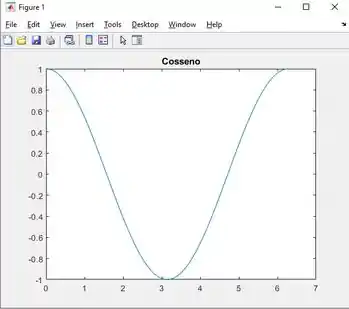
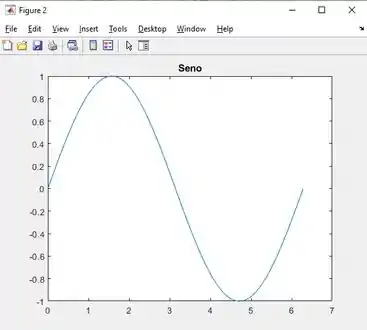
Iae vamos para a próxima função? Ela é o subplot, particularmente acho ela mais legal.
Função Subplot
O comando subplot divide a janela gráfica em uma matriz de gráficos, geralmente esse comando é bastante útil quando queremos tirar informações sobre múltiplos gráficos,
Retornando ao exemplo anterior vamos criar um subplot dos gráficos okay?
Sem se preocupar com a sintaxe no momento vamos fazer o seguinte:
No lugar da função coloque
E no lugar da função coloque
Deixando sua rotina assim:

Aqui claramente podemos ver informações como, nos pontos onde o cosseno é 0, o seno alcança os valores de .
Mas o que o subplot fez né? Ele pegou duas janelas gráficas e se unificou em uma matriz de uma coluna e duas linhas.
Mas o que a sintaxe significa? Vamos lá
m – esse valor vai indicar o número de linhas que sua “matriz gráfica” vai ter, nesse exemplo em questão temos dois gráficos e escolhemos por .
n – esse valor indica quantas colunas nossa “matriz gráfica” vai ter, por exemplo como escolhemos que o número de linhas é 2, como temos dois gráficos só sobra para n o valor 1.
p – aqui é o tchan do subplot, esse valor indica qual gráfico entra no subplot. Por exemplo no primeiro gráfico o p foi igual a 1, para indicar que ele é o primeiro gráfico. Já o segundo gráfico o p foi igual a 2 para indicar que ele é o segundo gráfico.
mas e se invertermos os valores de m e n né?
Vamos lá, coloque m=1 e n=2 no seu código, o seu subplot deverá ficar algo assim:

Ou seja, saímos de uma matriz de coluna para uma matriz de linha, sacou?
Opa galera, vamos ficar por aqui e não esqueça de dar um pulinho nos exercícios, pois eles foram selecionados para você praticar e ficar showcesso nesse conteúdo ok?
Então até mais.
Função figure
Função Subplot
Exercícios Resolvidos
Exercício Resolvido #1
“Elaboração Própria”
Elabore em Matlab uma rotina que consiga plotar os gráficos das funções seno, cosseno e tangente variando de até em uma única janela gráfica.
Passo 1
A questão em si é uma questão simples da aplicação da ferramenta subplot, para isso precisamos escrever o código para calcular as funções e depois gerar os gráficos em uma única janela gráfica.
Primeiramente, vamos escrever o algoritmo para a resolução do problema.
1 - Entrada de dados: criação do vetor ângulo
2 - Cálculo funções do problema
3 -Criação dos gráficos com o subplot
Passo 2
Uma vez que criamos o algoritmo iremos agora implementar o código no Matlab.
Primeiramente iremos criar o vetor ângulo:
Agora iremos calcular as funções no Matlab:
Uma vez que calculamos as funções, iremos criar os plots e em seguida iremos organizá-los:
Vamos utilizar o subplot e criar uma matriz coluna, pois temos 3 funções e cada um irá retornar um gráfico diferente, sendo assim o gráfico do cosseno fica:
O seno por sua vez irá ocupar o segundo gráfico, então:
E finalmente terceiro gráfico será ocupado pela tangente
Sendo assim seu código irá se tornar:

Passo 3
Executando o código iremos obter o seguinte gráfico:
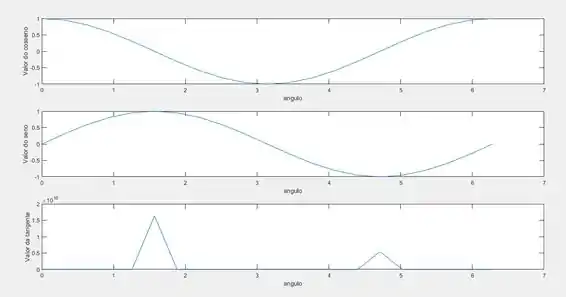
Aqui podemos notar que em locais onde o cosseno é zero a tangente ela assume valores tendendo ao infinito como se esperado pois por definição a tangente é inversamente proporcional ao cosseno, ou seja quanto mais o cosseno diminui mais a tangente cresce.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
“Elaboração Própria”
A posição de uma partícula ao longo do tempo pode ser descrita pelas seguintes equações:
Escreva uma rotina em Matlab na qual plote todos os três gráficos em uma janela gráfica só.
Passo 1
A questão apresenta as equações que descrevem um movimento de uma partícula ao longo do tempo e pede para que escreva uma rotina que gere os três gráficos do movimento da partícula em uma janela gráfica só.
A função que realiza isso se chama subplot e é ela que iremos utilizar para resolver o problema.
Primeiramente precisamos compor o algoritmo do programa para termos uma ideia de como o programa irá se desenvolver.
1-Entrada de dados: criação do vetor tempo
2-Cálculo das equações do movimento
3-criação dos gráficos com o subplot
Passo 2
Uma vez que criamos o algoritmo iremos agora implementar o código no Matlab.
Primeiramente iremos criar o vetor tempo:
As funções que o enunciado deu são contínuas, mas o que nós vamos plotar são vetores, ou seja, essas funções vão estar discretizadas. Então o nosso tempo também vai estar discretizado. Eu escolhi fazer um bem pequeno pra melhorar a precisão do gráfico e colocar a escala até 100, mas como o enunciado não especificou, você pode usar outros valores.
Agora iremos calcular as funções no Matlab:
Aqui devemos lembrar que iremos executar as operações ponto a ponto dentro do vetor tempo, então antes de cada operação precisamos inserir o “.” Ok?
Agora que calculamos as funções, vamos criar os plots e em seguida iremos organizá-los.
Passo 3
Para programar a função subplot vamos precisar de três índices, o primeiro índice vai dizer quantas linhas de gráficos vai ter na janela gráfica.
Como temos 3 gráficos, vamos imprimir uma janela gráfica com os gráficos um abaixo do outro, ou seja, iremos precisar de 3 linhas, fazendo com que o primeiro índice seja 3.
O segundo índice é o número de colunas de gráficos que vamos criar na janela, como vamos imprimir em 3 linhas não temos mais gráficos para imprimir, logo vamos precisar apenas de 1 coluna fazendo com que o segundo índice seja igual a 1.
O último índice da função subplot indica a posição que o gráfico vai se posicionar, por exemplo, se eu quiser imprimir o gráfico como o primeiro, o subplot fica:
Se caso eu escolhesse ele na segunda posição, o seu subplot ficaria:
e assim sucessivamente.
Conforme o que foi mostrado, iremos chamar o subplot e criar uma matriz coluna, a posição irá compor o primeiro gráfico logo o seu subplot se torna:
O gráfico da velocidade irá ocupar o segundo gráfico, então:
E o terceiro gráfico será ocupado pela aceleração
)
Sendo assim seu código irá se tornar:

Passo 4
Executando o código iremos obter o seguinte gráfico:
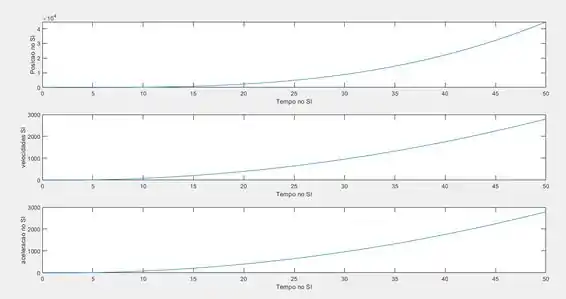
Resposta

Exercício Resolvido #3
“Elaboração Própria”
O programa abaixo representa o movimento oscilatório de uma partícula com e sem os efeitos dissipativos do arrasto devido a existência de um fluido qualquer.
Em uma mesma imagem, plote os gráficos do oscilador amortecido e não amortecido verticalmente alinhados. Cada gráfico deve conter título, descrição para os eixos coordenados:
Código:

Passo 1
A questão apresenta a parte inicial do código fonte e pede para que você plote as curvas de um oscilador amortecido e não amortecido em uma única janela gráfica.
Primeiramente iremos criar o algoritmo:
1-Entrada de dados
2-Criação e cálculo das funções
3-Finalização com o subplot.
Porém a questão já nos dá a primeira e segunda parte do algoritmo, então precisamos apenas inserir o terceiro passo, entende?
Passo 2
Uma vez que criamos o algoritmo iremos agora implementar o código no Matlab que já foi dado no Matlab:
Primeiramente, temos que implementar a entrada de dados:
Agora vamos criar o vetor tempo:
E agora iremos implementar as funções:
lembrando que quando iremos multiplicar os vetores, elemento a elemento precisamos colocar um ponto antes do operador, ok?
E vamos finalizar o código inserindo os subplots, como temos dois gráficos pois são duas funções iremos utilizar um subplot de coluna com duas linhas, então:
E nosso segundo gráfico se torna:
Implementando tudo corretamente iremos gerar a seguinte rotina:

Passo 3
Executando o código iremos obter o seguinte gráfico:
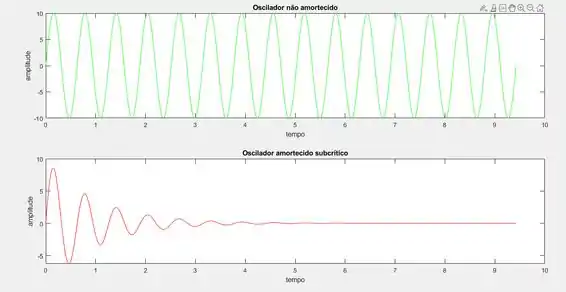
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
“Elaboração Própria”
Uma partícula é lançada obliquamente no vácuo, a em relação ao eixo X, suposto fixo no solo, e com uma elevação de. Construa uma representação gráfica revelando a trajetória dessa partícula, ao longo dos três eixos.
Para esse lançamento oblíquo em coordenadas esféricas utilize as seguintes equações:
Velocidades iniciais:
Deslocamento:
Passo 1
A questão pede para elaborarmos um programa em Matlab que a partir de dados iniciais possamos prever toda a dinâmica de uma partícula no vácuo em um espaço tridimensional.
A ideia aqui é realizar o subplot e plotar as curvas nos X,Y e Z e finalizar com uma curva 3d de linhas, ok?
Primeiramente iremos criar o algoritmo:
1-Entrada de dados
2-Criação e cálculo das funções
3-Finalização com a saída gráfica.
Uma vez que o algoritmo esteja pronto, vamos para o próximo passo.
Passo 2
Uma vez que criamos o algoritmo iremos agora implementar o código no Matlab.
Primeiramente, temos que implementar a entrada de dados:
Agora vamos criar o vetor tempo:
E agora iremos implementar as funções:
Passo 3
E vamos finalizar o código inserindo os subplots. Como temos 4 gráficos (três variáveis espaciais + a superfície 3D) para plotar, vamos criar um subplot para plotar as três variáveis espaciais e depois utilizaremos um comando figure para plotar a curva 3D.
O comando subplot divide a janela gráfica em uma matriz de gráficos, pra casos como essa questão, que nós temos vários gráficos. A sintaxe do subplot funciona da seguinte forma: são 3 argumentos: o primeiro diz quantas linhas essa matriz gráfica vai ter; o segundo argumento é o número de colunas; e o terceiro indica a ordem dos gráficos no subplot.
Como temos 3 gráficos (), vamos fazer uma matriz com 3 linhas e 1 coluna. E o gráfico em vai ser o primeiro, então o argumento do subplot fica .
E nosso segundo gráfico se torna:
O terceiro gráfico irá se tornar:
E por último iremos plotar a superfície 3D. Daí como os gráficos acima foram plotados numa figura só, o gráfico em 3D vai ser a segunda figura.
Implementando tudo corretamente iremos gerar a seguinte rotina:
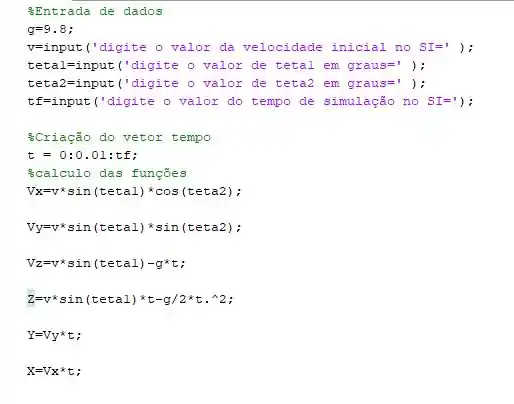

Passo 4
Executando o código iremos obter os seguintes gráficos:
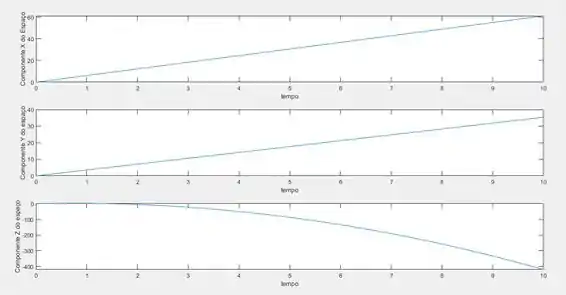
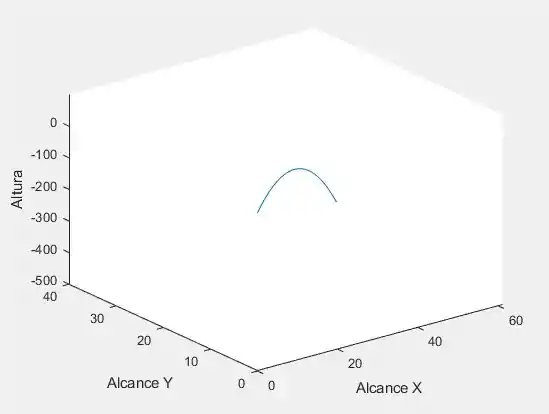
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Questão adaptada de “MATLAB com aplicações em engenharia – Exemplo Resolvido – Pagina 145”
O mecanismo constituído de uma manivela de êmbolo é usado em muitas aplicações na engenharia. No mecanismo mostrado a seguir, a manivela gira em uma velocidade constante de 50 rads/s.

Calcule e esboce a posição, a velocidade e a aceleração do êmbolo para uma revolução da manivela. Construa três gráficos na mesma janela de saída com todas as unidades no SI.
Utilize as seguintes equações para os cálculos:
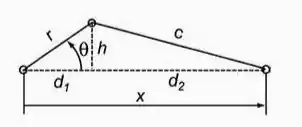
Posições:
Velocidades:
Aceleração:
Passo 1
A questão pede para elaborarmos um programa em Matlab que a partir de dados iniciais possamos prever toda a dinâmica do mecanismo apresentado na questão.
A ideia aqui é criar um vetor de tempo e calcular as variáveis cinemáticas do mecanismo e criar um subplot para plotar todas em uma única janela gráfica.
Primeiramente iremos criar o algoritmo:
1-Entrada de dados
2-Criação e cálculo das funções
3-Finalização com a saída gráfica.
Uma vez que o algoritmo esteja pronto, vamos para o próximo passo.
Passo 2
Uma vez que criamos o algoritmo iremos agora implementar o código no Matlab.
Primeiramente, temos que implementar a entrada de dados:
Agora vamos criar o vetor tempo:
E agora iremos implementar as funções:
E vamos finalizar o código inserindo os subplots, como temos 3 gráficos logo iremos gerar uma janela gráfica com 3 linhas e uma coluna, sendo assim o primeiro gráfico se torna:
E nosso segundo gráfico se torna:
O terceiro gráfico irá se tornar:
Implementando tudo corretamente iremos gerar a seguinte rotina:

Passo 3
Executando o código iremos obter os seguintes gráficos:
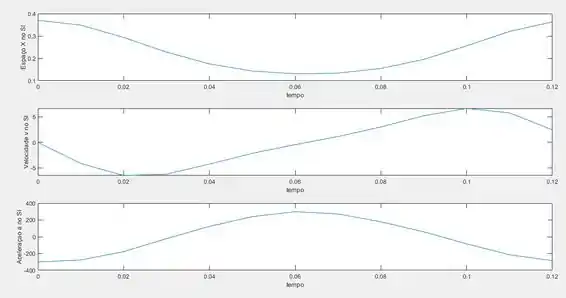
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Adaptada da Questão 10 - Matlab com aplicações em Engenharia – Amos Gilat – página 273
O deslocamento de uma borda é o nome dado a um defeito em uma amostra de cristal onde um grupo de átomos do cristal se desprende da estrutura cristalina. As componentes de tensão em volta da porção deslocada são dadas por:
Onde é o modulo de cisalhamento, é o módulo do vetor de Burgers e é a razão de Poisson. Plote as componentes de tensão devido ao deslocamento da borda de alumínio onde as tensões serão plotadas entre o intervalo:
Sendo:
Passo 1
Aqui é uma questão de plotagem onde iremos utilizar a função para uma melhor visualização das figuras.
A visualização se torna melhor pois conseguimos incluir as duas informações gráficas em uma mesma janela, tornando possível a realização de comparações para análises mais aprofundadas dos gráficos.
Então para a criação do precisamos criar o vetor para calcular as funções dentro desse intervalo desejado e depois disso imprimir o gráfico em uma janela gráfica utilizando a janela
Para criar o precisamos lembrar de sua sintaxe, primeiramente precisamos lembrar que o tem 3 argumentos na sua função.
O primeiro argumento da função vai falar quantas colunas o vai ter, aqui temos apenas dois gráficos logo duas colunas é suficiente.
Como temos 2 gráficos e colocamos duas colunas no nosso subplot o número de linhas se torna 1, que é o nosso segundo argumento. Sendo assim o subplot fica:
O terceiro índice é a numeração do gráfico que será explorado no final do exercício.
Sendo assim, o algoritmo se torna:
1-Criação do vetor e implementação dos dados do problema
2-cálculo das funções do problema
3-Implementação dos gráficos com o subplot e organização do mesmo.
Passo 2
Agora que montamos o nosso algoritmo vamos transformá-lo em um código do Matlab.
Primeiramente vamos criar o vetor arbitrariamente vou colocar um incremento de .
Agora vamos implementar os demais dados do problema.
Agora precisamos implementar as funções do problema:
Agora que criamos as funções vamos implementar os subplots.
Vou escolher arbitrariamente que o primeiro gráfico seja o do sigma, então o terceiro argumento do subplot fica 1 e vou indicar que nele irá localizar o plot da função sigma.
e agora iremos chamar a função onde iremos indicar no primeiro argumento o eixo e no segundo argumento a variável dependente.
Organizando os gráficos nomeando os eixos com a função , temos:
Analogamente vamos imprimir na segunda janela do subplot a função , então seu subplot fica:
Digitando tudo certinho seu código fica:

Executando o código temos o seguinte gráfico.
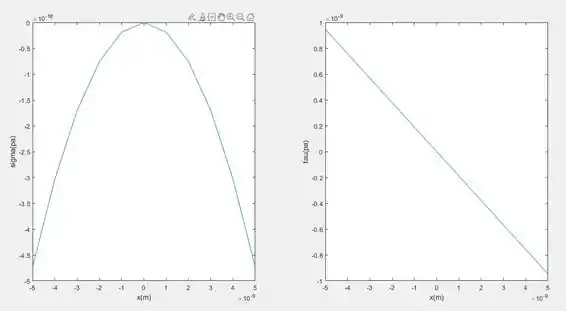
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Questão 4 – página 291- Matlab com Aplicações a engenharia – Amos Gilat
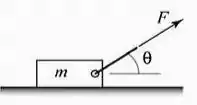
Um bloco de massa está sendo puxado por uma corda. O módulo da força necessária para movimentar o bloco é dado por:
Onde e é chamado de coeficiente de atrito e e é chamada de aceleração da gravidade.
Determine o ângulo e a massa máxima no qual a força seja equivalente a
Passo 1
Aqui temos uma questão de subplot, a questão em si pode ser resolvida de diversas formas, porém o subplot se torna uma alternativa mais simples.
O subplot se torna uma alternativa simples pois estamos procurando um conjunto de valores de ângulo e massa pelo o qual a força exercida para movimentar o bloco seja equivalente a .
Como o subplot conseguimos colocar diversos gráficos em uma mesma janela, analisar o gráfico para obter essa informação fica muito mais simples.
Para resolução do problema precisamos criar dois vetores para fazer a função dada no problema variar e encontrarmos esses valores.
O primeiro vetor é o vetor de ângulo que vamos variar de 0 até .
Porque quando passamos de pelo desenho vamos puxar o bloquinho na direção contrária.
E a massa vai variar de 0 até 20 kg, pois um bloco de mais de 21 kg não parece fisicamente muito normal de se encontrar sendo puxado por uma cordinha, belezinha?
Para finalizar vamos calcular a função sob esses vetores e vamos finalizar imprimindo um graficozinho para melhor analisar e obter a nossa resposta.
Sendo assim, o algoritmo para a resolução do problema se torna:
1-Implementação da entrada de dados.
2-Criação dos vetores Massa e Ângulo.
3-Cálculo da força.
4-plotagem utilizando o subplot.
Passo 2
Agora que criamos o algoritmo vamos implementá-los no Matlab.
Primeiramente vamos implementar a entrada de dados dentro do Matlab.
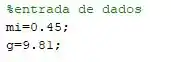
Agora que já implementamos a entrada de dados, o segundo passo é implementar os vetores de massa e ângulo.
O vetor de massa vamos implementar com uma variação de 1, para não ficar muito ponto e o cálculo não ficar pesado, arbitrariamente vamos chamar essa variável de M.
![]()
Agora vamos implementar os valores de teta, com o teta variando de 0 até , gostaríamos que tivesse a mesma quantidade de pontos que a variável M.
Para isso definimos o incremento como sendo:
Fazendo com que o vetor teta tenha 20 elementos e resultando em:
![]()
Agora que implementamos os valores dos ângulos vamos calcular a função desejada:
![]()
Lembrando que estamos realizando uma operação elemento a elemento do vetor, como nós temos um vetor M sendo dividido pelo vetor temos que colocar o ponto “.” Para indicar a operação elemento a elemento.
Passo 3
Agora vamos iniciar o plot, para isso vamos primeiramente falar do subplot.
Para criar o precisamos lembrar de sua sintaxe, primeiramente precisamos lembrar que o tem 3 argumentos na sua função.
O primeiro argumento da função vai falar quantas colunas o vai ter, aqui temos apenas dois gráficos logo duas colunas é suficiente.
Como temos 2 gráficos e colocamos duas colunas no nosso subplot o número de linhas se torna 1, que é o nosso segundo argumento. Sendo assim o subplot fica:
Vou escolher arbitrariamente que o primeiro gráfico seja o do teta então o terceiro argumento do subplot fica 1 e vou indicar que nele irá localizar o plot da função .
e agora iremos chamar a função onde iremos indicar no primeiro argumento o eixo e no segundo argumento a variável dependente.
![]()
Agora vamos nomear os eixos para ficar algo mais organizado e para isso iremos precisar de duas funções. A função e a outra se chama a .
Para nomear os eixos precisa apenas fazer o seguinte procedimento:
Ou seja, precisamos apenas chamar a função, colocar o igual e escrever entre aspas simples o nome do eixo.
Na realidade estamos anexando um string aos eixos.
Analogamente vamos imprimir na segunda janela do subplot, então seu subplot fica:

Digitando tudo certinho seu código fica:

Passo 4
Executando o código irá obter os seguintes gráficos.

E analisando as curvas acima podemos verificar que os valores para obter uma força de 100 N são aproximadamente teta=1,3 raianos e um valor de Massa igual a 17 kg.
Passo 5
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
Questão 9 – página 292- Matlab com Aplicações à engenharia – Amos Gilat
A lei de radiação de corpo negro de Planck dá a radiância espectral em função do comprimento de onda e da temperatura T (em kelvin)
Onde é a velocidade da luz, é a constante de Planck e é a constante de Boltzman.
Plote R em função de para valores de m e com a temperatura com valores de .
Em seguida, determine o comprimento de onda e a temperatura que resulta a máxima radiância espectral possível.
Passo 1
Aqui temos uma questão de subplot, a questão em si pode ser resolvida de diversas formas, porém o subplot se torna uma alternativa mais simples.
O subplot se torna uma alternativa simples nesse caso pois estamos procurando um conjunto de entradas que façam com que nossa função radiância detenham o maior valor possível dentro daquele intervalo.
Como o subplot conseguimos colocar diversos gráficos em uma mesma janela, analisar o gráfico para obter essa informação fica muito mais simples.
Para resolução do problema precisamos criar dois vetores para fazer a função dada no problema variar e encontrarmos esses valores.
O primeiro vetor é o vetor de temperaturas que vamos impor um incremento de:
Para não gerar pontos demais e deixar o cálculo lento.
E para termos o mesmo número de pontos dentro de ambos os vetores vamos impor um incremento de:
Para finalizar vamos calcular a função sob esses vetores e vamos finalizar imprimindo um graficozinho para melhor analisar e obter a nossa resposta.
Sendo assim, o algoritmo para a resolução do problema se torna:
1-Implementação da entrada de dados.
2-Criação dos vetores Temperatura e comprimento de onda.
3-Cálculo da função.
4-plotagem utilizando o subplot.
Passo 2
Agora que criamos o algoritmo vamos implementá-los no Matlab.
Primeiramente vamos implementar a entrada de dados dentro do Matlab.
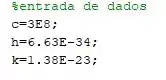
Agora que já implementamos a entrada de dados, o segundo passo é implementar os vetores de temperatura e comprimento de onda, que vamos chamar arbitrariamente de T e lambda respectivamente.
Para deixarmos ambos os vetores com 20 elementos prec

Agora que implementamos os valores dos ângulos vamos calcular a função desejada:

Lembrando que estamos realizando uma operação elemento a elemento do vetor, como nós temos um vetor então precisamos colocar um ponto “.” Para indicar essa operação.
Por exemplo no início temos , aqui temos que lembrar de colocar o ponto para elevar o vetor lambda a potência mas também temos que colocar para realizar a divisão belezinha?
Passo 3
Agora vamos iniciar o plot, para isso vamos primeiramente falar do subplot.
Para criar o precisamos lembrar de sua sintaxe, primeiramente precisamos lembrar que o tem 3 argumentos na sua função.
O primeiro argumento da função vai falar quantas colunas o vai ter, aqui temos apenas dois gráficos logo duas colunas é suficiente.
Como temos 2 gráficos e colocamos duas colunas no nosso subplot o número de linhas se torna 1, que é o nosso segundo argumento. Sendo assim o subplot fica:
Vou escolher arbitrariamente que o primeiro gráfico seja o do teta então o terceiro argumento do subplot fica 1 e vou indicar que nele irá localizar o plot da função .
e agora iremos chamar a função onde iremos indicar no primeiro argumento o eixo e no segundo argumento a variável dependente.
![]()
Agora vamos nomear os eixos para ficar algo mais organizado e para isso iremos precisar de duas funções. A função e a outra se chama a .
Para nomear os eixos precisa apenas fazer o seguinte procedimento:
Ou seja, precisamos apenas chamar a função, colocar o igual e escrever entre aspas simples o nome do eixo.
Na realidade estamos anexando um string aos eixos.
Analogamente vamos imprimir na segunda janela do subplot, então seu subplot fica:

Digitando tudo certinho seu código fica:
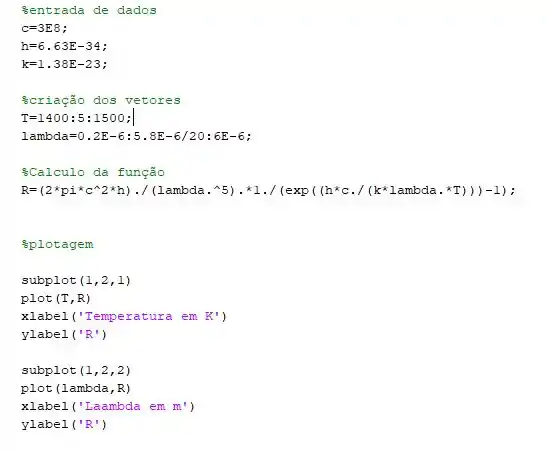
Passo 4
Executando o código irá obter os seguintes gráficos.
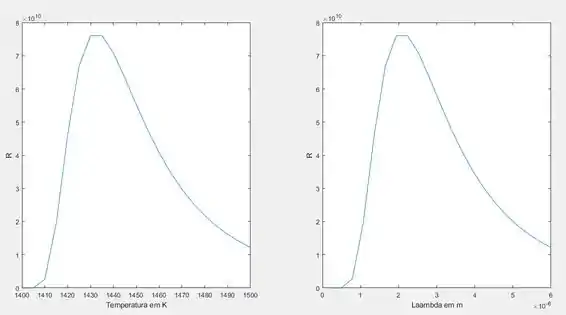
E analisando a curva podemos perceber que a função obtém seu valor máximo para uma temperatura em torno de 1430 Kelvin com um comprimento de onda de .
Passo 5
Resposta
Ei, a resposta está no passo a passo :)