Operações com Polinômios (Zeros, Soma, Produto e Divisão de Polinômios)
Produzido por Gustavo BarbosaTeoria
Iae como você está?
Está tudo bem?
Espero que sim, pois hoje iremos bater mais um papinho sobre polinômios. Imagine que você está em uma aula de cálculo e você precisa encontrar os zeros do seguinte polinômio:
Ou mesmo escrever uma rotina para a resolução de uma equação do tipo:
É complicadinho demais né?
E se eu te falar que existe uma função no Matlab que faz isso em apenas 2 linhas de código, você acreditaria?

E não só existe essa ferramenta, na realidade existe uma infinidade de ferramentas para se trabalhar polinômios dentro do matlab e hoje iremos ver as mais importantes, tranquilo?
Entãaaaaaaao vai pegar o papel e a caneta porque iremos começar.
Encontrando os zeros de polinômios
O zero de um polinômio é o valor da variável independente para o qual o polinômio se anula.
Para encontrar os zeros de uma função polinomial no Matlab nós utilizamos a função e para ficar mais claro vamos explicar essa função através de um exemplo.
Primeiramente vamos inserir o seguinte polinômio no Matlab:
O vetor dos coeficientes do polinômio é dado por:
E pra encontrar a raiz do polinômio vamos chamar a função , cuja sintaxe é dada por:
No Matlab o mini código deve ficar algo mais ou menos assim:
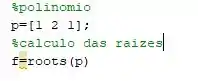
E executando o código, você irá obter a seguinte resposta:
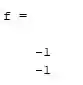
Ou seja, as duas raízes do polinômio de grau dois são dadas por:
Mas aí vem a pergunta, se eu já tiver os valores das raízes o Matlab consegue encontrar o polinômio?
E MEU AMIGO, ELE CONSEGUE SIIIIIIIIIIIIM HAHAHHAHA

E para isso iremos utilizar uma outra função chamada de , e sua sintaxe também é simples.
Primeiramente precisamos criar o vetor com as raízes do polinômio, vamos utilizar o exemplo anterior cuja as raízes são iguais a
No Matlab isso fica assim:
E agora chamamos a função poly:
Seu mini código ficará algo assim:
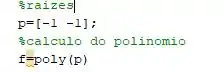
Executando o código, teremos o seguinte resultado:

Ou seja, retornaremos aos coeficientes que geram o seguinte polinômio:
Adição de polinômios
Como estamos trabalhando com vetores, a adição de polinômios é realizada da mesma forma como se estivéssemos somando vetores.
Por exemplo, se eu tenho os seguintes polinômios:
E eu quero somar ambos os polinômios, sabemos das aulas de álgebra que só podemos somar os termos que estão na mesma base, ou seja so irá se somar com , e daí por diante.
Então para somar precisamos realizar a seguinte operação:
Vamos inserir primeiro o vetor de maior potência, lembrando que os termos que não aparecem no polinômio são representados por um zero multiplicando a potência de , ou seja, nesse polinômio o esta da seguinte forma: . Ok?
Então o polinômio fica:
Já o segundo polinômio precisa ter o mesmo número de coeficientes escritos e, como não temos termos acima de , colocamos todos como zero:
E finalmente a soma dos polinômios é dada por:
Colocando isso no command Windows temos os seguintes resultados:
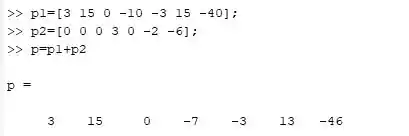
E o mesmo é feito pra subtração de polinômios, só substituindo o por !
Multiplicação de polinômios
Na matemática dois polinômios se multiplicam utilizando a relação de distributividade da álgebra, logo para realizar a multiplicação de dois polinômios, o Matlab usa uma função especial chamada de função .
Vamos utilizar os vetores do exemplo anterior:
E agora vamos realizar o produto entre os polinômios utilizando a função
Utilizando o command windows o resultado que irá aparecer é o seguinte:
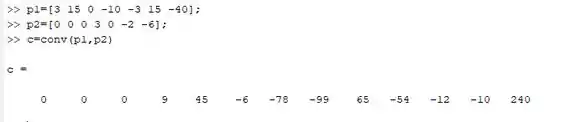
Agora vem a pergunta: se tivéssemos produtos de mais de dois polinômios? Por exemplo, temos além de e , tivéssemos o polinômio:
Para resolver um problema de mais de dois polinômios precisamos resolver por partes, ou seja, fizemos a multiplicação de e e anexamos a informação na variável
Agora vamos multiplicar o polinômio que está na variável pelo , logo no matlab deve ficar algo assim:
E deve mostrar o seguinte resultado:
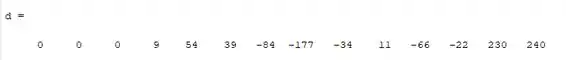
Divisão de polinômios
Finalmente chegamos na última operação né?
Essa aqui é a operação de divisão, lembra como realiza a divisão entre dois polinômios?
No ensino médio utilizamos a seguinte regrinha, sejam e dois polinômios, onde o grau de deve ser maior do que o grau de , temos que:
Onde é um polinômio qualquer e o é o resto da divisão, então quando efetuamos uma divisão de dois polinômios temos duas saídas: a primeira é o polinômio e a segunda é o polinômio .
Você deve estar se perguntando “E de que isso me importa?”, bem é que quando realizamos uma divisão no Matlab ele nos dá dois resultados.
Esses dois resultados são os polinômios q e o resto.
Para entender melhor vamos resolver a seguinte divisão:
Para realizar essa divisão vamos inserir os dois polinômios no Matlab, tanto o numerador quanto o denominador.
Então primeiramente vamos inserir os polinômios:
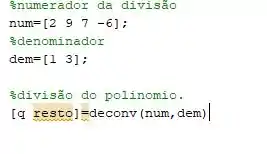
Agora vamos realizar a divisão, para isso vamos utilizar a função , e lembra que falamos que uma divisão gera duas saídas?
Para não gerar erros, vamos padronizar as variáveis da seguinte forma:
As nomeações das variáveis podem ser de forma arbitrária, mas a ordem é sempre assim, ok?
Inserindo no Matlab temos o seguinte código:
Executando o código iremos obter o seguinte resultado:

Ou seja, o resultado é dado por:
Opa galeraaa chegamos ao fimmm, hoje ficaremos por aqui e não esqueçam de dar uma olhadinha nos exercícios, okay? Escolhemos todos com bastante carinho para você praticar!