Curvas Tridimensionais
Produzido por Gustavo BarbosaTeoria
Alguns aspectos introdutórios.
Iae ta tudo bem? Como você está?
Hoje iremos conversar mais um pouco sobre saídas de dados na forma gráfica
No Matlab, podemos usar vários tipos de gráficos de acordo com o conjunto de dados que estamos trabalhando.
O mais comum é representar os dados na forma de curvas bidimensionais, mas nem sempre essa é a melhor forma, por isso, hoje vamos conhecer uma alternativa: as curvas tridimensionais.
Mas para que servem as curvas tridimensionais né?

Vamos ver num exemplo! Imagine que você trabalha para uma certa empresa, e a empresa lhe apresenta que o preço de mercado é descrito pela seguinte função:
Onde corresponde ao preço de mercado, a oferta e a demanda respectivamente.
Mesmo sendo uma ótima alternativa, a representação por funções gera uma certa confusão uma vez que se trata de uma análise pontual.
Imagine se seu chefe lhe perguntar a tendência do preço de mercado entre as variações das demandas e ofertas simultaneamente, só olhando os valores da função fica mais complicado de responder né?
Mas, se você tivesse esse gráfico abaixo?
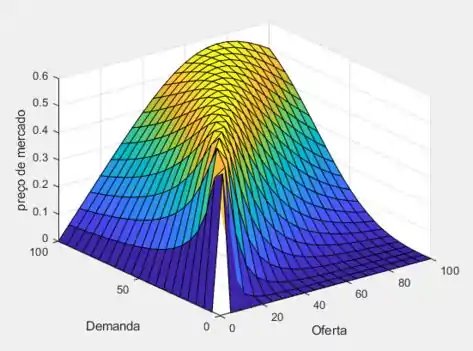
A tarefa se tornaria mais simples, né? O que você acha?
Então as superfícies tridimensionais são na realidade uma outra forma de apresentar os resultados, que a depender da situação pode-se melhor ajustar a seu problema.
Mas aí vem a pergunta “como criar isso? ”
Calma, calma que vamos aprender isso já já.
Comando meshgrid
Na prática a variável que chamamos de preço de mercado, estamos associando a outras duas variáveis chamadas de oferta e demanda.
Mas essa associação não é feita de qualquer forma, nós criamos um plano de duas dimensões que chamamos de malha e associamos cada variável que chamamos de preço de mercado a um par coordenado de pontos de oferta e demanda, similar ao plano cartesiano que observamos no segundo grau.
Mas como criar essa malha? A resposta é a função !
A sintaxe dessa função é:
- os colchetes indicam que a saída do meshgrid é uma matriz de pares coordenados.
- a entrada da função é alimentada pelas variáveis e .
Obs: essas variáveis receberam esses nomes de forma arbitrária, você pode inserir qualquer nome para elas.
Comando surf
Uma vez que criamos a malha com o comando , precisamos apenas criar a superfície utilizando a função .
Para aprender a utilizar esses comandos vamos fazer um exemplo simples, vamos plotar a superfície da função:
Cujo o domínio da função está entre os intervalos:
Primeiramente iremos criar os vetores e para o cálculo dos valores de , para isso iremos colocar no Matlab a seguinte informação:
Usamos um incremento bem pequeno entre os pontos de e pra deixar o gráfico que vamos gerar mais contínuo.
Agora que inserimos os eixos vamos criar a malha:
Uma vez que a malha está criada vamos representar a função no Matlab:
Como e são vetores, precisamos colocar um ponto após eles na fórmula para que as contas sejam feitas elemento a elemento.
Agora vamos criar a superfície tridimensional:
Aqui, listamos os três conjuntos de dados que formam nosso gráfico. O primeiro fica no eixo , o segundo no e o terceiro no .
Agora que já criamos a superfície vamos nomear os eixos utilizando os seguintes comandos:
Para ‘embelezar’ a curva podemos ainda adicionar o comando de escala, que em geral é um comando muito útil pois ele deixa bem mais visual os dados existentes dentro da nossa superfície e ainda adiciona valores numéricos para uma melhor visualização e entendimento da superfície de uma forma gráfica e facilmente entender seus maiores e menores valores.
Mas a sua utilização é opcional, belezinha?
Executando o código abaixo, o Matlab irá mostrar a seguinte superfície:
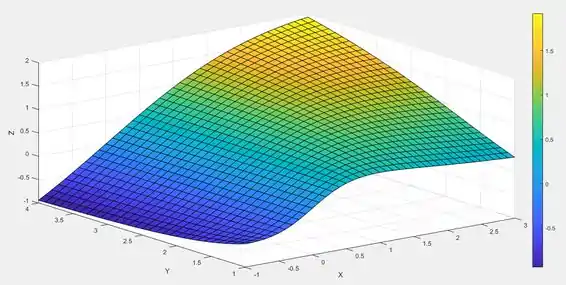
Existem diversas outras formas de superfícies tridimensionais, a estrutura geral é dada de forma similar a curva anterior, por exemplo, se você quiser uma curva de linhas basta trocar o por.
E seu código irá gerar a seguinte curva:
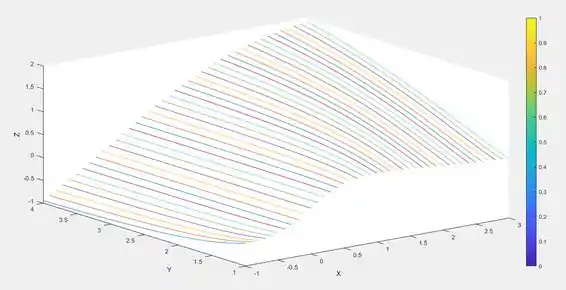
Ou se deseja as curvas de nível da superfície tridimensional, basta trocar a função por e a superfície plotada será:

Existe uma infinidade de superfícies que podem ser encontradas no site do Matlab, mas em geral para cursos de engenharia utilizamos essas três representações e por isso que essas foram escolhidas.
Bem pessoal, hoje ficaremos por aqui, mas não deixe de praticar, escolhemos uma série de exercícios bem interessantes para vocês. AAAAAAAAAAH e antes que eu me esqueça dê uma olhadinha no site do Matlab e veja os comandos das demais superfícies.
Nunca se sabe quando podem ser úteis né?