Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Derivadas Numéricas

Ver Todos os Exercícios

Teoria

Introdução

Olá, meu povo! Lembram das derivadas de Cálculo I? Usamos elas pra estudar variações de uma função ao longo de uma variável.

Por exemplo, se temos uma função que calcula a posição de um carro ao longo do tempo, sua primeira derivada indica a velocidade do carro e a segunda, a aceleração.

Quando se conhece a função que queremos derivar e é fácil de encontrar sua derivada (por exemplo, uma função polinomial tipo f ( x )   =   x 2 ou uma função que a gente encontra naquelas tabelas de derivadas) podemos resolver isso na mão em dois palitos.

Mas imagina que você fez um experimento medindo a velocidade em rpm de um motor elétrico, inicialmente parado, aplicando uma tensão constante nele. Você registrou em uma tabelinha a velocidade do motor a cada instante de tempo.

Você quer encontrar a taxa de variação de velocidade do motor, isto é, a aceleração. Como fazer isso sem conhecer a função matemática que descreve a velocidade do motor em função do tempo?

Nosso amigo MATLAB pode ajudar a gente a resolver isso! Para casos em que queremos encontrar as derivadas tendo apenas tabelas com valores, usamos a diferenciação numérica.

A função d i f f ( ) do MATLAB ajuda a gente a calcular a diferenciação numérica com vetores de valores. Partiu aprender mais essa funçãozinha do MATLAB?

Entendendo a função d i f f ( )

Podemos ter duas entradas na função d i f f ( ) e ela nos retorna uma saída:

Y   =   d i f f ( X ,   n )

Ela calcula n   vezes a diferença entre os elementos adjacentes do vetor X e nos dá o resultado na forma do vetor Y .

Vamos traduzir isso com um exemplo. Se nosso vetor X é [ 1   2   3   4   5 ] e usamos n   =   1 , entramos as seguintes linhas de código no Command Window do MATLAB:

Ele vai nos retornar:

Para construir o vetor Y , o MATLAB fez:

Y = [ 2 - 1   3 - 2   4 - 3   5 - 4     ] = [ 1   1   1   1     ]

Isto é, ele fez um elemento menos o elemento à sua esquerda, começando com o segundo elemento de X , e a diferença foi calculada só uma vez. Caso eu fizesse Y   =   d i f f ( X , 2 ) , o resultado seria:

Neste caso, a diferença foi feita duas vezes, pois n   =   2 . Primeiro o MATLAB fez:

[ 2 - 1   3 - 2   4 - 3   5 - 4     ] = [ 1   1   1   1     ]

Em seguida:

1 - 1   1 - 1   1 - 1   = 0   0   0  

Na prática, seria a mesma coisa que fazer Y   =   d i f f ( d i f f ( X , 1 ) , 1 ) , sacou?

Note que o vetor de saída Y sempre terá um elemento a menos do que o vetor de entrada X , por causa deste esquema de fazer um elemento menos o elemento à sua esquerda.

Na função Y   =   d i f f ( X , n ) , a entrada n é opcional. Se usarmos simplesmente Y   =   d i f f ( X ) , o MATLAB calcula a diferença uma vez só. Em outras palavras, o padrão é n   =   1 .

Diferenciação Numérica no MATLAB

Ok, já sabemos como funciona o d i f f ( ) , mas como usamos ele para calcular derivadas numéricas? Vamos aprender tendo como exemplo o experimento do motor. Imagine se tivéssemos uma expressão algébrica que representasse a velocidade do motor em função do tempo. Ela teria essa cara:

v   =   f ( t )

onde v é a velocidade do motor e t é o tempo. Para encontrar a variação da velocidade do motor ao longo tempo, eu teria que derivar essa função no tempo:

d v d t = d f ( t ) d t

Falando de um jeito beeem simplificado, na diferenciação numérica do nosso exemplo, temos que encontrar dois vetores, um representando d v e outro representando d t . O vetor d v teria a diferença de velocidades de um instante de tempo para outro e o vetor d t teria a diferença entre um instante de tempo e outro. Daí, para encontrarmos d v / d t , temos que dividir cada elemento de d v por um elemento de d t que esteja na mesma posição.

Vamos ilustrar isso no MATLAB. Primeiro, vamos criar dois vetores, um para o tempo e outro para a velocidade do motor:

O vetor do tempo eu chamei de t e, como o tempo foi registrado de um em um segundo, eu posso criá-lo usando os dois pontos, pedindo que ele comece em 0 e vá até 9 , de um em um.

O vetor de velocidade chamei de v . Dividi os valores de v por 60 para converter rpm (rotações por minuto) para rps (rotações por segundo), para que a unidade de velocidade seja compatível com a unidade de tempo do vetor t .

Agora, vamos usar a função d i f f ( ) para calcular os vetores d v e d t :

Para encontrarmos a derivada d v / d t , entramos com a linha de código:

Chamei a derivada d v / d t de d v d t e a calculei dividindo cada elemento de d v pelo elemento de d t que está na mesma posição. Então, d v d t também é um vetor e tem essa carinha:

Interpretando o resultado, temos que a aceleração do motor entre os instantes 0 e 1 s do experimento é de 20,1667 rps²; entre os instantes 1 e 2 s, ela é de 10,9333 rps², e assim sucessivamente.

Mais uma aplicaçãozinha

Para fechar, vamos ver mais um exemplo. Desta vez, não temos uma tabela com valores, nós conhecemos a expressão algébrica da função que queremos derivar. Digamos que eu queira calcular a derivada numérica do polinômio abaixo no intervalo [ - 4 ; 5 ] :

f x = x 5 - 3 x 4 - 11 x 3 + 27 x 2 + 10 x - 24

Chamando d f / d x de d f d x , eu crio um script no MATLAB com as seguintes linhas de código:

Vamos ver o que cada linha significa:

  • Na linha 1, crio o vetor x , que vai de - 4 a 5 , a um passo de 0,1 .
  • Na linha 2, eu entro com o polinômio, que vai ser representado pelo vetor f . Cada elemento de f é a solução de f ( x ) para cada elemento do vetor x . Eu faço isso usando o . do lado de x . Por exemplo, x . ^ 5 significa que cada elemento do vetor x é elevado à quinta potência.
  • Na linha 3, eu calculo a derivada do polinômio, usando o d i f f ( ) .
  • Na linha 5, crio um vetor x d que vai do 2º elemento de x até o último elemento dele (por isso o e n d no final). Lembra que o vetor de saída do d i f f ( ) tem um elemento a menos do que o vetor de entrada? Se tentarmos criar o plot com vetores de tamanhos diferentes, o Matlab dá erro, por isso criamos esse vetor pra fazer o plot da derivada;
  • Na linha 7, eu peço ao MATLAB para gerar o gráfico do meu polinômio, tendo o vetor x no eixo x do gráfico e o vetor f no eixo y ;
  • Na linha 8, eu uso o comando h o l d   o n . Com esse comando, eu faço com que meu plot seguinte não substitua o plot da linha 7. Desta forma, eu posso ter as duas curvas, a da função e a da derivada, na mesma janela;
  • Finalmente, na linha 9, eu peço ao MATLAB para gerar o gráfico da derivada do polinômio, tendo o vetor x d no eixo x e o vetor d f d x no eixo y .

Rodando o nosso código, temos este gráfico maravilhoso no final:

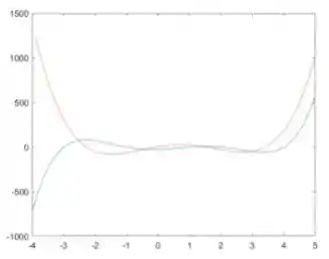
Em azul, temos o polinômio f x = x 5 - 3 x 4 - 11 x 3 + 27 x 2 + 10 x - 24 .

Em vermelho, temos a primeira derivada de f x .

E aí, curtiu? Sentindo que agora encara qualquer derivada? Para ganhar mais confiança, bora praticar com os exercícios que eu preparei com muito carinho para te ajudar a fixar o conteúdo ;D

Entendendo a função d i f f ( )

Diferenciação Numérica no MATLAB

Mais uma aplicaçãozinha

Exercícios Resolvidos

Exercício Resolvido #1

Adaptado de UERJ, “Curso de MATLAB 5.1: Introdução à Solução de Problemas de Engenharia”, Laboratório de Engenharia Elétrica, p. 128

Para o polinômio abaixo, plote a função e sua derivada, no intervalo de [-10,10], usando diferenciação numérica.

h x = x 5 - 4 x 4 - 9 x 3 + 32 x 2 + 28 x - 48

Passo 1

A questão nos pede para gerarmos um gráfico com duas curvas, uma representando h ( x ) e outra representando d h d x , com x indo de -10 a 10.

Antes de gerarmos as curvas com função p l o t ( ) , precisamos encontrar a derivada de h ( x ) , usando diferenciação numérica. Para isso, usaremos a função d i f f ( ) do MATLAB.

Passo 2

Primeiramente, crie um script novo no MATLAB e digite o código abaixo, para gerar um vetor contendo o intervalo de x pedido no enunciado:

O comando acima cria um vetor chamado x cujos elementos vão de -10 a 10, com um passo de 0,01. Escolhi um passo pequeno para as curvas no final saírem suaves, mas você pode escolher o passo que quiser.

Em seguida, precisamos calcular h ( x ) para cada elemento do vetor x . Para isso, digite a linha de código:

Nesta linha de código, colocamos um ponto (.) ao lado do vetor x indicando que queremos realizar a operação matemática em cada elemento dele. Por exemplo, x . ^ 5 pede que cada elemento de x seja elevado à quinta potência. Desta forma, criamos um vetor chamado h , de mesmo tamanho de x , que contém o resultado de h ( x ) para cada elemento do vetor x .

Passo 3

Para encontrarmos d h d x por diferenciação numérica, temos que gerar dois vetores, um representando d h e outro representando d x . O vetor d h teria a diferença de h ( x ) de um valor de x a outro e o vetor d x teria a diferença entre um valor de x e outro.

Estes vetores são gerados por meio da função d i f f ( ) . Lembrando que ela tem a seguinte estrutura:

Y   =   d i f f ( X ,   n )

Ela calcula n   vezes a diferença entre os elementos adjacentes do vetor X e nos dá o resultado na forma do vetor Y .

Os dois vetores são gerados por meio das seguintes linhas de código:

Na primeira linha, é criado o vetor d x , que contém as diferenças entre elementos adjacentes do vetor x . Para criar o vetor d x , a função d i f f ( ) faz um elemento de x menos o elemento à esquerda, começando a partir do segundo elemento de x .

Na segunda linha, é feita a mesma coisa, mas com o vetor h . A variação de h é armazenada no vetor d h .

Note que não entramos nenhum valor para n , porque queremos que a diferença seja feita uma vez. Quando não entramos com nenhum valor para n na função d i f f ( ) , por o padrão o MATLAB adota n = 1 .

Passo 4

Com os vetores d x e d h criados, podemos calcular d h d x por meio da linha de código:

Com este comando, dividimos cada elemento do vetor d h pelo elemento do vetor d x que esteja na mesma posição e o resultado é armazenado no vetor d h d x .

O vetor d h d x representa a derivada de h ( x ) obtida por meio de diferenciação numérica. Com o vetor d h d x , podemos gerar o gráfico de d h d x .

Passo 5

Antes de gerar o gráfico de h ( x ) e de d h d x , precisamos criar um vetor auxiliar para podermos plotar a curva de d h d x em função de x . Esse vetor auxiliar é necessário por que o vetor d h d x tem um elemento a menos do que x , o que levaria a um erro na função p l o t ( ) .

Vamos chamar o vetor auxiliar de x d e criá-lo da seguinte forma:

A linha de código acima diz que o vetor x d é um pedaço do vetor x , começando do segundo elemento de x e indo até o final de x (indicando por e n d ).

Já temos tudo o que precisamos para gerar os gráficos de h ( x ) e de d h d x . Vamos criar as curvas de ambos na mesma janela. Para isso, entre as três linhas de código abaixo:

Na primeira linha, pedimos ao MATLAB para plotar h em função de x e d h d x em função de x d .

Na segunda linha, damos um nome ao eixo x do gráfico: chamamos ele de x.

Na terceira linha, criamos uma legenda para o gráfico. A string ‘ h ( x ) ’ é a legenda da curva gerada pelo primeiro par de vetores, x e h , da função p l o t ( ) . Já a string ‘ d h / d x ’ é a legenda da curva gerada pelo segundo par de vetores, x d e d h d x , da função p l o t ( ) .

Rodando nosso programa, temos o gráfico pedido no enunciado:

A curva azul representa h ( x ) e a curva vermelha, d h d x .

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #2

Adaptado de UERJ, “Curso de MATLAB 5.1: Introdução à Solução de Problemas de Engenharia”, Laboratório de Engenharia Elétrica, p. 128

Para o polinômio abaixo, plote a função, sua derivada primeira e sua derivada segunda, no intervalo de [-10,10]. Use diferenciação numérica para encontrar as derivadas.

i x = x 7 - 5 x 3 + 14 x 2 - 12

Passo 1

A questão nos pede para gerarmos um gráfico com três curvas, uma representando i ( x ) , outra representando d i d x (a derivada primeira de i ( x ) ) e outra representando d 2 i d x 2 (a derivada segunda de i ( x ) )) com x indo de -10 a 10.

Antes de gerarmos as curvas com função p l o t ( ) , precisamos encontrar as derivadas de i ( x ) , usando diferenciação numérica. Para isso, usaremos a função d i f f ( ) do MATLAB. Lembrando que ela tem a estrutura:

Y   =   d i f f ( X ,   n )

Ela calcula n   vezes a diferença entre os elementos adjacentes do vetor X e nos dá o resultado na forma do vetor Y .

Para encontrarmos a derivada primeira, o vetor X   de entrada de d i f f ( ) será a função i ( x ) . Para a derivada segunda, o vetor X será d i d x .

Nos passos abaixo, vamos entender direitinho o porquê.

Passo 2

Primeiramente, crie um script novo no MATLAB e digite o código abaixo, para gerar um vetor contendo o intervalo de x pedido no enunciado:

O comando acima cria um vetor chamado x cujos elementos vão de -10 a 10, com um passo de 0,01. Escolhi um passo pequeno para as curvas no final saírem suaves, mas você pode escolher o passo que quiser.

Em seguida, precisamos calcular i ( x ) para cada elemento do vetor x . Para isso, digite a linha de código:

Nesta linha de código, colocamos um . ao lado do vetor x indicando que queremos realizar a a operação matemática em cada elemento dele. Por exemplo, x . ^ 7 pede que cada elemento de x seja elevado à sétima potência. Desta forma, criamos um vetor chamado i , de mesmo tamanho de x , que contém o resultado de i ( x ) para cada elemento do vetor x .

Passo 3

Depois de criarmos os vetores x e i , podemos determinar as derivadas primeira e segunda de i ( x ) . Vamos começar com a a derivada primeira. Para encontrarmos d i d x por diferenciação numérica, temos que gerar dois vetores, um representando d i e outro representando d x . O vetor d i teria a diferença de i ( x ) de um valor de x a outro e o vetor d x teria a diferença entre um valor de x e outro.

Estes vetores são gerados por meio da função d i f f ( ) , que tem a estrutura:

Y   =   d i f f ( X ,   n )

Ela calcula n   vezes a diferença entre os elementos adjacentes do vetor X e nos dá o resultado na forma do vetor Y .

Os dois vetores são gerados por meio das seguintes linhas de código:

Na primeira linha, é criado o vetor d x , que contém as diferenças entre elementos adjacentes do vetor x . Para criar o vetor d x , a funçao d i f f ( ) faz um elemento de x menos o elemento à esquerda, começando a partir do segundo elemento de x .

Na segunda linha, é feita a mesma coisa, mas com o vetor i . A variação de i é armazenada no vetor d i .

Note que não entramos nenhum valor para n , porque queremos que a diferença seja feita uma vez. Quando não entramos com nenhum valor para n na função d i f f ( ) , por o padrão o MATLAB adota n = 1 .

Passo 4

Com os vetores d x e d i criados, podemos calcular d i d x por meio da linha de código:

Com este comando, dividimos cada elemento do vetor d i pelo elemento do vetor d x que esteja na mesma posição e o resultado é armazenado no vetor d i d x .

O vetor d i d x representa a derivada primeira de i ( x ) obtida por meio de diferenciação numérica. Com o vetor d i d x , podemos gerar o gráfico de d i d x .

Passo 5

Após determinarmos a primeira derivada, vamos calcular a segunda derivada de i ( x ) , por meio de diferenciação numérica. Assim como fizemos para a primeira derivada no passo 3, para determinar d 2 i d x 2 , precisamos construir dois vetores, um representando d 2 i e outro representando d x 2 , e dividir um pelo outro.

Para isto, usamos a função d i f f ( ) de novo. No MATLAB, digite a linha de código:

Com este comando, aplicamos a função d i f f ( ) no vetor d i d x , que representa d i d x , e armazenamos o resultado no vetor d 2 i . Calculando a diferença entre os elementos adjacentes de d i d x , é como se estivéssemos calculando a derivada de d i d x , que é consequentemente d 2 i d x 2 .

d 2 i é o nosso vetor representando d 2 i . Para criar o vetor d x 2 , vamos criar um vetor auxiliar chamado x d , com tamanho compatível ao vetor d i d x :

A linha de código acima diz que o vetor x d é um pedaço do vetor x , começando do segundo elemento de x e indo até o final de x (indicando por e n d ). Precisamos criá-lo pois o vetor d i d x tem um elemento a menos que o vetor x e para calcular d 2 i d x 2 , precisamos que os vetores d 2 i e d x 2 tenham o mesmo comprimento.

Para criar o vetor d x 2 , digite a linha de código:

O vetor d x 2 contém a diferença entre os elementos adjacentes de x d e representa o vetor d x 2 .

Passo 6

Com os vetores d x 2 e d 2 i criados, podemos calcular d ² i d x ² por meio da linha de código:

Com este comando, dividimos cada elemento do vetor d 2 i pelo elemento do vetor d x 2 que esteja na mesma posição e o resultado é armazenado no vetor d 2 i d x 2 .

O vetor d 2 i d x 2 representa a derivada segunda de i ( x ) obtida por meio de diferenciação numérica. Com o vetor d 2 i d x 2 , podemos gerar o gráfico de d ² i d x ² .

Passo 7

Antes de gerar o gráfico de i ( x ) , d i d x e de d ² i d x ² , precisamos criar um vetor auxiliar para podermos plotar a curva de d ² i d x ² em função de x .

Precisamos criar esse vetor auxiliar porque o vetor d 2 i d x 2 tem dois elementos a menos do que x , já que ele na prática foi criado usando a função d i f f ( ) duas vezes seguidas. Vetores de tamanhos diferentes dão um erro na função p l o t ( ) .

Vamos chamar o vetor auxiliar da segunda derivada de x d 2 e criá-lo com a linha de código:

Este comando diz que o vetor x d 2 é um pedaço do vetor x , começando do terceiro elemento de x e indo até o final de x .

Note que, para plotar d i d x em função de x , podemos aproveitar o vetor x d do passo 5, já x d tem o mesmo comprimento de   d i d x .

Pronto! Já temos todas informações necessárias para gerar o gráfico pedido no enunciado.

Passo 8

Vamos criar as curvas de i ( x ) , de d i d x e de d ² i d x ² na mesma janela. Para isso, entre as três linhas de código abaixo:

Na primeira linha, pedimos ao MATLAB para plotar i em função de x , d i d x em função de x d e d 2 i d x 2 em função de x d 2 .

Na segunda linha, damos um nome ao eixo x do gráfico: chamamos ele de x.

Na terceira linha, criamos uma legenda para o gráfico. A string ‘ i ( x ) ’ é a legenda da curva gerada pelo primeiro par de vetores, x e i , da função p l o t ( ) . Já a string ‘ d i / d x ’ é a legenda da curva gerada pelo segundo par de vetores, x d e d i d x , da função p l o t ( ) . Finalmente, a string ‘ d 2 i / d x 2 ’ se refere ao terceito par de vetores da função p l o t ( ) , x d 2 e d 2 x d x 2 .

Rodando nosso programa, temos o gráfico pedido no enunciado:

A curva azul representa i ( x ) , a curva vermelha representa d i d x e a curva amarela representa d ² i d x ² .

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #3

“Adaptado de UFRJ – Lista 3 – Computação Científica”

Desenvolva um código que permita localizar o mínimo da função y = 2 x + 5 x 2 + 5 . Considere um intervalo de [-5, 5] e use diferenciação numérica.

Passo 1

A questão pede para localizarmos o mínimo de uma função usando diferenciação numérica.

Para encontrarmos o mínimo de uma função, temos que relembrar o conteúdo de derivadas de Cálculo 1.

No ponto mínimo de uma função, a primeira derivada é zero. É um ponto onde a tangente é representada por uma linha horizontal.

Entretanto, pontos máximos de função também tem a primeira derivada igual a zero. Para confirmar se um ponto onde a primeira derivada é igual a 0 é um ponto de mínimo ou máximo, devemos calcular a segunda derivada neste ponto. Se a derivada segunda for positiva, o ponto é um local de mínimo.

Logo, para este exercício, vamos determinar a primeira e a segunda derivadas de y = 2 x + 5 x 2 + 5 , por meio de diferenciação numérica, para x indo de -5 a 5. Em seguida, vamos achar o valor de x em que a primeira derivada d y d x é nula, e o chamaremos de x m i n . Então, vamos calcular a segunda derivada d ² y d x ² em x m i n , para ver se resulta em um valor positivo ou negativo e termos certez que se trata de um ponto mínimo.

Ao final, para termos as coordenadas do ponto mínimo, substituímos x m i n em y = 2 x + 5 x 2 + 5 e encontramos y m i n .

Passo 2

Primeiramente, vamos criar dois vetores, um representando o intervalo de x pedido no enunciado e outro com a função y , calculada para cada elemento do vetor x .

Crie um script novo no MATLAB e digite as duas linhas de código:

Na primeira linha, foi criado um vetor x que vai de -5 a 5, a um passo de 0,01. Eu escolhi este passo para ter um pouco mais de precisão no resultado, mas você pode escolher o passo que quiser.

Na segunda linha, calculamos a função y para cada elemento do vetor x , por isso temos o ponto ao lado de x . Por exemplo, o comando x . ^ 2 elevada cada elemento de x ao quadrado. O resultado é armazenado no vetor y , que tem o mesmo comprimento de x .

Passo 3

Depois de criarmos os vetores x e y , podemos determinar as derivadas primeira e segunda de y . Vamos começar com a a derivada primeira. Para encontrarmos d y d x por diferenciação numérica, temos que gerar dois vetores, um representando d y e outro representando d x . O vetor d y teria a diferença de y de um valor de x a outro e o vetor d x teria a diferença entre um valor de x e outro.

Estes vetores são gerados por meio da função d i f f ( ) , que tem a seguinte estrutura:

Y   =   d i f f ( X ,   n )

Ela calcula n   vezes a diferença entre os elementos adjacentes do vetor X e nos dá o resultado na forma do vetor Y .

Os dois vetores são gerados por meio das seguintes linhas de código:

Na primeira linha, é criado o vetor d x , que contém as diferenças entre elementos adjacentes do vetor x . Para criar o vetor d x , a funçao d i f f ( ) faz um elemento de x menos o elemento à esquerda, começando a partir do segundo elemento de x .

Na segunda linha, é feita a mesma coisa, mas com o vetor y . A variação de y é armazenada no vetor d y .

Note que não entramos nenhum valor para n , porque queremos que a diferença seja feita uma vez. Quando não entramos com nenhum valor para n na função d i f f ( ) , por o padrão o MATLAB adota n = 1 .

Passo 4

Com os vetores d x e d y criados, podemos calcular d y d x por meio da linha de código:

Com este comando, dividimos cada elemento do vetor d y pelo elemento do vetor d x que esteja na mesma posição e o resultado é armazenado no vetor d y d x .

O vetor d y d x representa a derivada primeira de y obtida por meio de diferenciação numérica. Com o vetor d y d x , podemos calcular a derivada segunda d ² y d x ² .

Passo 5

Após determinarmos a primeira derivada, vamos calcular a segunda derivada de y , por meio de diferenciação numérica. Assim como fizemos para a primeira derivada no passo 3, para determinar d 2 y d x 2 , precisamos construir dois vetores, um representando d 2 y e outro representando d x 2 , e dividir um pelo outro.

Para isto, usamos a função d i f f ( ) de novo. No MATLAB, digite a linha de código:

Com este comando, aplicamos a função d i f f ( ) no vetor d y d x , que representa d y d x , e armazenamos o resultado no vetor d 2 y . Calculando a diferença entre os elementos adjacentes de d y d x , é como se estivéssemos calculando a derivada de d y d x , que é consequentemente d 2 y d x 2 .

Para criar o vetor d x 2 , vamos criar um vetor auxiliar chamado x d , com tamanho compatível ao vetor d y d x :

A linha de código acima diz que o vetor x d é um pedaço do vetor x , começando do segundo elemento de x e indo até o final de x (indicando por e n d ). Precisamos criá-lo pois o vetor d y d x tem um elemento a menos que o vetor x e para calcular d 2 y d x 2 , precisamos que os vetores d 2 y e d x 2 tenham o mesmo comprimento.

Para criar o vetor d x 2 , digite a linha de código:

O vetor d x 2 contém a diferença entre os elementos adjacentes de x d e representa o vetor d x 2 .

Passo 6

Com os vetores d x 2 e d 2 y criados, podemos calcular d ² y d x ² por meio da linha de código:

Com este comando, dividimos cada elemento do vetor d 2 y pelo elemento do vetor d x 2 que esteja na mesma posição e o resultado é armazenado no vetor d 2 y d x 2 .

O vetor d 2 y d x 2 representa a derivada segunda de y obtida por meio de diferenciação numérica.

A partir de d x d y e d 2 y d x 2 , podemos encontrar o ponto mínimo de y .

Passo 7

Em um ponto de mínimo, d y d x = 0 . Por isso, temos que encontrar o elemento do vetor d y d x que seja igual a 0 e sua posição, e ver qual elemento do vetor x d está na mesma posição. Este elemento de x d será a coordenada x do ponto mínimo da função, isto é, x m i n .

Vale destacar que usamos o vetor x d e não o vetor x . Se usarmos o vetor x para encontrar x m i n , x m i n não estará exatamente na mesma posição do elemento nulo de d y d x , pois o vetor x tem um elemento a mais do que d y d x .

Contudo, como calculamos d y d x por diferenciação numérica, dificilmente o vetor d y d x terá um elemento exatamente igual a 0. Por isto, devemos encontrar o elemento de d y d x que seja o mais próximo possível de 0. Para encontrarmos este valor, usaremos a função m i n ( ) do MATLAB, que tem a seguinte estrutura:

[ m i n i m o , i n d i c e ]   =   m i n ( X )

Na função m i n ( ) , entramos com um vetor X e ela nos retorna o menor elemento de X , representado por m i n i m o , e a posição onde ele se encontra em X , representado por i n d i c e .

Para encontrar o elemento mais próximo de 0 em dydx, entre com a linha de código:

Com o comando a b s ( 0 - d y d x ) dentro da função m i n ( ) , criamos um vetor que contém o valor absoluto da diferença entre 0 e cada elemento de d y d x . Em seguida, a função m i n ( ) vai procurar o menor elemento deste vetor resultante e vai armazenar seu valor na variável e r r o e sua posição na variável i n d i c e .

A posição do menor elemento do vetor a b s ( 0 - d y d x ) nos indica a posição do elemento de d y d x que é mais próxima de 0 e a posição de x m i n no vetor x d .

Passo 8

Vamos verificar se o elemento de dydx na posição indice realmente está próximo de 0? Para isto, entre com o comando:

Este comando armazena na variável d 0 o elemento de d y d x que se encontra na posição indice.

Para encontrar x m i n , digite a linha de código:

Com este comando, o elemento de x d na posição i n d i c e é armazenado na variável x _ m i n . x _ m i n é para ser a coordenada x do ponto mínimo de y .

Se você rodar o programa que temos até agora e pedir para ver d 0 e x _ m i n , você terá estes resultados:

O valor mais próximo de 0 de d y d x é -0,05 e x m i n = - 0,2 .

Para nos certificarmos que x _ m i n é mesmo uma das coordenadas do ponto mínimo, vamos ver o valor da segunda derivada no vetor d 2 y d x 2 que se encontra na mesma posição de x _ m i n . Contudo, como d 2 y d x 2 tem um elemento a menos do x d e d y d x , não podemos usar diretamente o valor de i n d i c e . Temos que subtrair 1 de i n d i c e para encontrar o valor que queremos:

Nesta linha de código, o elemento do vetor d 2 y d x 2 que se encontra na posição i n d i c e - 1 é armazenado em d 2 .

Para que x _ m i n seja a coordenada x de um ponto de mínimo, d 2 deve ser positivo. Rodando o programa de novo e pedindo pra ver d 2 , temos:

Como d 2   é positivo, x _ m i n realmente é uma das coordenadas do ponto mínimo.

Passo 9

Para encontrar a coordenada em y do ponto mínimo, substituímos x _ m i n na função y = 2 x + 5 x 2 + 5 com a seguinte linha de código:

O resultado é armazenado em y _ m i n e representa a coordenada em y do ponto mínimo. Rodando o programa novamente e imprimino y _ m i n , temos:

Resposta

O ponto mínimo de y = 2 x + 5 x 2 + 5 é x m i n y m i n = ( - 0,2 4,8   )

Exercício Resolvido #4

“Adaptado de Numerical Methods in Engineering with Matlab, de Jaan Kiusalaas (Pennsylvania State University), 1ª edição (2005), p. 197, exercício 12.”

A figura abaixo mostra um mecanismo biela-manivela:

A manivela AB tem comprimento R   = 90 mm e rotaciona a uma velocidade constante. A posição x do pistão C varia de acordo com o ângulo θ segundo a equação:

x = R c o s c o s   θ   + 2,5 2 - s i n s i n   θ   2

Crie um programa que calcule a taxa de variação da posição do pistão em função de θ , para θ = 0 ° ,   5 ° ,   10 ° ,   … ,   180 ° , usando diferenciação numérica. Ao final, plote as curvas de x em função de θ e de d x d θ em função de θ .

Passo 1

O enunciado nos dá um expressão de x   em função de θ , representando a posição de um pistão de um mecanismo biela-manivela.

Ele pede para encontrarmos a taxa de variação da posição do pistão em função de θ . Isto significa que devemos encontrar a primeira derivada de x em função de θ , isto é, d x d θ .

Para encontrarmos d x d θ por diferenciação numérica, primeiramente devemos calcular o valor de x para a faixa de valores de θ dada, que vai de 0° a 180°, de 5° em 5°. Em seguida, usamos a função d i f f ( ) do MATLAB nos valores encontrados para determinar d x d θ .

Ao final, geraremos um gráfico com as curvas de x   e d x d θ   em função de θ .

Passo 2

Primeiramente, crie um script novo no MATLAB e digite o código abaixo, para gerar um vetor contendo o intervalo de θ pedido no enunciado:

O comando acima cria um vetor chamado t h e t a cujos elementos vão de 0° a 180°, com um passo de 5°, conforme exigido no enunciado. Os elementos de t h e t a são convertidos de graus para radianos ao serem multiplicados por π 180 .

Em seguida, precisamos calcular x para cada elemento do vetor t h e t a . Para isso, usaremos um laço f o r . Em seu script do MATLAB, digite as linhas de código:

Na primeira linha, eu entro com o comprimento da manivela AB, que é de 90 mm, armazenando-a em uma variável chamada R .

Na segunda linha, crio um vetor x que só tem zeros, com a função z e r o s ( ) , que tem a seguinte estrutura:

A   =   z e r o s ( n _ l i n h a s ,   n _ c o l u n a s )

A função z e r o s ( ) cria uma matriz A que só tem 0 em seus elementos. Ela tem como entrada o número de linhas da matriz de zeros que você quer criar, n _ l i n h a s , e o número de colunas, n _ c o l u n a s .

O vetor x criado na segunda linha tem uma linha e o mesmo número de colunas do vetor t h e t a . Entramos com o número de colunas de t h e t a usando a função l e n g t h ( ) , que nos dá a quantidade de elementos de t h e t a .

Na terceira linha, começo com meu laço f o r . Ele vai de 1 até a quantidade de elementos de t h e t a , determinada pela função l e n g t h ( ) .

Na quarta linha, entro com a função que determina a posição do pistão em função de θ .

Finalmente, na última linha, encerro o laço f o r .

Passo 3

Para encontrarmos d x d θ por diferenciação numérica, temos que gerar dois vetores, um representando d x e outro representando d θ . O vetor d x teria a diferença de posição do pistão de um ângulo θ a outro e o vetor d θ teria a diferença entre um ângulo θ e outro.

Estes vetores são gerados por meio da função d i f f ( ) . Lembrando que ela tem a seguinte estrutura:

Y   =   d i f f ( X ,   n )

Ela calcula n   vezes a diferença entre os elementos adjacentes do vetor X e nos dá o resultado na forma do vetor Y .

Os dois vetores são gerados por meio das seguintes linhas de código:

Na primeira linha, é criado o vetor d x , que contém as diferenças entre elementos adjacentes do vetor x . Para criar o vetor d x , a funçao d i f f ( ) faz um elemento de x menos o elemento à esquerda, começando a partir do segundo elemento de x .

Na segunda linha, é feita a mesma coisa, mas com o vetor t h e t a . A variação de t h e t a é armazenada no vetor d t h e t a .

Note que não entramos nenhum valor para n , porque queremos que a diferença seja feita uma vez. Quando não entramos com nenhum valor para n na função d i f f ( ) , por o padrão o MATLAB adota n = 1 .

Passo 4

Com os vetores d x e d t h e t a criados, podemos calcular d x d θ por meio da linha de código:

Com este comando, dividimos cada elemento do vetor d x pelo elemento do vetor d t h e t a que esteja na mesma posição e o resultado é armazenado no vetor d x d t h e t a .

O vetor d x d t h e t a representa a derivada de x em função de θ obtida por meio de diferenciação numérica. Em outras palavras, d x d t h e t a representa a taxa de variação da posição do pistão de acordo com o ângulo θ .

Com o vetor x e d x d t h e t a , podemos gerar os gráficos pedidos no enunciado.

Passo 5

Antes de gerar o gráfico de x e de d x d θ em função de θ , precisamos criar um vetor auxiliar para podermos plotar a curva de d x d θ . Esse vetor auxiliar é necessário por que o vetor d x d t h e t a tem um elemento a menos do que t h e t a , o que levaria a um erro na função p l o t ( ) .

Vamos chamar o vetor auxiliar de t d e criá-lo da seguinte forma:

A linha de código acima diz que o vetor t d é um pedaço do vetor t h e t a , começando do segundo elemento de t h e t a e indo até o final de t h e t a (indicando por e n d ).

Já temos tudo o que precisamos para gerar os gráficos de x e de d x d θ . Vamos criar as curvas de ambos na mesma janela. Para isso, entre as três linhas de código abaixo:

Na primeira linha, pedimos ao MATLAB para plotar x em função de t h e t a e d x d t h e t a em função de t d .

Na segunda linha, damos um nome ao eixo x do gráfico: chamamos ele de θ e indicamos a unidade entre colchetes. Usei \ t h e t a para sair o símbolo θ no gráfico.

Na terceira linha, criamos uma legenda para o gráfico. A string ‘ x ’ é a legenda da curva gerada pelo primeiro par de vetores, t h e t a e x , da função p l o t ( ) . Já a string ‘ d x / d \ t h e t a ’ é a legenda da curva gerada pelo segundo par de vetores, t d e d x d t h e t a , da função p l o t ( ) . Novamente, usei \ t h e t a para sair o símbolo θ no gráfico.

Ao rodarmos o programa, é gerado o gráfico abaixo:

A curva azul representa a posição x do pistão em função de θ .

A curva vermelha representa a taxa de variação da posição do pistão em função de θ , isto é, d x d θ .

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #5

“Adaptado de UNICAMP - Exercícios de Cálculo Numérico - Prof. R. Biloti - 29.04.2021. Exercício 3.5”

Usando os dados da tabela a seguir, estime f ' ( 0,6 ) e f ’ ’ ( 0,6 )

Passo 1

A questão nos pede para estimar a primeira e a segunda derivadas de f ( x ) em x = 0,6 , a partir dos dados da tabela.

Para resolvermos o exercício, geraremos um gráfico com três curvas, uma representando f ( x ) , outra representando f ' ( x ) e outra representando f ' ' ( x ) , com x indo de 0,2 a 1 . Faremos a estimativa de f ' ( 0,6 ) e f ’ ’ ( 0,6 ) a partir do gráfico, procurando o ponto nas curvas de f ' ( x ) e f ' ' ( x ) que tenha como coordenada x = 0,6 .

Para gerarmos as curvas com função p l o t ( ) , precisamos calcular as derivadas de f ( x ) a partir da tabela, usando diferenciação numérica. Para isso, usaremos a função d i f f ( ) do MATLAB. Lembrando que ela tem a estrutura:

Y   =   d i f f ( X ,   n )

Ela calcula n   vezes a diferença entre os elementos adjacentes do vetor X e nos dá o resultado na forma do vetor Y .

Para encontrarmos a derivada primeira, o vetor X   de entrada de d i f f ( ) será a função f ( x ) . Para a derivada segunda, o vetor X será f ' ( x ) .

Passo 2

Primeiramente, crie um script novo no MATLAB e entre com os dados da tabela:

O vetor x contém a primeira linha da tabela e o vetor f , a segunda linha. Desta forma, o par de vetores x e f representa f ( x ) .

Depois de criarmos os vetores x e f , podemos determinar as derivadas primeira e segunda de f ( x ) . Vamos começar com a a derivada primeira. Para encontrarmos f ' x = d f d x por diferenciação numérica, temos que gerar dois vetores, um representando d f e outro representando d x . O vetor d f teria a diferença de f ( x ) de um valor de x a outro e o vetor d x teria a diferença entre um valor de x e outro.

Estes vetores são gerados por meio da função d i f f ( ) , que tem a estrutura:

Y   =   d i f f ( X ,   n )

Ela calcula n   vezes a diferença entre os elementos adjacentes do vetor X e nos dá o resultado na forma do vetor Y . Como queremos que a diferença seja feita somente uma vez neste exercício, tanto para calcular a derivada primeira quanto a segunda, não precisamos entrar com nenhum valor para n na função d i f f ( ) , pois por padrão o MATLAB adota n = 1 quando a entrada n não é especificada.

Os dois vetores são gerados por meio das seguintes linhas de código:

Na primeira linha, é criado o vetor d x , que contém as diferenças entre elementos adjacentes do vetor x . Para criar o vetor d x , a funçao d i f f ( ) faz um elemento de x menos o elemento à esquerda, começando a partir do segundo elemento de x .

Na segunda linha, é feita a mesma coisa, mas com o vetor f . A variação de f é armazenada no vetor d f .

Com os vetores d x e d f criados, podemos calcular d f d x por meio da linha de código:

Com este comando, dividimos cada elemento do vetor d f pelo elemento do vetor d x que esteja na mesma posição e o resultado é armazenado no vetor d f d x .

O vetor d f d x representa a derivada primeira de f ( x ) obtida por meio de diferenciação numérica. Com o vetor d f d x , podemos gerar o gráfico de f ' ( x ) .

Passo 3

Após determinarmos f ' ( x ) , podemos calcular f ' ' ( x ) , por meio de diferenciação numérica. Assim como fizemos para a primeira derivada no passo 2, para determinar f ' ' x = d 2 f d x 2 , precisamos construir dois vetores, um representando d 2 f e outro representando d x 2 , e dividir um pelo outro.

Para isto, usamos a função d i f f ( ) de novo. No MATLAB, digite a linha de código:

Com este comando, aplicamos a função d i f f ( ) no vetor d f d x , que representa f ' x = d f d x , e armazenamos o resultado no vetor d 2 f . Calculando a diferença entre os elementos adjacentes de d f d x é como se estivéssemos calculando a derivada de f ' ( x ) , que é consequentemente f ' ' ( x ) .

d 2 f é o nosso vetor representando d 2 f . Para criar o vetor d x 2 , vamos criar um vetor auxiliar chamado x d , com tamanho compatível ao vetor d f d x :

A linha de código acima diz que o vetor x d é um pedaço do vetor x , começando do segundo elemento de x e indo até o final de x (indicando por e n d ). Precisamos criá-lo pois o vetor d f d x tem um elemento a menos que o vetor x e para calcular d 2 f d x 2 , precisamos que os vetores d 2 f e d x 2 tenham o mesmo comprimento.

Para criar o vetor d x 2 , digite a linha de código:

O vetor d x 2 contém a diferença entre os elementos adjacentes de x d e representa o vetor d x 2 .

Com os vetores d x 2 e d 2 f criados, podemos calcular f ' ' x = d ² f d x ² por meio da linha de código:

Com este comando, dividimos cada elemento do vetor d 2 f pelo elemento do vetor d x 2 que esteja na mesma posição e o resultado é armazenado no vetor d 2 f d x 2 .

O vetor d 2 f d x 2 representa f ' ' ( x ) obtido por meio de diferenciação numérica. Com o vetor d 2 f d x 2 , podemos gerar o gráfico de f ' ' ( x ) .

Passo 4

Antes de gerar o gráfico de f ( x ) , f ' ( x ) e de f ' ' ( x ) , precisamos criar um vetor auxiliar para podermos plotar f ' ' ( x ) em função de x .

Precisamos criar esse vetor auxiliar porque o vetor d 2 f d x 2 tem dois elementos a menos do que x , já que ele na prática foi criado usando a função d i f f ( ) duas vezes seguidas. Vetores de tamanhos diferentes dão um erro na função p l o t ( ) .

Vamos chamar o vetor auxiliar de f ’ ’ ( x ) de x d 2 e criá-lo com a linha de código:

Este comando diz que o vetor x d 2 é um pedaço do vetor x , começando do terceiro elemento de x e indo até o final de x .

Note que, para plotar f ' ( x ) em função de x , podemos aproveitar o vetor x d do passo 3, já que x d tem o mesmo comprimento de   d f d x .

Para plotar f ( x ) , f ' ( x ) e f ' ' ( x ) na mesma janela, digite as três linhas de código abaixo:

Na primeira linha, pedimos ao MATLAB para plotar f em função de x , d f d x em função de x d e d 2 f d x 2 em função de x d 2 .

Na segunda linha, damos um nome ao eixo x do gráfico: chamamos ele de x .

Na terceira linha, criamos uma legenda para o gráfico. A string ‘ f ( x ) ’ é a legenda da curva gerada pelo primeiro par de vetores, x e f , da função p l o t ( ) . Já a string ‘ d f / d x ’ é a legenda da curva gerada pelo segundo par de vetores, x d e d f d x , da função p l o t ( ) . Finalmente, a string ‘ d ^ 2 f / d x ^ 2 ’ se refere ao terceito par de vetores da função p l o t ( ) , x d 2 e d 2 f d x 2 .

Rode o programa para ver o gráfico:

A curva azul representa f ( x ) , a curva vermelha é f ’ ( x ) e a curva amarela, f ’ ’ ( x ) . Para estimar f ' ( 0,6 ) e f ’ ’ ( 0,6 ) , clique sobre as curvas vermelha e amarela, respectivamente, e procure o ponto com coordenada X = 0,6 nas duas curvas (como no print acima). A coordenada Y desses pontos são a estimativa de f ' ( 0,6 ) e f ’ ’ ( 0,6 ) .

Resposta

f ' 0,6 = 53,85

f ’ ’ 0,6 = 191,8

Exercício Resolvido #6

Adaptado de “Numerical Methods in Engineering with Matlab”, de Jaan Kiusalaas (Pennsylvania State University), 1ª edição (2005), p. 190, exemplo 5.3.

O mecanismo de quatro barras mostrado acima tem as dimensões a = 100   m m , b = 120   m m , c = 150   m m e d = 180   m m . Pode ser mostrado por geometria que a relação entre os ângulos α e β é

Para um dado valor de α , podemos resolver esta equação transcendental para β por algum método de determinação de raízes. Fazendo isso com α   =   0 ° ,   5 ° ,   10 ° ,   .   .   .   ,   30 ° , temos os resultados

Se o elo A B gira com a velocidade angular constante de 25   r a d / s , use diferenciação numérica para tabular a velocidade angular d β / d t do elo B C em relação a α .

Passo 1

O enunciado nos dá uma tabela de β em função de α , o que nos permite calcular d β d α por meio de diferenciação numérica com o comando d i f f ( ) do MATLAB. Contudo, o exercício pede para encontrarmos d β d t para cada valor de α .

Para encontrar d β d t , o enunciado nos informa que d α d t = 25   r a d / s . Com esse dado, podemos obter d β d t a partir de d β d α e d α d t , usando o seguinte raciocínio:

d β d t = d β d α ∙ d α d t = 25 d β d α

Logo, para calcularmos d β d t , primeiramente calculamos d β d α usando o comando d i f f ( ) e, em seguida, multiplicamos o resultado por d α d t . Desta forma, temos d β d t para cada valor de α .

Passo 2

Vamos começar calculando d β d α . Para isto, devemos entrar os valores da tabela do enunciado no MATLAB. Em um script novo, crie dois vetores, um para cada linha da tabela:

O vetor a l p h a contém os valores da primeira linha da tabela, sendo convertidos de graus para radianos, por meio da multiplicação por π 180 . Já o vetor b e t a contém os valores da segunda linha da tabela, que já são dados em radianos.

Depois de criarmos os vetores a l p h a e b e t a , podemos determinar d β d α por diferenciação numérica. Para isto, temos que gerar dois vetores, um representando d β e outro representando d α . O vetor d β teria a diferença de β de um valor de α a outro e o vetor d α teria a diferença entre um valor de α e outro.

Estes vetores são gerados por meio da função d i f f ( ) , que tem a estrutura:

Y   =   d i f f ( X ,   n )

Ela calcula n   vezes a diferença entre os elementos adjacentes do vetor X e nos dá o resultado na forma do vetor Y . Como queremos que a diferença seja feita somente uma vez, não precisamos entrar com nenhum valor para n na função d i f f ( ) , pois por padrão o MATLAB adota n = 1 quando a entrada n não é especificada.

Os dois vetores são gerados por meio das seguintes linhas de código:

Na primeira linha, é criado o vetor d a , que contém as diferenças entre elementos adjacentes do vetor a l p h a , logo, ele representa d α . Para criar o vetor d a , a funçao d i f f ( ) faz um elemento de a l p h a menos o elemento à esquerda, começando a partir do segundo elemento de a l p h a .

Na segunda linha, é feita a mesma coisa, mas com o vetor b e t a . A variação de b e t a é armazenada no vetor d b , que representa d β .

Passo 3

Com os vetores d a e d b criados, podemos calcular d β d α por meio da linha de código:

Com este comando, dividimos cada elemento do vetor d b pelo elemento do vetor d a que esteja na mesma posição e o resultado é armazenado no vetor d b d a .

O vetor d b d a representa d β d α obtida por meio de diferenciação numérica. A partir deste vetor, podemos calcular d β d t usando d α d t = 25   r a d / s .

Passo 4

Para calcular d β d t , multiplicamos o vetor d b d a por d α d t = 25   r a d / s . Por isso, vamos entrar com d α d t no MATLAB e em seguida realizar a multiplicação:

A variável d a d t represente d α d t = 25   r a d / s e na linha seguinte, ela multiplica d b d a para obter d β d t para cada valor de α , o que é armazenado em d b d t .

Os valores de d b d t representam d β d t para cada valor de α a partir de 5 ° , pois acabamos “perdendo” o primeiro elemento do vetor a l p h a ao aplicar o comando d i f f ( ) .

O vetor d b d t é o resultado do exercício:

Resposta

Exercício Resolvido #7

Adaptado de “Numerical Methods in Engineering with Matlab”, de Jaan Kiusalaas (Pennsylvania State University), 1ª edição (2005), p. 197, exercício 13.

As estações de radar A e B , separadas pela distância a = 500   m , rastreiam o avião C registrando os ângulos α e β em intervalos de um segundo. Se três leituras sucessivas forem

calcule a velocidade v do avião e o ângulo de subida γ em t = 10   s . As coordenadas do avião são calculadas como

Passo 1

Para resolvermos o exercício, usaremos os valores de α e β da tabela para calcular as coordenadas x e y do avião, para cada um dos três instantes de tempo 9 ,   10 e 11   s . Com as coordenadas x e y para cada instante de tempo, podemos usar o comando d i f f ( ) do MATLAB para obter, por meio de derivação numérica, as componentes horizontal e vertical da velocidade do avião, dadas por v x = d x / d t e v y = d y / d t , respectivamente.

Com v x e v y em t = 10   s , podemos calcular a velocidade v do avião, dada por:

v = v x 2 + v y 2

Já o ângulo γ é dado pelo arcotangente de v y e v x em t = 10   s :

γ = tan - 1 ⁡ v y v x

Passo 2

Vamos começar inserindo os dados fornecidos pelo enunciado. Em um novo script, entre com a distância a e os dados da tabela:

A primeira linha da tabela, que contém os instantes de tempo, é representada pelo vetor t .

Os ângulos α e β da tabela são armazenados nos vetores a l p h a e b e t a , respectivamente. Os ângulos são convertidos de graus para radianos, por meio da multiplicação por π / 180 . Fazemos a conversão pois calcularemos as tangentes usando o comando t a n do MATLAB, cuja entrada deve ser um ângulo em radianos.

Com os dados do enunciados implementados em nosso script, podemos calcular as coordenadas x e y do avião para cada um dos três instantes de tempo, usando as equações fornecidas pelo enunciado:

Note que, como a l p h a e b e t a são vetores, o resultado de t a n ( a l p h a ) e t a n ( b e t a ) também serão vetores, por isso, para realizarmos a multiplicação e a divisão nas equações das coordenadas do avião, devemos usar . / e . * , para fazer a operação entre cada elemento dos vetores.

A posição em x e em y do avião calculada a cada instante é armazenada nos vetores x e y , respectivamente. Esses vetores têm 3 elementos, representando a posição nos instantes 9 ,   10 e 11   s .

Passo 3

Depois de calcularmos os vetores x e y , podemos determinar as componentes horizontal e vertical da velocidade do avião por meio de diferenciação numérica, calculando a derivada das posições x e y em relação ao tempo t . Para encontrarmos d x d t e d y d t por diferenciação numérica, temos que gerar três vetores, um representando d x , outro representando d y e outro representando d t . Os vetores d x e d y teriam a diferença das posições x e y de instante de tempo t a outro, respectivamente. Já o vetor d t teria a diferença entre um instante de tempo t e outro.

Estes vetores são gerados por meio da função d i f f ( ) , que tem a estrutura:

Y   =   d i f f ( X ,   n )

Ela calcula n   vezes a diferença entre os elementos adjacentes do vetor X e nos dá o resultado na forma do vetor Y . Como queremos que a diferença seja feita somente uma vez, não precisamos entrar com nenhum valor para n na função d i f f ( ) , pois por padrão o MATLAB adota n = 1 quando a entrada n não é especificada.

Os três vetores são gerados por meio das seguintes linhas de código:

Na primeira linha, é criado o vetor d t , que contém as diferenças entre elementos adjacentes do vetor t . Para criar o vetor d t , a funçao d i f f ( ) faz um elemento de t menos o elemento à esquerda, começando a partir do segundo elemento de t .

Na segunda e na terceira linha, é feita a mesma coisa, mas com os vetores x e y . A variação de x é armazenada no vetor d x e a de y , em d y .

Com os vetores d t , d x e d y criados, podemos calcular d x d t e d y d t por meio das linhas de código:

Com estes comandos, dividimos cada elemento do vetor d x e d y pelo elemento do vetor d t que esteja na mesma posição e os resultados são armazenados nos vetores d x d t e d y d t .

O vetor d x d t representa a derivada da posição x do avião em relação ao tempo, indicando, portanto, a componente horizontal da velocidade do avião. Já o vetor d y d t representa a derivada da posição y do avião em relação ao tempo, indicando a componente vertical da velocidade do avião.

Passo 4

O exercício pede para calcular a velocidade v do avião e o ângulo de subida γ em t = 10   s . As componentes horizontal e vertical da velocidade v em t = 10   s são os primeiros elementos dos vetores d x d t e d y d t , respectivamente. Vamos armazená-los nas variáveis v x e v y , para facilitar o cálculo da resposta do exercício:

Com v x e v y , podemos calcular a velocidade v do avião, dada por:

v = v x 2 + v y 2

Por isso, implemente em seu programa a linha de código:

A velocidade v do avião é obtida ao executar o programa, dada pela variável v , que é igual a:

Passo 5

O ângulo γ é dado pelo arcotangente de v y e v x em t = 10   s :

γ = tan - 1 ⁡ v y v x

Para calcular o arcotangente, usaremos a função a t a n 2 , que retorna o ângulo considerando os quatro quadrantes do círculo trigonométrico. a t a n 2 tem como sintaxe:

P = a t a n 2 ( Y , X )

Onde Y e X são números reais, representando as coordenadas de um ponto no círculo trigonométrico, e P é o ângulo em radianos. a t a n 2 calcula o arcotangente da razão Y / X .

Por isso, inclua em seu programa a linha de código:

Com este comando, eu calculo o arcotangente de v y v x e converto o resultado de radianos para graus, por meio da multiplicação por 180 / π . O ângulode subida do avião é armazenado em g a m m a .

Rodando o programa, temos que g a m m a é igual a:

Resposta

v = 50 , 4181   m / s

γ = 15 , 5248 °