Integrais Numéricas
Produzido por Gustavo BarbosaTeoria
Introdução
E aí, pessoal, tudo bem?
Já pararam para pensar como os pilotos de foguetes sabem a velocidade do veículo que eles estão pilotando? Não tem como eles saírem do foguete e medir a velocidade lambendo a ponta do dedo e pondo a mão para o alto, né?
Acredita que, com o que você aprendeu em Cálculo 1 e Cálculo Numérico, você já consegue entender como se calcula a velocidade de um foguete?
Mas antes de vermos como os engenheiros da NASA calculam a velocidade dos foguetes, vamos relembrar rapidamente o que é uma integral e como podemos calculá-la no MATLAB. Vai anotando tudo aí, que depois desta aula você vai se sentir um pouquinho mais perto de trabalhar na sala de operações da NASA.

O que significa uma integral
Lembrando das aulinhas de Cálculo 1, a integral de uma função no intervalo corresponde à área sob a curva , entre os pontos e :
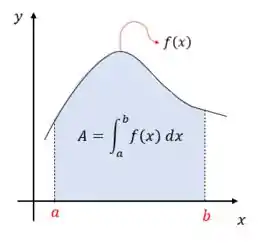
Se resolvermos essa integral usando as regrinhas e as integrais de cada função, chegamos à solução analítica da integral, que corresponde ao valor exato da área sob a curva.
Mas as vezes o cálculo dessa integral é muito trabalhoso ou é impossível, nesses casos podemos usar um método numérico para encontrar um valor aproximado dessa área.
No MATLAB, podemos calcular a integral de uma função dentro de um intervalo definido com a função , que usa o método dos trapézios para calcular a integral de uma função.
Neste método, a área sob a curva é dividida em vários trapézios, a área de cada trapézio é calculada e então somadas para obtermos a área total sob curva. A figura abaixo pode ajudar a entender esse método:
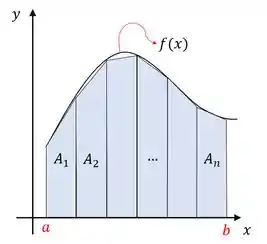
Vale ressaltar que esse é um método numérico e a área que encontramos é um valor aproximado. Por isso, em quanto mais trapézios dividirmos a área sob a curva, mais preciso é o resultado dessa integração numérica.
A função tem a seguinte estrutura:
Ela nos retorna o resultado da integração, que representa a área sob a curva , definida no intervalo .
Bora ver um exemplo para entender como o funciona. Digamos que eu queira integrar no MATLAB, usando o método do trapézio, a seguinte função:
Quero fazer essa integração para um intervalo de 0 a 50 (), dividindo este intervalo em pedacinhos de . No MATLAB, isto ficaria assim:

Primeiro, criamos o vetor , que vai de a , com um passo de . Em seguida, calculamos para cada valor de e armazenamos o resultado no vetor . Com isto, já temos as duas entradas para a função e podemos fazer a integração numérica da função para o intervalo , isto é, encontrar a área embaixo da curva neste intervalo.
Só por curiosidade, este é o resultado =)
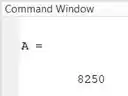
Lembra que eu disse que quanto mais trapézios tivermos sob a curva, maior é a precisão do resultado? Para termos mais trapézios, temos que diminuir o comprimento dos pedacinhos em que dividimos o intervalo . Se em vez de eu usar um passo igual a na integração e usar um passo igual a , o vetor fica assim:
![]()
E temos um resultado ligeiramente diferente:
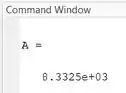
Este resultado deve estar mais próximo da área real. Por isso, preste atenção ao passo que for usar na hora de resolver os problemas.
Tá, mas e a velocidade do foguete?
Agora que relembramos o que significa uma integral e como calculá-la numericamente no MATLAB, vamos voltar pro exemplo do foguete. Como podemos calcular sua velocidade com o que vimos até aqui?
A velocidade de um foguete é calculada a partir da integração numérica da aceleração, que é medida por sensores que enviam um sinal a um acelerômetro. O acelerômetro integra o sinal de aceleração no tempo para estimar a velocidade do foguete e, em seguida, integra a velocidade para ter uma estimativa do deslocamento.
Digamos que a aceleração de um foguete, partindo do repouso, foi medida durante . As medições são apresentadas na tabela abaixo:

Como podemos estimar a velocidade deste foguete após ? Lembra que obtemos a velocidade quando integramos a aceleração no tempo? Observe que na tabela temos as medições de aceleração a cada instante. Logo, podemos usar a função do MATLAB, com as seguintes linhas de código:

Na primeira linha, criamos um vetor que armazena a primeira linha da tabela, isto é, o instante de tempo de cada medição. Na segunda linha, criamos um vetor que contém os valores de aceleração da tabela.
Usamos os vetores e como entrada da função para encontrar a velocidade do foguete após . retorna a variável , que contém o resultado da integração numérica do vetor em relação ao vetor . Esta variável representa a velocidade do foguete após , que equivale a :
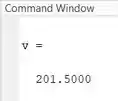
Uma característica que vale destacar da função é que, caso eu não entre com o vetor representando o intervalo de integração, o MATLAB considera um espaçamento unitário. Vai ficar mais fácil de entender se voltarmos ao exemplo do foguete.
Suponha que eu não defina o vetor no programa e entre somente com o vetor :
![]()
Como está sozinho na entrada da função e possui elementos, o MATLAB vai fazer a integração numérica considerando o intervalo de integração de a , indo de em . Na prática, o MATLAB vai fazer os cálculos da mesma forma do código anterior, quando um vetor foi definido de acordo com a tabela. Vamos ver como fica o resultado?

Viu que deu na mesma? Isto aconteceu porque a medição de aceleração foi feita de em segundo.
E aí, curtiu a aula de hoje? Sentiu um pouco o gostinho de trabalhar com foguetes da NASA?
Lembra de fazer os exercícios para fixar o conteúdo, este pode ser mesmo um pequeno passinho para trabalhar como engenheiro da NASA =)
Tá, mas e a velocidade do foguete?
Exercícios Resolvidos
Exercício Resolvido #1
“Unicamp – Adaptado de Exercícios de Cálculo Numérico da disciplina MS211 - Cálculo Numérico, exercício 20.3”
Seja
Estime pela regra dos trapézios utilizando apenas os valores tabelados abaixo:

Passo 1
O exercício pede para resolvermos a integral com os valores da tabela, usando a regra dos trapézios.
Podemos fazer isso no MATLAB, usando a função , que permite calcular a integral numérica a partir de dados tabelados. A função terá como entrada a primeira linha da tabela, representando o intervalo de integração, e a segunda linha da tabela, representando .
Passo 2
O primeiro passo para resolvermos o exercício é entrarmos no MATLAB as informações dadas no enunciado. Crie um script novo no MATLAB e digite as duas linhas de código:
![]()
Na primeira linha de código, é criado um vetor que vai de a , com um passo de . Ele contém os valores da primeira linha da tabela e representa o intervalo de integração.
Na segunda linha de código, o vetor armazena os dados de apresentados na tabela.
Após criarmos esses dois vetores, temos tudo o que precisamos para usar a função .
Passo 3
A função do MATLAB tem a seguinte estrutura:
Ela nos retorna o resultado da integração, que representa a área sob a curva , definida no intervalo .
Neste exercício, o vetor entra no lugar de , pois representa o intervalo de integração, e o vetor entra no lugar de , já que representa para cada elemento do vetor .
Inclua no seu código o comando:
![]()
O comando vai calcular a integral e armazenar o resultado na variável .
Ao rodarmos o programa, temos como resultado:
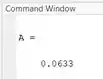
Resposta
A estimativa de pela regra dos trapézios utilizando apenas os valores tabelados é de .
Exercício Resolvido #2
“(UFScar) Cálculo Numérico: Uma Abordagem para o Ensino a Distância, de Selma Helena de Vasconcelos Arenales e José Antonio Salvador. São Carlos : EdUFSCar, 2010. p. 133 (Coleção UAB-UFSCar)”
Com o software MATLAB, usando a Regra dos Trapézios, calcule as integrais das seguintes funções:
Passo 1
O exercício pede para usarmos o MATLAB para calcular a integral numérica de duas funções, usando a Regra dos Trapézios. Isto quer dizer que nos é pedido para usar a função do MATLAB, que calcula integrais usando o método dos trapézios.
Passo 2
A letra pede para calcular a integral da função:
Crie um script novo no MATLAB e entre com as duas linhas de código:
![]()
Na primeira linha de código, foi criado um vetor , que vai de a com um passo de . Este vetor representa o intervalo de no qual vamos integrar a função. Escolhi um passo de para ter uma maior precisão no resultado, mas você pode escolher o passo que quiser. Mas lembre que quanto menor o passo, maior a precisão da integral numérica.
Na segunda linha de código, o comprimento de foi armazenado na variável .
Agora vamos calcular a função para cada elemento de . Para fazermos isso, teremos que criar um laço , como no código abaixo:

Primeiramente, é criado um vetor de zeros de mesmo comprimento de , por meio do comando . Este vetor é chamado de e cada elemento dele vai ser substituído no laço , sendo atualizado com o valor da função para cada valor de .
Em seguida, inicia-se o laço , criando-se uma variável de controle que vai de a . No bloco do , a função é calculada para cada elemento do vetor e o resultado é armazenado no elemento de mesma posição do vetor .
Com os vetores e definidos, já podemos calcular a integral da letra do exercício.
Passo 3
No passo anterior, foram criadas as duas entradas que precisamos para usar a função para calcular a integral da função. Lembrando que tem a seguinte estrutura:
Ela nos retorna o resultado da integração, que representa a área sob a curva , definida no intervalo .
Para a letra do exercício, inclua no seu script a seguinte linha de código:
![]()
A integral da letra é resolvida por meio desta linha de código, usando os vetores que criamos no passo 2. Ao rodarmos o programa, temos como resposta:

Lembre que se você usou um passo diferente de , seu resultado pode ser um pouquinho diferente, mas não significa que está errado. Você só dividiu a área sob a curva em partes de tamanho diferente do que eu fiz.
Pronto! Letra resolvida. Vamos fazer a letra .
Passo 4
A letra pede para calcular a integral da função:
Para resolvermos a letra , usaremos o mesmo passo a passo que fizemos para a letra . Em um novo script do MATLAB, digite as duas linhas de código:
![]()
De maneira similar ao passo 2, foi criado um vetor , que vai de a com um passo de , na primeira linha de código. Escolhi novamente um passo de , mas você pode usar o passo que quiser. Assim como no passo 2, este vetor representa o intervalo de no qual vamos integrar a função.
Na segunda linha de código, o comprimento de foi armazenado na variável .
Agora vamos calcular a função para cada elemento de . Novamente, vamos criar um laço :
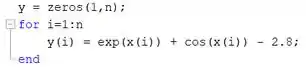
Este pedaço de código faz exatamente a mesma coisa que o pedaço de código com o laço apresentado no passo 2.
Primeiramente, é criado um vetor de zeros de mesmo comprimento de . Cada elemento de vai ser atualizado no laço com o valor da função para cada elemento de .
Em seguida, inicia-se o laço , criando-se uma variável de controle que vai de a . No bloco do , a função é calculada para cada elemento do vetor e o resultado é armazenado no elemento de mesma posição do vetor .
Executando este passo, já temos tudo o que precisamos para calcular a integral da letra do exercício.
Passo 5
Vamos usar a função para calcular a integral da letra . Inclua no seu código o comando:
![]()
Este comando vai retornar a integral da função , representada pelo vetor , para o intervalo representado pelo vetor . O resultado é armazenado na variável , que, aós rodar o código, equivale a:

Lembre que seu resultado pode ser um pouquinho diferente do meu, caso você tenha usado um passo diferente na criação do vetor .
Letra resolvida!
Resposta
Exercício Resolvido #3
“Adaptado de Numerical Methods in Engineering with Matlab, de Jaan Kiusalaas (Pennsylvania State University), exercício 2, p. 214”
A tabela abaixo mostra a potência fornecida às rodas motrizes de um carro em função da velocidade .

Se a massa do carro é de , determine o intervalo de tempo para que o carro acelere de para . Use o método dos trapézios para a integração. Dica:
que pode ser deduzido a partir da lei de Newton e a definição de potência .
Passo 1
O enunciado pede para resolvermos a integral:
Usando os dados de e da tabela. Como temos valores numéricos de e , isto significa que devemos usar integração numérica para resolvermos o problema (que foi o que o enunciado pediu, no final das contas). O resultado da integral corresponde ao intervalo de tempo que o carro de leva para acelerar de a .
Como o enunciado pediu para usarmos o método dos trapézios para calcular a integral, usaremos a função do MATLAB para resolver a questão.
Passo 2
O primeiro passo para resolver o problema é entrar com os dados do enunciado no MATLAB, para daí calcularmos a integral. Crie um script novo no MATLAB e digite as três linhas de código abaixo:

Na primeira linha, foi criada uma variável para armazenar a massa do carro, de .
Na segunda linha, foi criado um vetor para armazenar os valores de velocidade da primeira linha da tabela. Não entramos com (primeira coluna da tabela) pois queremos integrar de a .
Na terceira linha, foi criado um vetor para armazenar os valores de potência da segunda linha da tabela. Novamente, não entramos com a potência da primeira coluna da tabela, pois não faz parte do intervalo de integração.
Note que o vetor é multiplicado por . Isto foi feito para converter para , para obtermos em segundos. Se não fizermos esta conversão, será dado em milissegundos.
Passo 3
Depois de entrarmos as informações dadas no enunciado no nosso script do MATLAB, vamos criar um vetor representando a função de dentro da integral: . Para isto, inclua no seu código o comando:
![]()
Com este comando, dividimos cada elemento de pelo elemento de que esteja na mesma posição, o que resulta no vetor .
O vetor corresponde à função a ser integrada.
Passo 4
Após concluir o passo 3, temos todos os recursos para resolver a integral:
Usando a função do MATLAB. Lembrando que tem a seguinte estrutura:
Ela nos retorna o resultado da integração, que representa a área sob a curva , definida no intervalo .
Para nosso problema, o vetor entraria no lugar de e o vetor no lugar de . No seu programa, digite a linha de código:
![]()
Este comando resolve a integral:
Para encontrarmos , ainda temos que multiplicar o resultado da integral por :
![]()
O produto resulta no intervalo de tempo para o carro de acelerar de para . O intervalo de tempo é armazendo na variável .
Ao rodarmos o código, temos o seguinte resultado:

O valor de é a resposta do exercício.
Resposta
O carro de demora para acelerar de para .
Exercício Resolvido #4
“Adaptado de Numerical Methods in Engineering with Matlab, de Jaan Kiusalaas (Pennsylvania State University), exercício 13, p. 217”
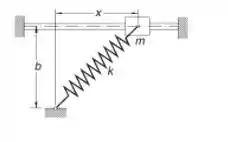
A massa é ligada a uma mola de comprimento livre e rigidez . O coeficiente de atrito entre a massa e a haste horizontal é . A aceleração da massa pode ser demonstrada como , onde
Se a massa é liberada a partir do repouso em , sua velocidade em é dada por
Calcule por meio de integração numérica usando como dados , , , e .
Passo 1
O exercício pede para calcularmos a velocidade resolvendo a equação:
Para encontrarmos antes temos que resolver a integral dentro da raiz, usando integração numérica. Para solucionar a integral, podemos usar a função do MATLAB.
O enunciado nos dá como dados:

Com os valores da tabela, podemos definir o intervalo de integração, que vai de a , e podemos calcular . Desta forma, temos as entradas de .
Passo 2
A primeira coisa que devemos fazer é entrar com os dados fornecidos pelo enunciado no MATLAB. Crie um novo script e digite as linhas de código:
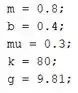
Com estes comandos, entramos no programa os dados da tabela apresentada no passo 1. Chamei a variável que armazena o coeficiente de atrito de , que é uma das formas de pronunciar , já que não podemos usar letras gregas como nome de variáveis no MATLAB.
Vamos agora criar o intervalo de integração. Ele será representado por um vetor , construído com o comando:
![]()
O vetor vai de a , com um passo de . Eu adotei o passo de para gerar um resultado mais preciso na integração mais pra frente, mas você pode adotar o passo que quiser. Só não se esqueça que o tamanho do passo tem impacto direto sobre a precisão da integração: quanto menor o passo, mais precisa é a integração numérica.
Após ter digitado o comando para criar , adicione logo abaixo a linha de código:
![]()
Esta linha vai armazenar a quantidade de elementos do vetor na variável , por meio da função , que retorna o comprimento de um vetor. Precisamos do número de elementos de para podermos calcular usando um laço .
Agora, vamos criar um vetor representando a função ser integrada:
Como dito, usaremos um laço para isto, por meio das linhas de código abaixo:

Primeiramente, é criado um vetor de zeros de mesmo comprimento de , por meio do comando . Este vetor é chamado de e cada elemento dele vai ser substituído no laço pelo resultado de para cada elemento do vetor .
Em seguida, inicia-se o laço , criando-se uma variável de controle que vai de a . No bloco do , a função é calculada para cada elemento do vetor e o resultado é armazenado no elemento de mesma posição do vetor .
Concluído este passo, temos tudo o que precisamos para fazer a integração.
Passo 3
Para resolvermos a integral, usaremos a função que tem o seguinte formato:
Ela nos retorna o resultado da integração, que representa a área sob a curva , definida no intervalo .
Para nosso problema, o vetor entraria no lugar de e o vetor no lugar de . No seu programa, digite a linha de código:
![]()
Este comando resolve a integral:
Para encontrarmos , ainda precisamos fazer algumas continhas com o resultado da integral, armazenado na variável , retornada por . Lembre que é dado por:
No seu script, digite logo abaixo de a linha de código:
![]()
Esta linha calcula usando a expressão dada no enunciado e armazena o resultado em .
Ao executarmos nosso programa, temos o seguinte resultado para :

Resposta
A velocidade da massa em é de .
Exercício Resolvido #5
“Adaptado de UERJ - Curso de MATLAB 5.1: Introdução à Solução de Problemas de Engenharia, Laboratório de Engenharia Elétrica, p. 123”
A análise do fluxo de um líquido em duto tem aplicação em muitos sistemas diferentes, incluindo o estudo em veias e artérias no corpo humano, o sistema hidráulico de uma cidade, o sistema de irrigação de uma fazenda, o sistema de jato de tinta de uma impressora, etc.
O atrito de um fluxo ao passar num oleoduto circular gera a chamada velocidade de perfil no fluido.
O óleo que está em contato com as paredes do duto não está se movendo na mesma velocidade que o óleo no centro do fluido. O diagrama abaixo mostra como a velocidade do óleo varia de acordo com o diâmetro do duto e define as variáveis usadas para esta análise:
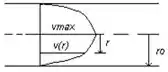
A velocidade de perfil é definida pela seguinte equação:
onde é um número inteiro entre 5 e 10 que define o contorno do escoamento do óleo. A velocidade média de escoamento do óleo pode ser calculada integrando-se a velocidade de perfil no intervalo de a :
Os valores de e de podem ser medidos experimentalmente, e o valor de é o próprio raio do tubo. Escreva um programa no MATLAB para integrar a velocidade de perfil e assim determinar a velocidade média do óleo no duto.
Conside , e .
Passo 1
O enunciado pede para encontrarmos a velocidade média de um óleo escoando em um duto de raio , com uma velocidade máxima de . Para isto, devemos resolver no MATLAB a seguinte integral:
onde
O resultado desta integral é a velocidade média do óleo. Devemos considerar .
Para calcularmos a integral do enunciado, podemos usar a função do MATLAB.
Passo 2
O primeiro passo é entrarmos com as informações do enunciado no MATLAB. Crie um script novo e digite as linhas de código:
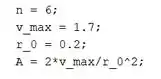
Criamos variáveis para armazenar os valores , e . Respectivamente, são as variáveis , e .
Em seguida, calculamos a constante , que é armazenada na variável .
O passo seguinte consiste em criar as entradas para a função .
Passo 3
Vamos criar o intervalo de integração com as seguintes linhas de código:
![]()
Na primeira linha, é criado um vetor que vai de a , com um passo de . O vetor representa o intervalo de integração pra encontrar a velocidade média do óleo no duto, lembrando que é o raio do duto.
Eu adotei o passo de para gerar um resultado mais preciso na integração mais pra frente, mas você pode adotar o passo que quiser. Só não se esqueça que o tamanho do passo tem impacto direto sobre a precisão da integração: quanto menor o passo, mais precisa é a integração numérica.
Na segunda linha de código, a função conta quantos elementos tem o vetor e armazena o resultado a variável .
Agora, vamos criar um vetor representando a função ser integrada: . Para isto, usaremos um laço , por meio das linhas de código abaixo:
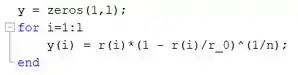
Primeiramente, é criado um vetor de zeros de mesmo comprimento de , por meio do comando . Este vetor é chamado de e cada elemento dele vai ser substituído no laço pelo resultado de para cada elemento do vetor .
Em seguida, inicia-se o laço , criando-se uma variável de controle que vai de a . No bloco do , a função é calculada para cada elemento do vetor e o resultado é armazenado no elemento de mesma posição do vetor .
Concluído este passo, temos tudo o que precisamos para fazer a integração pedida no enunciado.
Passo 4
Para resolvermos a integral, usaremos a função que tem o seguinte formato:
Ela nos retorna o resultado da integração, que representa a área sob a curva , definida no intervalo .
Para nosso problema, o vetor entraria no lugar de e o vetor no lugar de . No seu programa, digite a linha de código:
![]()
Este comando resolve a integral:
Para encontrarmos a velocidade média , temos que multiplicar o resultado da integral pela constante , que definimos lá no passo 2:
![]()
O produto corresponde à velocidade média do óleo escoando no duto, a qual é armazenada na variável .
Ao rodarmos o script do MATLAB, chegamos ao seguinte resultado:

O valor de é a resposta do exercício.
Resposta
A velocidade média do fluxo de óleo escoando por um duto de raio , com uma velocidade máxima de e considerando é de .
Exercício Resolvido #6
“Adaptado de Numerical Methods in Engineering with Matlab, de Jaan Kiusalaas (Pennsylvania State University), exercício 12, p. 216”

A figura mostra um semi-espaço elástico que carrega um carregamento uniforme de intensidade sobre uma área circular de raio . O deslocamento vertical da superfície no ponto pode ser calculado como

onde é o deslocamento em . Use integração numérica para determinar em .
Passo 1
O exercício pede para calcularmos a razão usando integração numérica. Para determinar , basta resolver a integral, pois:
Para resolver a integral de forma numérica, podemos usar a função do MATLAB, que calcula integrais usando o método dos trapézios.
Passo 2
Em um novo script, crie o intervalo de integração com a linha de código:
![]()
Esta linha cria um vetor , que vai de a com um passo de , representando o intervalo de no qual vamos integrar a função. Escolhi um passo de para ter uma maior precisão no resultado, mas você pode escolher o passo que quiser. Mas lembre que quanto menor o passo, maior a precisão da integral numérica.
Passo 3
Em seguida, vamos calcular a função dentro da integral para cada valor do vetor . Podemos simplificar a função ao adotar :
Em seu script, implemente o cálculo de para cada valor de contido no vetor com a linha de código:
![]()
Os valores de para cada elemento de são armazenados no vetor .
Note o uso dos operadores e : eles indicam ao MATLAB que cada elemento de um vetor deve ser elevado ao quadrado e dividido pelo elemento de mesma posição no vetor do denomindor de uma divisão, respectivamente.
Passo 4
Nos dois passos anteriores, foram criadas as duas entradas que precisamos para usar a função para calcular a integral e obter : os vetores e . Lembrando que tem a sintaxe:
Ela nos retorna o resultado da integração, que representa a área sob a curva , definida no intervalo .
Inclua no seu script a seguinte linha de código:
![]()
Este comando resolve numericamente a integral e armazena em o resultado dela, que é a razão . Ao rodar o programa, vemos que é igual a:
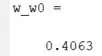
Resposta
Exercício Resolvido #7
“Adaptado de Numerical Methods in Engineering with Matlab, de Jaan Kiusalaas (Pennsylvania State University), exercício 5, p. 215”

A tabela abaixo fornece a força do arco em função da distância . Se o arco for puxado , determine a velocidade da flecha de quando ela deixa o arco.

Dica: a energia cinética da flecha é igual ao trabalho realizado ao puxar o arco, isto é:
Passo 1
O exercício pede para encontrarmos a velocidade da flecha resolvendo a integral:
Usando os dados de e da tabela. Como temos valores numéricos de e , isto significa que devemos usar integração numérica para resolvermos o problema. Para isto, usaremos a função do MATLAB. Com a solução da integral, conseguimos encontrar ao isolá-lo na equação acima.
Passo 2
O primeiro passo para resolver o problema é entrar com os dados das tabelas no MATLAB, para daí calcularmos a integral. Crie um script novo no MATLAB e digite as linhas de código abaixo:
![]()
Na primeira linha, foi criado um vetor para armazenar os valores de da tabela. Como aumenta a um passo constante na tabela, o vetor foi criado usando a sintaxe de forma que ele vai de a , com um passo de .
Na segunda linha, foi criado um vetor para armazenar os valores de força da tabela.
Passo 3
Já temos todos os recursos para resolver a integral:
Usando a função do MATLAB. Lembrando que tem a sintaxe:
Ela nos retorna o resultado da integração, que representa a área sob a curva , definida no intervalo .
Para nosso problema, o vetor entraria no lugar de e o vetor no lugar de . No seu programa, digite a linha de código:
![]()
O resultado da integral é armazenado em .
Passo 4
Para encontrar , devemos isolá-lo na equação:
Temos que é igual a:
Por isso, em seu programa, entre com a massa da flecha e implemente a equação acima, por meio das duas linhas de código:
![]()
Ao executar o programa, temos , a velocidade da flecha quando ela deixa o arco:

Resposta
Exercício Resolvido #8
“Adaptado de Numerical Methods in Engineering with Matlab, de Jaan Kiusalaas (Pennsylvania State University), exercício 14, p. 217”
A fórmula de Debye para a capacidade calorífica de um sólido é , onde
![]()
Os termos desta equação são
- número de párticulas no sólido
- constante de Boltzmann
- temperatura absoluta
- temperatura de Debye
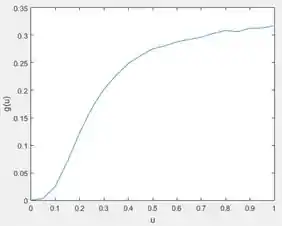
Calcule de a em intervalos de e plote os resultados.
Passo 1
O exercício pede para calcularmos para diferentes valores de . Isto faz com que tenhamos que resolver a integral
várias vezes, para diferentes intervalos de integração, visto que define tal intervalo.
Por isso, usaremos a função dentro de um laço , para que a integral seja resolvida para cada valor de . A função também será calculada dentro do mesmo laço .
Ao final, plotaremos a curva de em função de com o comando .
Passo 2
Vamos começar definindo o intervalo de com o qual se deseja calcular . Em um script novo, digite o comando:
![]()
Este comando cria um vetor contendo os valores de com quais calcularemos . O enunciado pediu para fazermos indo de a , com um passo de . Por isso, o vetor vai de a , com um passo de .
Antes de iniciar o laço , vamos criar um vetor para armazenar o resultado de para cada valor de . Para isso, digite em seu script as linhas de código:
![]()
Na primeira linha, armazenamos na variável o número de elementos do vetor , por meio da função , que nos dá a quantidade de elementos de um vetor.
Na segunda linha, criamos um vetor composto só de zeros, com a mesma quantidade de elementos do vetor , por meio da função .
O vetor receberá o resultado de para cada valor de , tendo seus elementos atualizados dentro do laço .
Passo 3
Comece a implementar o laço , usando uma variável de controle que vai de 1 a .

Variando de a , conseguiremos acessar um a um todos os elementos do vetor por meio do laço . Também conseguiremos ir preenchendo o vetor , ao calcular dentro do laço e armazenando o resultado no elemento correspondente de .
Note que o intervalo de integração vai de a e o primeiro valor de é , o que dará um erro de divisão por . Por isso, precisamos incluir dentro do nosso uma condição para dizer ao MATLAB o que fazer quando . Quando , , por isso, inclua dentro do os comandos:

Desta forma, dizemos que se o elemento do vetor for igual a , o elemento do vetor também será igual a .
Caso seja diferente de , não haverá erro de divisão por no intervalo de integração. Por isso, é dentro do que faremos o cálculo da integral.
Passo 4
Para calcular a integral , precisamos definir o intervalo de integração, calcular para cada valor do intervalo e usar a função para calcular a integral. Lembrando que tem a sintaxe:
Ela nos retorna o resultado da integração, que representa a área sob a curva , definida no intervalo .
Por isso, após o dentro laço , digite as quatro linhas de código:

A linha
![]()
Cria um vetor , que vai de a , onde é o valor de na iteração , com um passo de . O vetor representa o intervalo de no qual vamos integrar a função. Escolhi um passo de para ter uma maior precisão no resultado, mas você pode escolher o passo que quiser. Mas lembre que quanto menor o passo, maior a precisão da integral numérica.
Na linha
![]()
Calculamos para cada elemento do vetor . Note os comandos , e , indicando que as operações são realizadas por elemento do vetor .
Na linha
![]()
Calculamos a integral. Contudo, perceba que eu não usei simplesmente e como entrada, mas sim e . Isto é, usei como entrada os dois vetores começando no seu segundo elemento. Fiz isso para não pegar o valor , pois , logo, o primeiro elemento de corresponde a (“not a number”, no MATLAB), o que não permite calcular a integral com .
Finalmente, na linha
![]()
Calculamos , multiplicando o resultado da integração pelo valor de da iteração elevalo ao cubo. O resultado é armazenado no elemento do vetor .
Desta forma, o laço está completo.
Passo 5
Para finalizar, vamos plotar o gráfico de em função de . Para isto, adicione as linhas de código:

Com a primeira linha, plotamos o gráfico do vetor em função do vetor .
Na segunda linha, dizemos que o eixo horizontal do gráfico corresponde a . Já na terceira linha, dizemos que o eixo vertical corresponde a .
Execute o programa e você terá o gráfico pedido pelo exercício.
Resposta