Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Lugar das Raízes

Ver Todos os Exercícios

Teoria

Introdução

E aí, controleiro de plantão, tudo joia? Já ouviu falar de lugar das raízes?

“Sim! As raízes das plantas ficam debaixo da terra!”

Não, jovem gafanhoto, estou falando de outro tipo de raiz. Se você já assistiu alguma disciplina de Controle na sua graduação, você provavelmente aprendeu como esboçar o “lugar geométrico das raízes” a partir de alguma função de transferência. Na aula de hoje, vamos aprender como se faz isso no MATLAB.

Se você não lembra, não se preocupe, vamos dar uma revisada nos conceitos principais. E caso você queira se aprofundar mais ou precise dar uma reforçada no conteúdo, aqui no Responde Aí temos um capítulo só sobre lugar das raízes para você dar uma olhada ;D

Em controle, usamos o lugar das raízes para encontrar quais valores um ganho K pode assumir no meu controlador para que meu sistema continue estável.

Vamos de exemplo. Digamos que estamos projetando uma malha de controle representada pelo diagrama de blocos abaixo:

Queremos saber quais valores o ganho K pode assumir de forma que a malha permaneça estável.

Para determinar o lugar das raízes, usamos a função de transferência de malha aberta, deixando o K de lado, que vou chamar de G ( s ) :

G s = s + 2 s 3 + 4 s 2 + 3 s = s + 2 s ( s + 3 ) ( s + 1 )

Chamamos de zeros as raízes do polinômio do numerador da função de transferência. No caso de G ( s ) , temos apenas um zero, que é z 1 = - 2 .

Já as raízes do denominador da função de transferência são os polos. Em G ( s ) , temos três polos: p 1 = 0 , p 2 = - 3 e p 3 = - 1 .

O lugar das raízes é esboçado em um plano complexo, onde o eixo horizontal representa a parte real das raízes e o eixo vertical, a parte imaginária. A figura abaixo apresenta o lugar das raízes de G ( s ) :

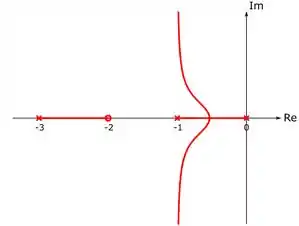
Na figura, o zero é representado por uma bolinha e os polos, por xisinhos. As linhas em vermelho são chamadas de ramos e representam os valores que as raízes assumem ao variarmos K de 0 a ∞ . Os ramos começam nos polos (onde temos K = 0 ) e terminam nos zeros (onde K = ∞ ).

Uma malha de controle é estável se as raízes forem números reais negativos ou se forem números complexos com a parte real negativa. No lugar das raízes, isso significa que as raízes devem estar à esquerda do eixo vertical. Este é o caso do nosso exemplo G ( s ) : repare que o zero, os polos e as linhas em vermelho estão todos à esquerda do eixo Im. Isso significa que K pode assumir qualquer valor entre 0 e ∞ que a malha continuará estável.

Depois dessa revisadinha básica sobre lugar das raízes, vamos aprender a esboçá-lo no MATLAB e como descobrir quais valores K pode assumir.

Traçando o lugar das raízes no MATLAB

Para traçarmos o lugar das raízes no MATLAB, usamos o comando:

r l o c u s ( f u n c a o   d e   t r a n s f e r e n c i a )

A função r l o c u s tem como entrada uma função de transferência criada a partir do comando t f . Ao executarmos o programa, r l o c u s gera um gráfico com o lugar das raízes.

Para vermos direitinho como o r l o c u s funciona, vamos aplicá-lo no nosso exemplo. Crie um novo script no MATLAB e adicione os comandos abaixo para criar a função de transferência G s = s + 2 s 3 + 4 s 2 + 3 s :

Na primeira linha, criamos um vetor chamado n u m com os coeficientes do polinômio do numerador de G ( s ) .

Na segunda linha, criamos um vetor chamado d e n com os coeficientes do polinômio do denominador de G ( s ) .

Na terceira linha, criamos G ( s ) usando a função t f do MATLAB, armazenando G ( s ) na variável s i s .

Para gerar o lugar das raízes de G ( s ) , digite o comando:

Ao rodar seu script, aparecerá o gráfico do lugar das raízes:

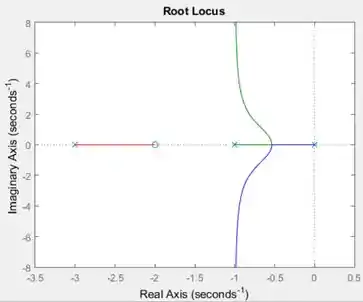
Como na figura da introdução, a bolinha representa os zeros e os xisinhos, os polos. No MATLAB, cada ramo é traçado com uma cor diferente.

Podemos ver o valor de K clicando sobre os ramos. Aparecerá um quadradinho preto com uma janelinha apresentando algumas propriedades da função de transferência naquele ponto:

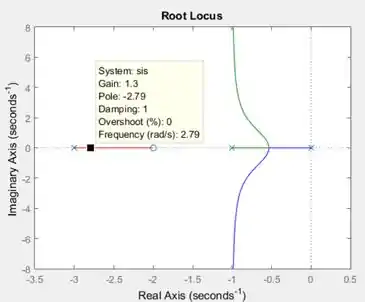
O ganho K é dado pelo valor ao lado de G a i n na janelinha. Por exemplo, onde cliquei, K = 1,3 . A janelinha apresenta ainda outras propriedades que estudamos normalmente na disciplina de Controle, mas não precisamos entrar em detalhes aqui.

Posso arrastar o quadradinho preto em direção ao polo, onde terei K = 0 :

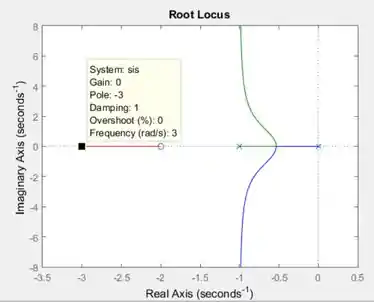
E também posso arrastar em direção ao zero, onde terei K = ∞ :

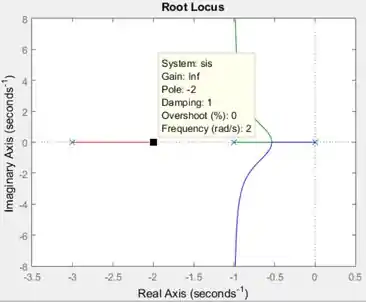
No nosso exemplo, vimos que, como o lugar das raízes se encontra todo à esquerda do eixo vertical do gráfico, as raízes sempre terão parte real negativa, não importa o valor do ganho K . Por isso, K pode assumir qualquer valor entre 0 e ∞ .

Contudo, existem casos em que parte do lugar das raízes estará à direita do eixo vertical, indicando que existem ganhos que fazem com que as raízes tenham parte real positiva, tornando a malha instável. A funcionalidade do MATLAB de arrastar o quadradinho preto para vermos os valores do ganho no lugar das raízes, isto é, os valores de K , ajuda a determinar a faixa de valores que K pode assumir de forma a manter a estabilidade.

Por exemplo, este é o lugar das raízes para a função de transferência H ( s ) = ( 2 s + 1 ) / ( s 3 + s 2 + 3 s + 10 ) :

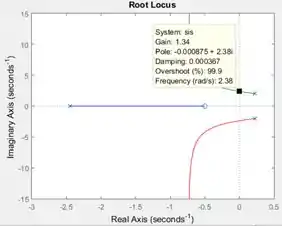
Se encaixa bem na situação descrita acima, né? Arrastando o quadradinho preto, vemos que K   tem que ser no mínimo 1,34 . Se K for menor que isso (arrastando o quadradinho preto mais para a direita, em direção ao xis), a parte real das raízes torna-se positiva e a malha, instável.

E aí? Curtiu a aula? Agora é fazer alguns exercícios para praticar e se tornar um controleiro nota 10 ;D

Traçando o lugar das raízes no MATLAB

Exercícios Resolvidos

Exercício Resolvido #1

“Adaptado de Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, p. 254, problema 8-1b.”

Esboce o lugar geométrico das raízes para o sistema mostrado abaixo:

G s = 3 s + 1 2 s + 1

Passo 1

O exercício pede para traçar o lugar das raízes de G ( s ) . Para fazermos o que o exercício pede, usaremos duas funções do MATLAB. Primeiro, vamos usar a função t f para entrar com G ( s ) . Em seguida, usaremos r l o c u s para plotar o lugar das raízes de G ( s ) .

Passo 2

O primeiro passo para resolver o exercício é entrar com G ( s ) no MATLAB. Para isto, usaremos a função t f , que cria funções de transferência e tem a seguinte sintaxe:

s i s t e m a = t f ( n u m e r a d o r , d e n o m i n a d o r )

A função t f tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por n u m e r a d o r ) e outro contendo os coeficientes do polinômio do denominador (representado por d e n o m i n a d o r ). t f retorna um objeto representando a função de transferência, que será armazenada em s i s t e m a .

Para G ( s ) , o polinômio do numerador é 3 s + 1 . Já o polinômio do denominador é 2 s + 1 .

Abra um script novo no MATLAB e crie dois vetores, um contendo os coeficientes de 3 s + 1 e outro contendo os coeficientes de 2 s + 1 , indo do elemento com maior expoente ao de menor expoente:

O vetor n u m contém os coeficientes do numerador e o vetor d e n , do denominador de G ( s ) .

Em seguida, adicione o comando abaixo para criar G ( s ) :

A função de transferência é armazenada na variável G . Você pode ver como G   ficou ao rodar o programa e pedir ao MATLAB para imprimir G no Command Window:

Passo 3

Após criar G ( s ) , usaremos a função r l o c u s para plotar o lugar das raízes. r l o c u s tem a sintaxe:

r l o c u s ( f u n ç ã o   d e   t r a n s f e r ê n c i a )

A função r l o c u s tem como entrada uma função de transferência criada a partir do comando t f (no nosso caso, é a variável G ). Ao executarmos o programa, r l o c u s gera um gráfico com o lugar das raízes da função de trasnferência.

Adicione no seu script o comando:

Ao executar o programa, você terá o gráfico do lugar das raízes de G ( s ) .

Resposta

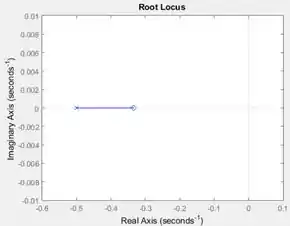
Exercício Resolvido #2

“Adaptado de Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, p. 254, exemplo 8-2.1.”

Esboce o lugar geométrico das raízes para o sistema mostrado abaixo:

G s = 1 3 s 2 +   4 s   +   1

Passo 1

O exercício pede para traçar o lugar das raízes de G ( s ) . Para fazermos o que o exercício pede, usaremos duas funções do MATLAB. Primeiro, vamos usar a função t f para entrar com G ( s ) . Em seguida, usaremos r l o c u s para plotar o lugar das raízes de G ( s ) .

Passo 2

Para entrarmos com G ( s ) no MATLAB, usaremos a função t f , que tem como sintaxe:

s i s t e m a = t f ( n u m e r a d o r , d e n o m i n a d o r )

A função t f tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por n u m e r a d o r ) e outro contendo os coeficientes do polinômio do denominador (representado por d e n o m i n a d o r ). t f retorna um objeto representando a função de transferência, que será armazenada em s i s t e m a .

Para G ( s ) , o polinômio do numerador é 1 . Já o polinômio do denominador é 3 s 2 + 4 s + 1 .

Em um novo script, vamos criar duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para t f . Como o polinômio do numerador tem somente um elemento correspondendo a 1 ∙ s 0 = 1 ∙ 1 = 1 , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de n u m e ela é igual a 1 .

A outra variável é um vetor chamado d e n , contendo os coeficientes de 3 s 2 + 4 s + 1 , indo do elemento com maior expoente ao de menor expoente:

Em seguida, adicione o comando abaixo para criar G ( s ) :

A função de transferência é armazenada na variável G . Você pode ver como G   ficou ao rodar o programa e pedir ao MATLAB para imprimir G no Command Window:

Passo 3

Após criar G ( s ) , usaremos a função r l o c u s para plotar o lugar das raízes. r l o c u s tem a sintaxe:

r l o c u s ( f u n ç ã o   d e   t r a n s f e r ê n c i a )

A função r l o c u s tem como entrada uma função de transferência criada a partir do comando t f (no nosso caso, é a variável G ). Ao executarmos o programa, r l o c u s gera um gráfico com o lugar das raízes da função de trasnferência.

Adicione no seu script o comando:

Ao executar o programa, você terá o gráfico do lugar das raízes de G ( s ) .

Resposta

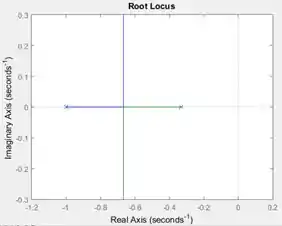
Exercício Resolvido #3

“Adaptado de UnB – 107506: Laboratório de Controle de Processos. Aula: MATLAB. Prof. Eduardo Stockler Tognetti (2018) – Exercício 4”

Seja

F ( s ) = 5 s 2 + 3 s + 6 s 4 + 3 s 3 + 7 s 2 + 9 s + 12

Plote o lugar das raízes e ache os polos e os zeros de F ( s ) .

Passo 1

O exercício pede para plotar o lugar das raízes de F ( s ) e, a partir do gráfico do lugar das raízes, identificar os polos e os zeros da função de transferência. Lembrando que os zeros são as raízes do numerador de F ( s ) , isto é, de 5 s 2 + 3 s + 6 . Como se trata de um polinômio de 2 º grau, temos que identificar dois zeros no lugar das raízes.

Já os polos são as raízes do denominador de F ( s ) , isto é, de s 4 + 3 s 3 + 7 s 2 + 9 s + 12 . Como se trata de um polinômio do 4 º grau, existem quatro polos no lugar das raízes.

Para plotarmos o lugar das raízes, usaremos duas funções do MATLAB. Primeiro, vamos usar a função t f para entrar com F ( s ) no MATLAB. Em seguida, usaremos r l o c u s para plotar o lugar das raízes de F ( s ) .

Passo 2

O primeiro passo para resolver o exercício é entrar com F ( s ) no MATLAB. Para isto, usaremos a função t f , que cria funções de transferência e tem a seguinte sintaxe:

s i s t e m a = t f ( n u m e r a d o r , d e n o m i n a d o r )

A função t f tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por n u m e r a d o r ) e outro contendo os coeficientes do polinômio do denominador (representado por d e n o m i n a d o r ). t f retorna um objeto representando a função de transferência, que será armazenada em s i s t e m a .

Para F ( s ) , o polinômio do numerador é 5 s 2 + 3 s + 6 . Já o polinômio do denominador é s 4 + 3 s 3 + 7 s 2 + 9 s + 12 .

Em um novo script do MATLAB, crie dois vetores, um chamado de n u m que contém os coeficientes de 5 s 2 + 3 s + 6 e outro chamado d e n , contendo os coeficientes de s 4 + 3 s 3 + 7 s 2 + 9 s + 12 . Ambos os vetores vão do coeficiente do elemento com maior expoente ao coeficiente de menor expoente:

Em seguida, adicione o comando abaixo para criar F ( s ) :

A função de transferência é armazenada na variável F , isto é, F é igual a F ( s ) . Você pode confirmar isso rodando o programa e pedindo ao MATLAB para imprimir F no Command Window:

Passo 3

Após criar F ( s ) , usaremos a função r l o c u s para plotar o lugar das raízes. r l o c u s tem a sintaxe:

r l o c u s ( f u n ç ã o   d e   t r a n s f e r ê n c i a )

A função r l o c u s tem como entrada uma função de transferência criada a partir do comando t f (no nosso caso, é a variável F ). Ao executarmos o programa, r l o c u s gera um gráfico com o lugar das raízes da função de trasnferência.

Adicione no seu script o comando:

Ao executar o programa, você terá o gráfico do lugar das raízes de F ( s ) :

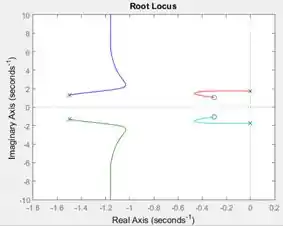
Passo 4

Podemos identificar os zeros e os polos no gráfico do lugar das raízes. Os zeros são representados por bolinhas e os polos, por xizinhos. Para sabermos quanto os zeros e os polos valem, podemos clicar sobre os ramos do gráfico. Aparecerá um quadradinho preto com um quadro com dados sobre o ponto onde você clicou. Esse quadradinho pode ser arrastado ao longo dos ramos até atingir um polo ou um zero.

Vamos começar com os zeros, que vou chamar de z 1 e z 2 . Repare que o gráfico tem duas bolinhas: isso porque o numerador é um polinômio de 2 º grau, logo, ele possui duas raízes. Vamos clicar nos ramos vermelho e azul piscina para aparecer o quadradinho preto e vamos arrastá-lo até as bolinhas:

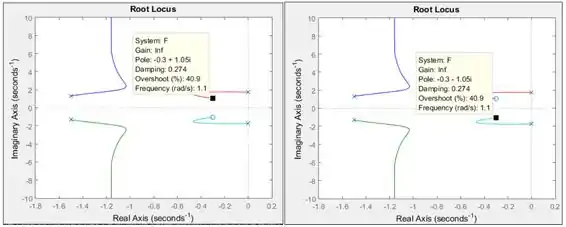
Você terá certeza que chegou no zero quando o dado G a i n for igual a I n f . Temos que os zeros de F ( s ) são:

z 1 = - 0,3 + 1,05 i

z 2 = - 0,3 - 1,05 i

Vamos agora identificar os polos. Temos quatro xizinhos no gráfico, representando os quatro polos de F ( s ) , que vou chamar de p 1 , p 2 , p 3 e p 4 . Existem quatro polos pois o denominador de F ( s ) é um polinômio de 4 º grau, isto é, ele possui quatro raízes. Clique nos quatro ramos para aparecer o quadradinho preto e arraste-o até cada um dos xizinhos:

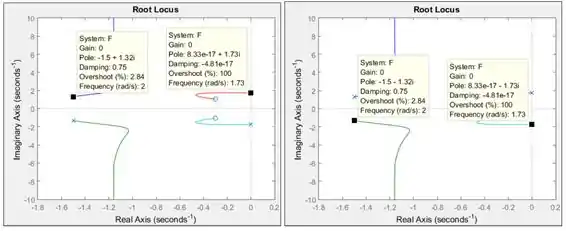
Você terá certeza que chegou no polo quando o dado G a i n for igual a 0 . Temos que os polos de F ( s ) são:

p 1 = - 1 , 5 + 1 , 32 i

p 2 = - 1,5 - 1,32 i

Os polos p 3 e p 4 estão sobre o eixo vertical, logo, eles são números puramente complexos, com parte real igual a 0 . Pelo que está indicado na figura acima, eles têm um resíduo na parte real de 8,33 ∙ 10 - 17 . É um número tão pequenininho, que podemos considerar igual a 0 . Logo, os outros dois polos de F ( s ) são:

p 3 = 1 , 73 i

p 4 = - 1,73 i

Resposta

Os zeros de F ( s ) são: z 1 = - 0,3 + 1,05 i e z 2 = - 0,3 - 1,05 i

Os polos de F ( s ) são:

p 1 = - 1,5 + 1,32 i

p 2 = - 1,5 - 1,32 i

p 3 = 1,73 i

p 4 = - 1,73 i

Exercício Resolvido #4

“Adaptado de Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 8.3”

Esboce o lugar geométrico das raízes para o sistema mostrado abaixo:

G s = 1 ( s + 2 ) ( s + 4 ) ( s + 6 )

Passo 1

O exercício pede para traçar o lugar das raízes de G ( s ) . Para fazermos o que o exercício pede, usaremos duas funções do MATLAB. Primeiro, vamos usar a função t f para entrar com G ( s ) . Em seguida, usaremos r l o c u s para plotar o lugar das raízes de G ( s ) .

Lembra da função t f ? Ela tem como entrada dois vetores com os coeficientes dos polinômios do numerador e do denominador da função de transferência. Repare que o denominador de G ( s ) está fatorizado. Logo, para podermos pegar os coeficientes dele, precisamos expandi-lo (isto é, multiplicar os termos) para gerarmos o polinômio. Por isso, antes de usarmos t f , faremos uma manipulação algébrica com o denominador de G ( s ) .

Passo 2

Primeiramente, vamos obter o polinômio do denominador de G ( s ) , multiplicando seus termos. Vamos fazer isso no MATLAB mesmo. Em um novo script, digite as linhas de código:

Na primeira linha, criamos uma variável simbólica s .

Na segunda linha, entramos com o denominador de G ( s ) , armazenando-o na variável d e n _ o r i g i n a l .

Na terceira linha, usamos o comando e x p a n d do MATLAB em d e n _ o r i g i n a l . Este comando multiplicará os termos de d e n _ o r i g i n a l e gerará o polinômio que precisamos, armazenando-o em d e n _ p o l .

Rodando o programa, temos:

Passo 3

Agora que temos o polinômio do denominador de G ( s ) , podemos criar os vetores que servirão de entrada para t f . Lembrando que t f que tem como sintaxe:

s i s t e m a = t f ( n u m e r a d o r , d e n o m i n a d o r )

A função t f tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por n u m e r a d o r ) e outro contendo os coeficientes do polinômio do denominador (representado por d e n o m i n a d o r ). t f retorna um objeto representando a função de transferência, que será armazenada em s i s t e m a .

Para G ( s ) , o polinômio do numerador é 1 . Já o polinômio do denominador é s 3 +   12 s 2 + 44 s + 48 .

Em um novo script ou no mesmo script onde você obteve d e n _ p o l , crie duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para t f . Como o polinômio do numerador tem somente um elemento correspondendo a 1 ∙ s 0 = 1 ∙ 1 = 1 , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de n u m e ela é igual a 1 .

A outra variável é um vetor chamado d e n , contendo os coeficientes de s 3 +   12 s 2 + 44 s + 48 , indo do elemento com maior expoente ao de menor expoente:

Em seguida, adicione o comando abaixo para criar G ( s ) :

A função de transferência é armazenada na variável G . Você pode ver como G   ficou ao rodar o programa e pedir ao MATLAB para imprimir G no Command Window:

Passo 4

Após criar G ( s ) , usaremos a função r l o c u s para plotar o lugar das raízes. r l o c u s tem a sintaxe:

r l o c u s ( f u n ç ã o   d e   t r a n s f e r ê n c i a )

A função r l o c u s tem como entrada uma função de transferência criada a partir do comando t f (no nosso caso, é a variável G ). Ao executarmos o programa, r l o c u s gera um gráfico com o lugar das raízes da função de trasnferência.

Adicione no seu script o comando:

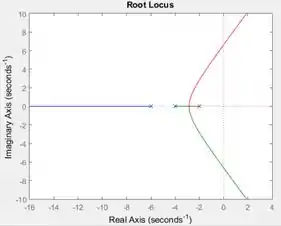
Ao executar o programa, você terá o gráfico do lugar das raízes de G ( s ) .

Resposta

Exercício Resolvido #5

“Adaptado de Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, p. 254, problema 6-10.”

Um processo pode ser definido pela seguinte função de transferência:

G s = 1 ( 5 s - 1 ) ( τ V s + 1 ) ( τ T s + 1 )

Onde τ V e τ T são as constantes de tempo da válvula de controle e do transmissor, respectivamente. Encontre a faixa de ganho da malha K para a qual a malha é estável se τ V = 0,1   m i n e τ T = 1   m i n .

Passo 1

O enunciado nos dá uma função de transferência G ( s ) e nos pede para determinar a faixa de valores que o ganho K de um controlador proporcional pode assumir, de forma que a malha seja estável.

Para determinarmos os valores de K , plotaremos o lugar das raízes de G ( s ) no MATLAB, usando a função r l o c u s , e acharemos os valores de K no próprio gráfico.

Antes disso, entraremos com G ( s ) no MATLAB, por meio da função t f .

Passo 2

Antes de tudo, vamos informar ao MATLAB as constantes de tempo das válvulas: τ V = 0,1   m i n e τ T = 1   m i n . Abra um script novo e digite:

A variável t _ V armazena τ V = 0,1   m i n e a variável t _ T , τ T = 1   m i n .

Agora, vamos entrar com a função de transferência G ( s ) , usando t f , que tem a sintaxe:

s i s t e m a = t f ( n u m e r a d o r , d e n o m i n a d o r )

A função t f tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por n u m e r a d o r ) e outro contendo os coeficientes do polinômio do denominador (representado por d e n o m i n a d o r ). t f retorna um objeto representando a função de transferência, que será armazenada em s i s t e m a .

Contudo, repare que o denominador de G ( s ) está fatorizado. Logo, para podermos pegar os coeficientes dele, precisamos expandi-lo (isto é, multiplicar os termos) para gerarmos o polinômio. Por isso, antes de usarmos t f , faremos uma manipulação algébrica com o denominador de G ( s ) .

Passo 3

Faremos a manipulação algébrica do denominador ( 5 s - 1 ) ( τ V s + 1 ) ( τ T s + 1 ) no MATLAB mesmo. No script onde você definiu t _ V e t _ T , digite as linhas de código:

Na primeira linha, criamos uma variável simbólica s .

Na segunda linha, entramos com o denominador de G ( s ) , armazenando-o na variável d e n _ o r i g i n a l .

Na terceira linha, usamos o comando e x p a n d do MATLAB em d e n _ o r i g i n a l . Este comando multiplicará os termos de d e n _ o r i g i n a l e gerará o polinômio que precisamos, armazenando-o em d e n _ p o l .

Rodando o programa, temos:

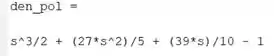
Passo 4

Agora que temos o polinômio do denominador de G ( s ) , podemos criar os vetores que servirão de entrada para t f . Para G ( s ) , o polinômio do numerador é 1 . Já o polinômio do denominador é 1 2 s 3 + 27 5   s 2 + 39 10 s - 1 .

No mesmo script onde você obteve d e n _ p o l , crie duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para t f . Como o polinômio do numerador tem somente um elemento correspondendo a 1 ∙ s 0 = 1 ∙ 1 = 1 , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de n u m e ela é igual a 1 .

A outra variável é um vetor chamado d e n , contendo os coeficientes de 1 2 s 3 + 27 5   s 2 + 39 10 s - 1 , indo do elemento com maior expoente ao de menor expoente:

Em seguida, adicione o comando abaixo para criar G ( s ) :

A função de transferência é armazenada na variável G . Você pode ver como G   ficou ao rodar o programa e pedir ao MATLAB para imprimir G no Command Window:

Note que as frações do denominador foram convertidas em números decimais, por isso que o denominador está um pouquinho diferente de d e n _ p o l . Apesar da forma diferente, é exatamente a mesma coisa.

Passo 5

Após criar G ( s ) , usaremos a função r l o c u s para plotar o lugar das raízes. r l o c u s tem a sintaxe:

r l o c u s ( f u n ç ã o   d e   t r a n s f e r ê n c i a )

A função r l o c u s tem como entrada uma função de transferência criada a partir do comando t f (no nosso caso, é a variável G ). Ao executarmos o programa, r l o c u s gera um gráfico com o lugar das raízes da função de trasnferência.

Adicione no seu script o comando:

Ao executar o programa, você terá o gráfico do lugar das raízes de G ( s ) :

Passo 6

Podemos encontrar a faixa de valores que K pode assumir no gráfico gerado no passo 5 . Para isto, devemos relembrar o critério de estabilidade: uma malha de controle é estável se as raízes forem números reais negativos ou se forem números complexos com a parte real negativa. No lugar das raízes, isso significa que as raízes devem estar à esquerda do eixo vertical.

Isso quer dizer que, para encontrarmos os valores do ganho K que garantem a estabilidade, devemos analisar os ramos que cruzam o eixo vertical. Logo, no nosso gráfico, a área de interesse é essa aqui:

Por isso, recomendo você ampliar o gráfico, dando um zoom nessa região, pra ver bem certinho os polos e os ramos. Você pode dar o zoom clicando no botão destacado em vermelho abaixo:

Para ver os valores de ganho, selecione o botão “Data Cursor” (destacado em azul acima) e clique sobre um dos ramos. Aparecerá um quadradinho preto com uma janelinha contendo informações sobre G ( s ) na naquele ponto:

O dado “Gain” é o que nos interessa. Ele representa o ganho K nesse ponto. Se você arrastar o quadradinho até um xizinho, que representa um polo, você verá que K = 0 quando o cursor estiver sobre o polo. Logo, quanto mais perto do polo, menor o K .

Repare que existe um polo à direita do eixo vertical, equivalente a 0,2 :

Como em K = 0 esse polo 0,2 é um número real positivo, que leva à instabilidade, a faixa de valores que o ganho deve assumir para que a malha seja estável não pode começar em 0 . Para definirmos qual o valor mínimo de K , devemos ver quanto ele vale exatamente sobre o eixo vertical, ou o mais próximo possível do eixo vertical que o MATLAB nos permita. Arraste o quadradinho preto sobre o ramo vermelho, sobre sua parte horizontal, e você terá:

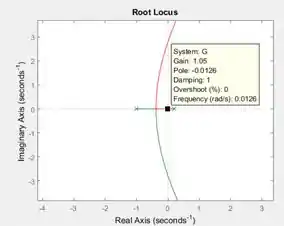
No ponto marcado acima, o polo se torna um número real negativo com um ganho K = 1,05 .

Para identificar o valor máximo que K pode assumir, continue arrastando o quadradinho preto sobre o ramo vermelho até que o ramo cruze novamente o eixo vertical, no limite em que a parte real do polo continue negativa:

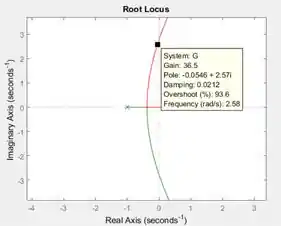
Temos que o valor máximo que K pode assumir é 36,5 .

Resposta

1,05 ≤ K ≤ 36,5

Exercício Resolvido #6

“UNICAMP – EA-721: Princípios de Controle e Servomecanismo. 2ª lista de exercícios, de José C. Geromel e Rubens H. Korogui. Exercício 12”

Considere a função de transferência de um sistema a tempo contínuo:

G s = 1 ( s + 2 ) ( s 2 + 8 s + 16 + α )

Para os valores do parâmetro α   ∈   { 1 ;   4 } , esboce no plano complexo o lugar das raízes da equação característica 1   +   κ G ( s )   =   0 , em função do ganho κ   ∈   [ 0 ,   + ∞ ) .

Passo 1

O exercício pede para esboçar o lugar das raízes de G ( s ) , usando dois valores distintos de α : 1 e 4 . Para fazermos o que o exercício pede, usaremos duas funções do MATLAB. Primeiro, vamos usar a função t f para entrar com G ( s ) . Em seguida, usaremos r l o c u s para plotar o lugar das raízes de G ( s ) .

Faremos esse procedimento duas vezes: uma vez para α = 1 e outra vez para α = 4 .

Passo 2

O primeiro passo é definir G ( s ) no MATLAB, usando a função t f , que tem a sintaxe:

s i s t e m a = t f ( n u m e r a d o r , d e n o m i n a d o r )

A função t f tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por n u m e r a d o r ) e outro contendo os coeficientes do polinômio do denominador (representado por d e n o m i n a d o r ). t f retorna um objeto representando a função de transferência, que será armazenada em s i s t e m a .

Contudo, repare que o denominador de G ( s ) está fatorizado. Para definirmos G ( s ) , vamos dividi-la em duas partes, G 1   e G 2 , de forma que G s = G 1 G 2 :

G 1 = 1 s + 2

G 2 = 1 s 2 + 8 s + 16 + α

Vamos começar definindo G 1 em um script novo do MATLAB, cujo numerador é 1 e o denominador é s + 2 . Vamos criar duas variáveis contendo os coeficientes dos polinômios de G 1 . A primeira variável representará os coeficientes do polinômio do numerador e será chamada de n u m _ G 1 . A segunda variável será um vetor chamado d e n _ G 1 e terá os coeficientes do polinômio do denominador. Após criar as duas variáveis de entrada de t f , digite o comando G 1 = t f ( n u m _ G 1 ,   d e n _ G 1 ) :

Desta forma, a função de transferência G 1 é criada e armazenada na variável G 1 .

Vamos fazer a mesma coisa para G 2 , começando com α = 1 , definido por meio do comando a l p h a = 1 :

Os vetores n u m _ G 2 e d e n _ G 2 contêm os coeficientes dos polinômios do numerador e do denominador de G 2 , respectivamente. Com a função t f , cria-se a funções de transferência G 2 .

Finalmente, para definir G ( s ) , inclua em seu código o produto abaixo:

Execute o programa para ver a cara de G , com α = 1 :

Passo 3

Após definir G ( s ) para α = 1 , use a função r l o c u s para plotar o lugar das raízes. r l o c u s tem a sintaxe:

r l o c u s ( f u n c a o _ t r a n s f e r e n c i a )

A função r l o c u s tem como entrada uma função de transferência criada a partir do comando t f (no nosso caso, é a variável G ). Ao executarmos o programa, r l o c u s gera um gráfico com o lugar das raízes da função de transferência.

Adicione no seu script o comando:

Ao executar o programa, você terá o gráfico do lugar das raízes de G ( s ) , quando α = 1 :

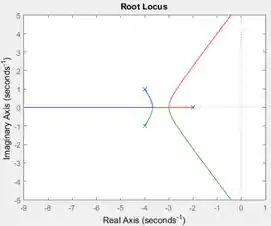
Passo 4

Vamos fazer o mesmo procedimento para α = 4 . No seu código, troque o valor da variável a l p h a de 1 para 4 , lá onde você criour G 2 :

Desta forma, G ( s ) ficará com essa cara:

E o lugar das raízes ficará assim:

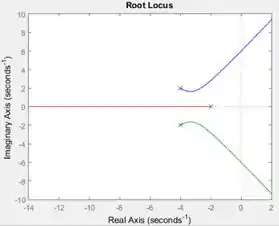
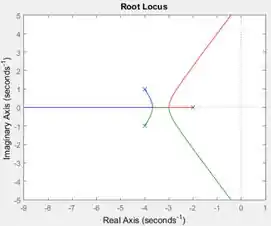
Resposta

α = 1 :

α = 4 :

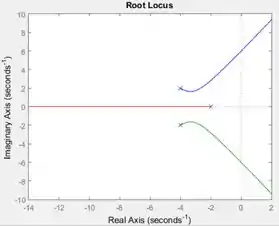
Exercício Resolvido #7

“Adaptado de UNICAMP – EA-721: Princípios de Controle e Servomecanismo. 2ª lista de exercícios, de José C. Geromel e Rubens H. Korogui. Exercício 14”

Considere um sistema de controle a tempo contínuo com realimentação unitária de acordo com a figura abaixo, na qual a planta é representada pela função de transferência

G s = ( s + 5 ) ( s + 10 ) s 2 ( s + 2 )

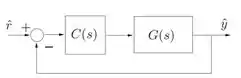
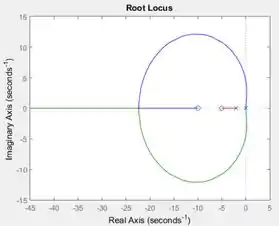
  1. Considerando um controlador C ( s )   =   κ   >   0 , esboce o lugar das raízes e determine os valores de κ para os quais o sistema em malha fechada seja estável.
  2. Para o controlador do item anterior, determine o parâmetro k de modo que o sistema em malha fechada possua dois polos complexos conjugados com fator de amortecimento igual a 0,707 .
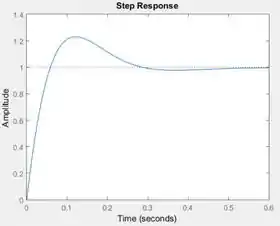
  3. Utilizando uma rotina computacional, obtenha a resposta ao degrau para o sistema em malha fechada, empregando o parâmetro k encontrado no item anterior.

Passo 1

O enunciado nos dá uma função de transferência G ( s ) e nos pede para esboçar o lugar das raízes, determinar a faxa de valores do ganho k em que o sistema é estável, encontrar o valor de k que dê um fator de amortecimento igual a 0 , 707 e, usando o k encontrado, determinar a saída do sistema para o degrau unitário.

Para plotar o lugar das raízes de G ( s ) no MATLAB e resolver a letra a do exercício, usaremos a função r l o c u s . A partir do lugar das raízes plotado, resolveremos as letras a e b, achando os valores de k no próprio gráfico. Com a resposta da letra b, faremos a letra c, gerando o sistema em malha fechada por meio do comando f e e d b a c k e plotando a resposta ao degrau unitário usando a função s t e p .

Passo 2

O primeiro passo é definir G ( s ) no MATLAB, usando a função t f , que tem a sintaxe:

s i s t e m a = t f ( n u m e r a d o r , d e n o m i n a d o r )

A função t f tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por n u m e r a d o r ) e outro contendo os coeficientes do polinômio do denominador (representado por d e n o m i n a d o r ). t f retorna um objeto representando a função de transferência, que será armazenada em s i s t e m a .

Contudo, repare que o numerador e o denominador de G ( s ) estão fatorizados. Para definirmos G ( s ) , vamos dividi-la em duas partes, G 1   e G 2 , de forma que G s = G 1 G 2 :

G 1 = s + 5 s 2

G 2 = s + 10 s + 2

Vamos começar definindo G 1 em um script novo do MATLAB, cujo numerador é s + 2 e o denominador é s 2 . Vamos criar duas variáveis contendo os coeficientes dos polinômios de G 1 . A primeira variável representará os coeficientes do polinômio do numerador e será chamada de n u m _ G 1 . A segunda variável será um vetor chamado d e n _ G 1 e terá os coeficientes do polinômio do denominador. Após criar as duas variáveis de entrada de t f , digite o comando G 1 = t f ( n u m _ G 1 ,   d e n _ G 1 ) :

Desta forma, a função de transferência G 1 é criada e armazenada na variável G 1 .

Vamos fazer a mesma coisa para G 2 :

Os vetores n u m _ G 2 e d e n _ G 2 contêm os coeficientes dos polinômios do numerador e do denominador de G 2 , respectivamente. Com a função t f , cria-se a funções de transferência G 2 .

Finalmente, para definir G ( s ) , inclua em seu código o produto abaixo:

Execute o programa para ver a cara de G :

Passo 3

Após definir G ( s ) , podemos resolver a letra a do exercício usando a função r l o c u s para plotar o lugar das raízes. r l o c u s tem a sintaxe:

r l o c u s ( f u n c a o _ t r a n s f e r e n c i a )

A função r l o c u s tem como entrada uma função de transferência criada a partir do comando t f (no nosso caso, é a variável G ). Ao executarmos o programa, r l o c u s gera um gráfico com o lugar das raízes da função de transferência.

Adicione no seu script o comando:

Ao executar o programa, você terá o gráfico do lugar das raízes de G ( s ) :

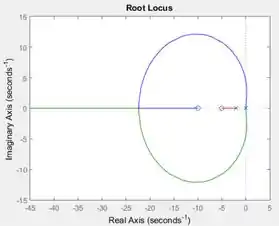
Passo 4

Podemos encontrar a faixa de valores que k pode assumir no gráfico gerado no passo 3 . Para isto, devemos relembrar o critério de estabilidade: uma malha de controle é estável se as raízes forem números reais negativos ou se forem números complexos com a parte real negativa. No lugar das raízes, isso significa que as raízes devem estar à esquerda do eixo vertical.

Isso quer dizer que, para encontrarmos os valores do ganho k que garantem a estabilidade, devemos analisar os ramos que cruzam o eixo vertical. Logo, no nosso gráfico, a área de interesse é essa aqui:

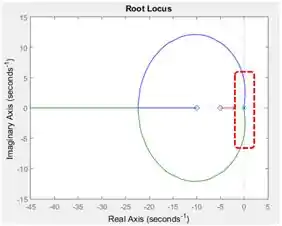
Por isso, recomendo você ampliar o gráfico, dando um zoom nessa região, pra ver bem certinho os polos e os ramos. Você pode dar o zoom clicando no botão destacado em vermelho abaixo:

Para ver os valores de ganho, selecione o botão “Data Cursor” (destacado em azul acima) e clique sobre um dos ramos. Aparecerá um quadradinho preto com uma janelinha contendo informações sobre G ( s ) na naquele ponto:

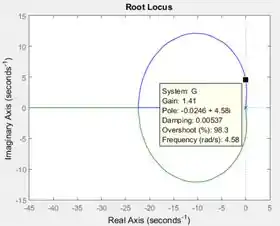
O dado “Gain” é o que nos interessa para responder à letra a. Ele representa o ganho k nesse ponto. Se você arrastar o quadradinho até um xizinho, que representa um polo, você verá que k = 0 quando o cursor estiver sobre o polo. Logo, quanto mais perto do polo, menor o k .

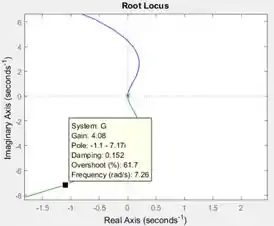
O polo bem na fronteira da estabilidade são polos iguais a 0 . Nesses polos, k = 0 e quando nos afastamos deles, k aumenta. O valor de k em um ponto bem em cima do eixo vertical é o valor mínimo que k tem que ter para que o sistema seja estável. O ganho k pode assumir qualquer valor acima desse mínimo, pois o restante do lugar das raízes encontra-se à esquerda do eixo vertical.

No seu gráfico do lugar das raízes, clique sobre um ponto bem em cima do eixo vertical, para encontrar o valor mínimo de k :

Para que o sistema em malha fechada seja estável, κ ≥ 1,41 . Letra a respondida ;)

Passo 5

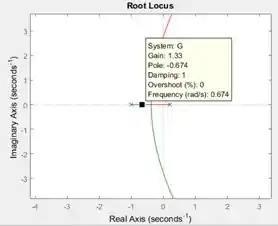
A partir do gráfico do lugar das raízes, vamos resolver a letra b do exercício, que pede para encontrarmos o ganho k para termos um fator de amortecimento igual a 0 , 707 .

No gráfico do lugar das raízes do MATLAB, clique sobre os ramos para ver as propriedades da função de transferência no ponto onde você clicou. Aqui, além do parâmetro “Gain”, que nos dá o valor de k , vamor ver o parâmetro “Damping”, que dá o fator de amortecimento.

Arraste o quadradinho preto que apareceu onde você clicou até encontrar um ponto onde o parâmetro “Damping” seja igual a 0 , 707 :

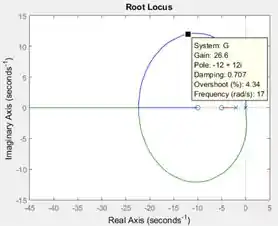
Temos que um ganho k = 26,6 nos dá um fator de amortecimento igual a 0 , 707 . Letra b resolvida ;D

Passo 6

A letra c pede para encontrarmos a resposta do sistema em malha fechada para um degrau unitário, considerando o ganho k = 26 , 6 encontrado na letra b. Para isto, usaremos o comando s t e p , que tem a sintaxe:

s t e p ( f u n c a o _ t r a n s f e r e n c i a )

A função s t e p plota o gráfico da resposta ao degrau unitário de f u n c a o _ t r a n s f e r e n c i a , que é uma função de transferência criada usando o comando t f .

Contudo, precisamos aplicar s t e p no sistema em malha fechada, como o diagrama do enunciado:

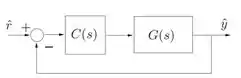
Para criar um sistema em malha fechada no MATLAB, usamos o comando f e e d b a c k , que tem a sintaxe:

m a l h a _ f e c h a d a = f e e d b a c k ( G s , H ( s ) )

O comando f e e d b a c k tem como entrada duas funções de transferência e retorna a função de transferência m a l h a _ f e c h a d a equivalente ao diagrama de blocos abaixo:

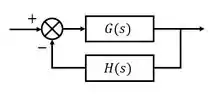
A primeira entrada de f e e d b a c k é a função de transferência da parte de cima do diagrama e a segunda entrada, é a função de transferência da parte de baixo.

No caso do exercício, quando usarmos a função f e e d b a c k , teremos que a primeira entrada é k * G e a segunda entrada é H ( s ) = 1 , pois se trata de um sistema com realimentação unitária.

Insira no seu código as duas linhas abaixo:

Na primeira linha, definimos o ganho k encontrado na letra b.

Na segunda linha, usamos o comando s t e p para plotar a resposta ao degrau do sistema com realimentação unitário, modelado por meio do comando f e e d b a c k .

Execute o programa e você terá a resposta da letra c.

Resposta

    2. κ ≥ 1,41

  2. k = 26,6

Exercício Resolvido #8

“Adaptado de UNICAMP – EA-721: Princípios de Controle e Servomecanismo. 2ª lista de exercícios, de José C. Geromel e Rubens H. Korogui. Exercício 17”

Considere o sistema de controle com realimentação unitária apresentado abaixo, no qual se assume κ > 0 . Para a função de transferência definida a seguir:

G s = 150 ( s + 4 ) ( s + 9 ) ( s 2 + 6 s + 13 ) ( s 2 + 16 s + 100 ) ( s + 7 )

  1. Esboce o lugar das raízes em função do ganho κ   >   0 .
  2. Determine κ   >   0 de maneira que os polos dominantes do sistema em malha fechada apresentem fator de amortecimento igual a 0,5 .
  3. Para κ determinado no item anterior, encontre a saída para uma entrada degrau unitário.

Passo 1

O enunciado nos dá uma função de transferência G ( s ) e nos pede para esboçar o lugar das raízes, determinar o ganho k de modo que os polos dominantes tenham fator de amortecimento igual a 0,5 (lembrando que os polos dominantes são aqueles que estão mais próximos do eixo imaginário do lugar das raízes, ou seja, do eixo vertical) e, usando o k encontrado, determinar a saída do sistema para o degrau unitário.

Para plotar o lugar das raízes de G ( s ) no MATLAB e resolver a letra a do exercício, usaremos a função r l o c u s . A partir do lugar das raízes obtido na letra a, resolveremos a letra b, achando o valor de k no próprio gráfico. Com a resposta da letra b, faremos a letra c, gerando o sistema em malha fechada por meio do comando f e e d b a c k e plotando a resposta ao degrau unitário por meio da função s t e p .

Passo 2

O primeiro passo é entrar com G ( s ) por meio da função t f , que tem a sintaxe:

s i s t e m a = t f ( n u m e r a d o r , d e n o m i n a d o r )

A função t f tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por n u m e r a d o r ) e outro contendo os coeficientes do polinômio do denominador (representado por d e n o m i n a d o r ). t f retorna um objeto representando a função de transferência, que será armazenada em s i s t e m a .

Contudo, repare que o numerador e o denominador de G ( s ) estão fatorizados. Para definirmos G ( s ) no MATLAB, vamos quebrá-la em três partes, G 1 , G 2 e G 3 , de forma que G s = G 1 G 2 G 3 :

G 1 = 150 s 2 + 6 s + 13

G 2 = s + 4 s 2 + 1 6 s + 1 00

G 3 = s + 9 s + 7

Vamos começar definindo G 1 em um script novo do MATLAB, cujo numerador é 1 50 . Já o denominador é o polinômio s 2 + 6 s + 13 . Vamos criar duas variáveis contendo os coeficientes dos polinômios de G 1 . A primeira variável representará os coeficientes do polinômio do numerador e será chamada de n u m _ G 1 . A segunda variável será um vetor chamado d e n _ G 1 e terá os coeficientes do polinômio do denominador. Após criar as duas variáveis de entrada de t f , digite o comando G 1 = t f ( n u m _ G 1 ,   d e n _ G 1 ) :

Desta forma, a função de transferência G 1 é criada e armazenada na variável G 1 .

Vamos fazer a mesma coisa para G 2 e G 3 :

Os vetores n u m _ G 2 e n u m _ G 3 contêm os coeficientes do polinômio do numerador de G 2   e G 3 , respectivamente. Já os vetores d e n _ G 2 e d e n _ G 3 contêm os coeficientes do polinômio do denominador de G 2   e G 3 , respectivamente. Com a função t f , criam-se as funções de transferência G 2 e G 3 .

Finalmente, para definir G ( s ) , inclua em seu código o produto abaixo:

Execute o programa para ver como G ficou:

Passo 3

Após definir G ( s ) , podemos resolver a letra a do exercício usando a função r l o c u s para plotar o lugar das raízes. r l o c u s tem a sintaxe:

r l o c u s ( f u n c a o _ t r a n s f e r e n c i a )

A função r l o c u s tem como entrada uma função de transferência criada a partir do comando t f (no nosso caso, é a variável G ). Ao executarmos o programa, r l o c u s gera um gráfico com o lugar das raízes da função de transferência.

Adicione no seu script o comando:

Ao executar o programa, você terá o gráfico do lugar das raízes de G ( s ) :

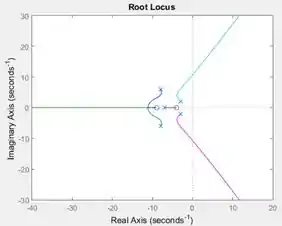
Pronto! Esta é a resposta da letra a =D

Passo 4

A partir do gráfico do lugar das raízes, vamos resolver a letra b do exercício, que pede para encontrarmos o ganho k de maneira que os polos dominantes do sistema em malha fechada apresentem fator de amortecimento igual a 0,5 .

No gráfico do lugar das raízes do MATLAB, as bolinhas representam os zeros e os chizinhos, os polos. Para vermos os parâmetros de G ( s ) nos polos dominantes, devemos clicar sobre os ramos partindo dos chizinhos mais próximos do eixo vertical, como no print abaixo:

Veja que abriu uma janelinha apresentando algumas propriedades da função de transferência no ponto onde clicamos. É nessa janelinha que vamos ver o valor de k , dado pelo parâmetro “Gain”, e o fator de amortecimento, que é dado pelo parâmetro “Damping”. No caso do print acima, para um ganho k = 0 , temos um fator de amortecimento de 0,832 .

Arraste o quadradinho preto que apareceu onde você clicou até encontrar um ponto onde o parâmetro “Damping” seja igual a 0,5 :

Temos que um ganho k = 1,66 nos dá um fator de amortecimento igual a 0,5 nos polos dominantes. Letra b resolvida ;D

Passo 5

A letra c pede para encontrarmos a resposta de G ( s ) para um degrau unitário, considerando o ganho k = 1,66 encontrado na letra b. Para isto, usaremos o comando s t e p , que tem a sintaxe:

s t e p ( f u n c a o _ t r a n s f e r e n c i a )

A função s t e p plota o gráfico da resposta ao degrau unitário de f u n c a o _ t r a n s f e r e n c i a , que é uma função de transferência criada usando o comando t f .

Contudo, precisamos aplicar s t e p no sistema em malha fechada, como o diagrama do enunciado:

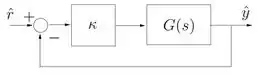
Para criar um sistema em malha fechada no MATLAB, usamos o comando f e e d b a c k , que tem a sintaxe:

m a l h a _ f e c h a d a = f e e d b a c k ( G s , H ( s ) )

O comando f e e d b a c k tem como entrada duas funções de transferência e retorna a função de transferência m a l h a _ f e c h a d a equivalente ao diagrama de blocos abaixo:

A primeira entrada de f e e d b a c k é a função de transferência da parte de cima do diagrama e a segunda entrada, é a função de transferência da parte de baixo.

No caso do exercício, quando usarmos a função f e e d b a c k , teremos que a primeira entrada é k * G e a segunda entrada é H ( s ) = 1 , pois se trata de um sistema com realimentação unitária.

Insira no seu código as duas linhas abaixo:

Na primeira linha, entramos com o ganho k encontrado na letra b.

Na segunda linha, usamos o comando s t e p para plotar a resposta ao degrau do sistema com realimentação unitário, modelado por meio do comando f e e d b a c k .

Execute o programa e você terá a resposta da letra c.

Resposta

  2. k = 1,66