Equações Diferenciais Ordinárias (EDO)
Teoria
Introdução
E aí, jovens do meu Brasil varonil? Tudo joia? Lembram das Equações Diferenciais Ordinárias, as temidas EDOs? Não?
Hoje vamos aprender a resolver EDOs e sistemas de EDOS no MATLAB. Mas antes de aprendermos mais uma função topzera do MATLAB, vamos dar uma relembrada rápida no que são EDOs.
Vamos começar com as EDOs de primeira ordem. Uma EDO de primeira ordem é uma equação que tem essa carinha:
onde é uma variável independente.
Como podemos ver na equação acima, uma EDO é uma equação que envolve uma função, sua derivada e uma variável independente. Resolvemos uma EDO para encontrar essa função, no caso, .
Para encontrarmos , precisamos integrar e isso normalmente gera uma família de funções. Para especificar uma única solução, usamos uma condição inicial, por exemplo:
A EDO de primeira ordem tem esse nome porque nela a derivada de maior ordem é a primeira derivada da função. Caso a EDO tivesse uma derivada segunda, ela seria de segunda ordem, e assim por diante.
“Tá, mas por que temos uma aula de MATLAB específica pra EDOs?”
O porquê, meu jovem gafanhoto, é que dependendo da EDO, não conseguimos resolvê-la analiticamente, na mão. Algumas podem ter umas funções bem diferentonas. Por isso, muitas vezes resolvemos as EDOs usando métodos numéricos. E o MATLAB já tem algumas funções prontas para resolver EDOs, baseadas nos métodos de Runge-Kutta.
“Runge o quê?”, você deve estar se perguntando.
Normalmente, a gente aprende os métodos de Runge-Kutta nas aulas de Cálculo Numérico. Eles são os métodos mais populares para solucionar EDOs.
Para entender esta aula de MATLAB sobre soluções de EDOs, você não precisa lembrar tintim por tintim desses métodos, só saber que eles existem e que o MATLAB usa eles para encontrar soluções numéricas de EDOs. Mas caso queira conhecer mais sobre os métodos de Runge-Kutta, aqui no Responde Aí tem uma aulinha bem legal sobre eles ;D
Resolvendo EDOs de primeira ordem no MATLAB
Depois de relembrarmos rapidinho o que é uma EDO, vamos ver como usar o MATLAB para calcular soluções numéricas para EDOs.
O MATLAB possui várias funções chamadas de para solucionar EDOs de primeira ordem, sendo a principal diferença entre elas a precisão do resultado final. Algumas funções dão soluções mais precisas, outras nem tanto.
Vamos ver nesta aula a função , que é a que o MATLAB recomenda, pois resolve a maior parte dos problemas de EDO e tem uma precisão boa, mas todas as funções têm uma sintaxe parecida.
A função tem o seguinte formato:
Vemos que ela exige três entradas:
- : uma função representando a EDO de primeira ordem ;
- : intervalo de integração, normalmente no formato : o intervalo começa em e termina em ;
- : condição inicial de em .
E ela nos dá duas saídas: um vetor com valores de (começando em e terminando em , correspondendo ao nosso intervalo de integração) e outro com os valores de (iniciando em e terminando no valor de correspondente a ), representando a solução da EDO. Em outras palavras, 𝑜𝑑𝑒45 nos retorna os os pontos que representam a função para o intervalo de integração .
Vamos de exemplo para ficar mais claro. Vamos resolver a EDO usando a :
No intervalo , assumindo como condição inicial
O primeiro passo é criar uma função no MATLAB representando a EDO:
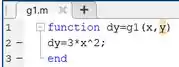
Neste print, é criada uma função chamada que recebe valores de e . Ela retorna , que é a derivada de e nossa EDO calculada para diversos valores de .
Em um novo script, entre com a função ode45 para encontrarmos a solução de :
Seguindo a estrutura de :
No lugar de 𝐸𝐷𝑂_𝑓𝑢𝑛, coloque o nome da função que você criou representando a EDO: ’. Não esqueça de pôr o nome entre aspas simples, como no print acima.
No lugar de , entre com o vetor de dois elementos , indicando o intervalo de integração. Neste caso, e .
No lugar de , entre com , que é a nossa condição inicial.
Ao rodarmos o programa, serão gerados os dois vetores e , representando a solução numérica da EDO.
Uma maneira legal de ver o resultado é por meio de gráficos, já que a nos retorna coordenadas. Neste exemplo, podemos também comparar a solução encontrada pela com a solução analítica de , que é:
Para isto, no mesmo script onde usamos a função , digite as linhas de código:
Na primeira linha, calculamos com a solução analítica da EDO para cada valor do vetor criado por e armazenamos o resultado no vetor .
Na segunda linha, geramos o gráfico com as curvas da solução analítica e da solução numérica, apresentado abaixo:
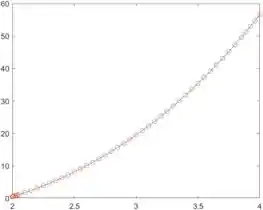
A curva azul é a solução analítica e as bolinhas vermelhas representam a solução numérica dada por . Viu como elas são bem próximas? :)
Sistemas de EDOs de primeira ordem
Agora, digamos que queremos resolver um sistema de EDOs como o abaixo:
Onde e .
As entradas e as saídas da função vão ser um pouquinho diferentes, mas o funcionamento segue a mesma lógica.
Vamos criar uma função no MATLAB, chamada de , representando o sistema de EDOs:
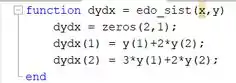
Como queremos encontrar duas funções ( e ), a entrada da função é um vetor de dois elementos, o primeiro elemento representando e o segundo elemento, . O vetor representando as derivadas das funções e , , também é um vetor de dois elementos.
Para resolver o sistema de EDOs, digite os seguintes comandos em um novo script do MATLAB:
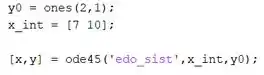
A primeira linha cria as condições iniciais de e . Elas são representadas por um vetor de dois elementos, . Se se tratasse de um sistema de EDOs com três EDOs, teria que ter três elementos, e assim por diante.
A segunda linha define o intervalo de integração da variável independente , que vai de a .
Em seguida, usamos a para resolver o sistema. A saída será um vetor , representando a variável independente, e uma matriz . A matriz tem duas colunas, a primeira representando e a segunda, . Se tivesse uma terceira função envolvida, esta matriz teria três colunas, entendeu?
Novamente, podemos ver o resultado do sistema de EDOs em forma de gráfico:
Este comando plota a primeira coluna da matriz em função de , representando . Ele também plota, no mesmo gráfico, uma curva dos valores da segunda coluna da matriz em função do vetor , representando .
Vamos ver como ficou? Rodando o programa, temos este lindo gráfico:
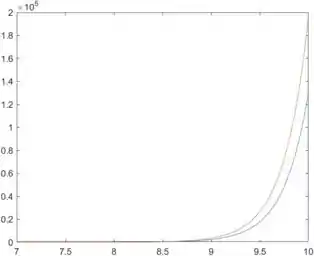
A curva em azul representa e a vermelha, .
E as EDOs de ordem superior?
Lembra que eu falei que o só resolve EDOs de primeira ordem? Por isso, para resolver EDOs de ordem superior no MATLAB, as transformamos em um conjunto de equações de primeira ordem.
Vamos de exemplo. Considere a EDO linear de segunda ordem:
Queremos encontrar . Para transformar a EDO de segunda ordem em um sistema de EDOs de primeira ordem, vamos definir duas novas funções:
Substituindo e na EDO original, conseguimos gerar um sistema de EDOs de primeira ordem:
Desta forma, podemos resolver o problema como fizemos na seção anterior. Vamos criar uma função no MATLAB chamada de com o sistema de EDOs de primeira ordem:
Vamos resolver o sistema de EDOs para o intervalo e com condições iniciais:
Para encontrarmos a solução do sistema de EDOs, criamos um novo script com as linhas de código:
A primeira linha de código define as condições iniciais para e e as armazena no vetor .
A segunda define o intervalo de integração no vetor de dois elementos .
A terceira linha usa a função para resolver o sistema de EDOs. Ela vai retornar o vetor , com valores de a , e a matriz , que possui duas colunas: uma representando , isto é, a primeira derivada , e outra coluna representando , que é a função que queríamos encontrar.
A quarta linha gera um gráfico contendo uma curva da primeira coluna de em função de e outra curva com os dados da segunda coluna de em função de . Em outras palavras, o gráfico terá uma curva representando , que é a primeira derivada da função , e outra representando , que é a própria função .
Rodando o programa, temos este gráfico maneiro:
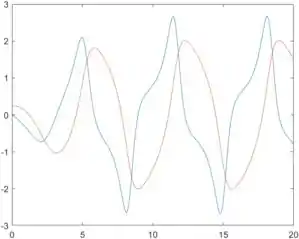
Em azul, temos a curva de , isto é, a curva de . Em vermelho, temos a curva de , que na verdade é a função que estávamos procurando.
Ufa! Vimos bastante coisa hoje, né? Agora é hora de praticar ;D Faça os exercícios que montei com muito carinho para ficar craque em resolver EDOs!
Resolvendo EDOs de primeira ordem no MATLAB
Sistemas de EDOs de primeira ordem
E as EDOs de ordem superior?
Exercícios Resolvidos
Exercício Resolvido #1
“UERJ - Curso de MATLAB 5.1: Introdução à Solução de Problemas de Engenharia, Laboratório de Engenharia Elétrica, p. 133”
Seja a equação:
- Assumindo como condição inicial , resolva, no MATLAB, essa equação diferencial no intervalo de e plote o gráfico com os valores correspondentes de .
- Sendo a solução analítica para esta equação, faça um novo gráfico que compare a solução analítica com a numérica.
Passo 1
O exercício nos dá uma EDO, uma condição inicial e um intervalo e nos pede para encontrar a solução da EDO . Essas são as três entradas da função do MATLAB, que resolve EDO de primeira ordem usando métodos de Runge-Kutta.
Em seguida, ele nos pede para gerarmos um gráfico de . As saídas da função são valores de e , representando a solução da EDO. Essas saídas podem ser usadas para plotar o gráfico de .
Portanto, usaremos para resolver a letra a do exercício.
A letra b dá a solução analítica da EDO e pede para gerar um novo gráfico comparando as curvas da solução analítica e da solução numérica, isto é, a solução obtida usando na letra a.
Passo 2
Primeiramente, vamos relembrar a função , para vermos o que entraremos no MATLAB. A função possui a seguinte estrutura:
Ela exige três entradas:
- : uma função representando a EDO de primeira ordem . Neste exercício, é a EDO ;
- : intervalo de integração, normalmente no formato : o intervalo começa em e termina em . Neste exercício, e , logo, ;
- : condição inicial de em . Neste exercício, .
E ela nos dá duas saídas: um vetor com valores de (começando em e terminando em , correspondendo ao nosso intervalo de integração) e outro com os valores de (iniciando em e terminando no valor de correspondente a ), representando a solução da EDO. Em outras palavras, 𝑜𝑑𝑒45 nos retorna os pontos que representam a função para o intervalo de integração . Usaremos os vetores e para gerar o gráfico pedido na letra a.
Agora, crie um script novo no MATLAB para criarmos uma função com a EDO do enunciado. Nesse script, digite as linhas de código:
Com estas linhas de código, é criada a função , representando a EDO do enunciado. Ela recebe valores de e e retorna a derivada .
Após criar a função , abra um novo script para implementar a função . Neste script, digite as linhas de código:
Na primeira linha, entramos com o intervalo de integração .
Na segunda linha, entramos com o valor inicial .
Na terceira linha, entramos com a função para encontrar uma solução da EDO. Repare que, no lugar de 𝐸𝐷𝑂_𝑓𝑢𝑛, coloquei um string com o nome da função que representa a EDO: ’. Não esqueça de pôr o nome entre aspas simples, como no print acima.
A solução da EDO é dada pelos vetores e , saídas de .
Passo 3
Com os códigos do passo 2, encontramos a solução da EDO. Mas falta ainda uma coisinha: gerar o gráfico de . Para isto, usaremos a saída de os vetores e .
No mesmo script onde você implementou , digite as linhas de código:
Na primeira linha, pedimos ao MATLAB para criar uma figura de índice 1. Fazemos isso já prevendo que mais para frente plotaremos outro gráfico, para a letra b do exercício, e quermos que estes gráficos sejam gerados em janelas diferentes.
O comando na segunda linha efetivamente gera o gráfico da solução da EDO.
Rode seu programa e você terá este lindo gráfico:
Pronto! Letra a respondida ;)
Passo 4
Vamos responder à letra b do exercício. Ela nos diz que a solução analítica de é:
E pede para gerarmos um gráfico comparando a solução analítica com a numérica, obtida na letra a.
A primeira coisa a fazer é gerar valores de da solução analítica para plotar a curva. Para isto, no mesmo script onde você resolveu a letra a, digite a linha de código:
Esta linha de código é a função . Ela usa o vetor gerado pela e calcula a solução analítica para cada elemento de . Os resultados são armazenados no vetor .
Em seguida, para gerar o gráfico comparando a solução analítica com a numérica, entre os comandos:
Na primeira linha, pedimos ao MATLAB para gerar uma figura com índice 2. Este comando serve para gerar os gráficos das letras a e b em janelas diferentes.
Na segunda linha, é usado o para gerar as curvas da solução analítica e da solução numérica. O primeiro par plota a solução analítica em função de . O segundo par plota a solução numérica em função de , e pede que a curva gerada seja composta por bolinhas ().
Na terceira linha, é adicionada uma legenda ao gráfico, para sabermos qual curva é qual. A legenda corresponde ao primeiro par e a legenda , ao segundo par .
Basta rodar o programa que você terá a solução da letra b :)
Resposta
A curva azul representa a solução analítica e a curva composta por círculos vermelhos corresponde à solução numérica.
Exercício Resolvido #2
“Adaptado de UNICAMP - Exercícios de Cálculo Numérico - Prof. R. Biloti - 29.04.2021”
Dado o Problema de Valor Inicial (PVI) abaixo:
, ,
- Reescreva o PVI como um sistema de equações diferenciais de primeira ordem;
- Resolva o sistema de EDO e plote a função e sua primeira derivada.
Passo 1
O enunciado nos dá uma EDO de segunda ordem (tem uma segunda derivada na equação) e primeiro nos pede para convertê-la em um sistema de EDOs de primeira ordem.
Esta etapa é necessária para respondermos à letra b usando o MATLAB, que só resolve EDOs de primeira ordem. A letra b nos pede para resolver o sistema de EDOs de primeira ordem construído na letra a e gerar gráficos da solução do sistema, que é a função , e de sua primeira derivada.
Resolveremos o sistema de EDOs criado na letra a com a função . O enunciado também nos deu todas entradas necessárias para usarmos ode45: um intervalo de integração e valores iniciais para a função e sua derivada primeira.
Passo 2
Vamos começar com a letra a. Para converter em um sistema de EDOs de primeira ordem, vamos dizer que:
Substituindo e na EDO original, temos:
Isolando na equação acima, temos:
Esta é a primeira equação do sistema de EDOs de primeira ordem.
Para construir a segunda equação do sistema, considere que:
Logo, o sistema de EDOs de primeira ordem construído a partir de é:
Pronto! Letra a resolvida.
Passo 3
A letra b pede para resolver o sistema de EDOs de primeira ordem obtido na letra a. Para isto, usaremos a função do MATLAB, que tem a estrutura:
Ela tem três entradas:
- : uma função representando o sistema de EDOs de primeira ordem, no caso:
- : intervalo de integração, normalmente no formato : o intervalo começa em e termina em . Neste exercício, , , logo ;
- : vetor com as condições iniciais de e em .
Como , temos que e . Logo, .
A função nos dará duas saídas: um vetor com valores de (começando em e terminando em , correspondendo ao nosso intervalo de integração) e uma matriz de duas colunas com os valores de e (iniciando em e terminando nos valores de e correspondentes a ), representando a solução do sistema de EDOs. A primeira coluna de corresponde a e a segunda coluna de corresponde a .
Em outras palavras, 𝑜𝑑𝑒45 nos retorna os pontos que representam a função , na forma de , e sua primeira derivada, na forma de , para o intervalo de integração .
Bora implementar tudo isso no MATLAB. Abra um script novo e crie a função , com o sistema de EDOs obtido na letra a:
Como queremos encontrar duas funções ( e ), a entrada da função é um vetor de dois elementos, o primeiro elemento representando e o segundo elemento, . O vetor representando as derivadas das funções e , , também é um vetor de dois elementos.
Para resolver o sistema de EDOs, digite os seguintes comandos em um novo script do MATLAB:
A primeira linha cria o intervalo de integração .
A segunda linha cria as condições iniciais de e . Elas são representadas por um vetor de dois elementos, .
Em seguida, usamos a para resolver o sistema. Repare que no lugar de coloquei uma string . Essa string é o nome da função criada para representar o sistema de EDOs.
A saída de será um vetor , representando a variável independente, e uma matriz com duas colunas, a primeira representando e a segunda, . A saída representa a solução do sistema de EDOs.
Passo 4
Após obtermos a solução do sistema EDOs, podemos gerar as curvas de e de sua primeira derivada, , usando as saídas de . Como a 𝑜𝑑𝑒45 nos retorna os pontos que representam na primeira coluna de e os pontos que representam na segunda coluna de , consequentemente temos e .
Para plotar e , entre os seguintes comandos no script onde você usou a função :
Na primeira linha, usamos a função para gerar, em um mesmo gráfico, as curvas de e . O primeiro par pega a segunda coluna de , correspondendo a , isto é, a , e a plota em função de . Da mesma maneira, o segundo par pega a primeira coluna de , correspondendo a , isto é, a , e a plota em função de .
Na segunda linha, acrescentamos uma legenda ao gráfico, indicando que o par representa e o par representa .
Para obter o resultado da letra b, rode o programa.
Resposta
Exercício Resolvido #3
“Adaptado de UERJ - Curso de MATLAB 5.1: Introdução à Solução de Problemas de Engenharia, Laboratório de Engenharia Elétrica, p. 133”
Uma avançada turbina chamada de ventilador não canalizado (UDF) é uma das novas tecnologias mais promissoras que tem sido desenvolvida para o futuro transporte de aeronaves.
Turbinas, que têm sido usadas por décadas, combinam o poder e a confiabilidade dos motores a jato com a eficiência dos propulsores. Eles constituem uma importante melhoria dos antigos propulsores movidos a pistão. Suas aplicações têm sido limitadas a pequenas aeronaves do tipo comutador, isto porque eles não são tão rápidos, nem poderosos quanto as turbinas usadas em grandes aeronaves. Esse tipo de turbina (UDF) implica em avanços significantes na tecnologia de propulsão. Novos materiais, aerodinâmica e velocidades de alta rotação habilitam esta turbina a voar tão rápido quanto as turbinas a jato, e com grande aproveitamento de combustível. A UDF é também menos barulhenta que o sistema convencional de turbinas.
Durante um teste de vôo de uma turbina UDF de uma aeronave, o motor é levado para um nível de , o que significa os da aeronave tendo alcançado uma velocidade de . As válvulas de regulação do motor são então levadas para atingir um nível de , e a aeronave começa a acelerar.
A equação diferencial que determina a aceleração da aeronave é:
Onde:
nível atingido em
massa em
velocidade em
Escreva no MATLAB um programa para determinar a nova velocidade depois de uma mudança no nível do motor através do gráfico da solução para a equação diferencial. Considere um intervalo de tempo de 6 min.
Passo 1
O enunciado nos dá a seguinte EDO de primeira ordem:
Substituindo por , que é o valor da massa da aeronave, temos a EDO:
Onde é o nível do motor em , o tempo em é a variável independente e , a velocidade da aeronave em , é a função que queremos descobrir resolvendo a EDO.
O enunciado diz que quando o nível do motor é , a aeronave atinge uma velocidade de . Em seguida, o nível do motor sobe para . Ao final, nos é perguntado qual é a velocidade da aeronave com o motor atinge um nível de . Para encontrar esta velocidade, temos que considerar na EDO acima. Logo, a EDO que temos que encontrar uam solução é:
De maneira indireta, o enunciado nos dá o intervalo de integração e a condição inicial para resolver a EDO.
O enunciado nos diz pra considerarmos um intervalo de 6 min. Considerando o instante inicial de e o final , temos que o intervalo de integração é .
O enunciado diz que a aeronave tem uma velocidade de quando o nível do motor vai para . Logo, a condição inicial é .
Portanto, temos todas as entradas necessárias para usar a função do MATLAB.
Além disso, o exercício pede para mostrarmos no gráfico da solução da EDO a velocidade que a aeronave atinge quando o nível do motor é . Por isso, no final, também teremos que gerar um gráfico de considerando .
Passo 2
Primeiramente, vamos relembrar a função , para vermos o que entraremos no MATLAB. A função possui a seguinte estrutura:
Ela exige três entradas, fornecidas pelo enunciado:
- : uma função representando a EDO de primeira ordem:
- : intervalo de integração, normalmente no formato : o intervalo começa em e termina em . Neste exercício, e , logo, ;
- : condição inicial de em . Neste exercício, .
E ela nos dá duas saídas: um vetor com valores de (começando em e terminando em , correspondendo ao nosso intervalo de integração) e outro com os valores de (iniciando em e terminando no valor de correspondente a ), representando a solução da EDO. Em outras palavras, 𝑜𝑑𝑒45 nos retorna os pontos que representam a função para o intervalo de integração . Usaremos os vetores e para gerar o gráfico pedido.
Depois de relembrar a função , vamos abrir um script novo no MATLAB para criarmos uma função com a EDO do enunciado. Nesse script, digite as linhas de código:
Após criar a função , abra um novo script para implementar a função . Neste script, digite as linhas de código:
Na primeira linha, entramos com o intervalo de integração .
Na segunda linha, entramos com o valor inicial .
Na terceira linha, entramos com a função para encontrar uma solução da EDO. Repare que, no lugar de 𝐸𝐷𝑂_𝑓𝑢𝑛, coloquei um string com o nome da função que representa a EDO: ’. Não esqueça de pôr o nome entre aspas simples, como no print acima.
A solução da EDO é dada pelos vetores e , saídas de .
Passo 3
Com os códigos do passo 2, encontramos a solução da EDO. Mas falta ainda uma coisinha: gerar o gráfico de . Para isto, usaremos a saída de os vetores e .
No mesmo script onde você implementou , digite as linhas de código:
A primeira linha gera o gráfico da velocidade em função do tempo.
A segunda linha dá um nome para o eixo horizontal do gráfico, usando a função . Foi dado um nome de .
A terceira linha dá um nome para o eixo vertical do gráfico, usando a função . Foi dado um nome de .
Ao rodar o programa, o gráfico de tempo versus velocidade é gerado e nele podemos encontrar a resposta do exercício:
Repare que a curva se estabiliza em torno de . Isto quer dizer que a nova velocidade da aeronave depois de uma mudança no nível do motor de para é .
Resposta
A nova velocidade da aeronave depois de uma mudança no nível do motor de para é .
Exercício Resolvido #4
“Adaptado de UNICAMP - Exercícios de Cálculo Numérico - Prof. R. Biloti - 29.04.2021”
Utilize um método de Runge-Kutta explícito para aproximar , sabendo que
Passo 1
O exercício nos dá uma EDO de primeira ordem e uma condição inicial: . Ele pede para encontrarmos usando um método de Runge-Kutta explícito.
Para encontrarmos , precisamos solucionar a EDO para encontrar . Como o exercício pede para usarmos um método de Runge-Kutta explícito, podemos usar a função do MATLAB, que resolve EDOs de primeira ordem usando um método explícito de Runge-Kutta.
Como temos uma condição inicial em () e o exercício pede para encontrarmos , temos que e nosso intervalo de integração vai ser .
Resumindo, neste exercício, usaremos a função para resolver a EDO e então encontrar .
Passo 2
A primeira coisa que devemos fazer é rearranjar os termos da EDO do enunciado:
Para que ela fique no formato:
Reorganizando os termos, temos:
É a EDO neste formato que usaremos na função do MATLAB.
Passo 3
Vamos relembrar a função , para vermos o que entraremos no MATLAB. A função possui a seguinte estrutura:
Ela exige três entradas:
- : uma função representando a EDO de primeira ordem . Neste exercício, é a EDO ;
- : intervalo de integração, normalmente no formato : o intervalo começa em e termina em . Neste exercício, e , logo, ;
- : condição inicial de em . Neste exercício, .
A fnção nos dá duas saídas: um vetor com valores de (começando em e terminando em , correspondendo ao nosso intervalo de integração) e outro com os valores de (iniciando em e terminando no valor de correspondente a ), representando a solução da EDO. Em outras palavras, 𝑜𝑑𝑒45 nos retorna os pontos que representam a função para o intervalo de integração .
Crie um script novo no MATLAB para criarmos uma função com a EDO do enunciado. Nesse script, digite as linhas de código:
Com estas linhas de código, é criada a função , representando a EDO do enunciado. Ela recebe valores de e e retorna a derivada .
Após criar a função , abra um novo script para implementar a função . Neste script, digite as linhas de código:
Na primeira linha, entramos com o intervalo de integração .
Na segunda linha, entramos com o valor inicial .
Na terceira linha, entramos com a função para encontrar uma solução da EDO. Repare que, no lugar de 𝐸𝐷𝑂_𝑓𝑢𝑛, coloquei um string com o nome da função que representa a EDO: ’. Não esqueça de pôr o nome entre aspas simples, como no print acima.
A solução da EDO é dada pelos vetores e , saídas de .
Passo 4
Para encontrarmos , temos que olhar o último elemento do vetor , pois ele corresponde ao valor da função no final do intervalo .
No mesmo script onde implementamos a função , vamos adicionar o comando:
Com este comando, o último elemento do vetor , indicado pelo índice , é armazenado na variável . Portanto, , que é a resposta do exercício.
Rodando o programa, temos:
Resposta
Exercício Resolvido #5
“UFRJ – MATLAB: Dicas iniciais de utilização – PEQ/COPPE/UFRJ- Janeiro de 2003. Exercícios Série D, p. 38”
Considere o reator bioquímico descrito na figura abaixo, onde representa a biomassa presente no reator e o substrato. O reator possui um volume constante () uma vez que as vazões de alimentação e de saída são iguais (). A corrente de alimentação possui concentração de substrato igual a x2i e uma concentração de biomassa igual a zero.
Bequette (1998) propõe o modelo descrito pela equação abaixo para o processo:
onde é a relação constante entre as taxas de geração de biomassa e o consumo de substrato e é o coeficiente de taxa de crescimento descrito pela equação:
Descreva o comportamento das concentrações de biomassa e de substrato considerando um tempo de integração de 30 horas (), as condições iniciais:
E os valores para os parâmetros descritos na tabela abaixo:
BEQUETTE, B. W., Process Dynamics: Modeling, Analysis and Simulation, 1a ed. USA, PrenticeHall PTR, 1998.
Passo 1
O exercício nos dá um sistema de EDOs de primeira ordem, composto de duas EDOs, representando as concentrações de biomassa () e de substrato () presentes em um reator bioquímico.
O enunciado pede para resolvermos o sistema de EDOs em um intervalo de integração de a horas, isto é, o intervalo de integração é .
Para resolvermos o sistema de EDOs, temos como condições iniciais:
Portanto, temos todas as entradas para usarmos a função do MATLAB para encontrarmos a solução do sistema de EDOs.
O exercício pede para descrevermos o comportamento das concentrações de biomassa e de substrato, isto é, de e , respectivamente, no intervalo de horas. Por isso, é legal no final gerarmos um gráfico com as curvas de e , plotadas usando o resultado da .
Passo 2
Vamos começar relembrando a função do MATLAB, que tem a estrutura:
Ela tem três entradas:
- : uma função representando o sistema de EDOs de primeira ordem, no caso:
- : intervalo de integração, normalmente no formato : o intervalo começa em e termina em . Neste exercício, , , logo ;
- : vetor com as condições iniciais de e em . Temos que , logo, .
A função nos dará duas saídas: um vetor com valores de (começando em e terminando em , correspondendo ao nosso intervalo de integração) e uma matriz de duas colunas com os valores de e (iniciando em e terminando nos valores de e correspondentes a ), representando a solução do sistema de EDOs. A primeira coluna de corresponde a e a segunda coluna de corresponde a .
Em outras palavras, 𝑜𝑑𝑒45 nos retorna os pontos que representam de e para o intervalo de integração .
Vamos implementar tudo isso no MATLAB. Primeiramente, abra um script novo e crie a função . Vamos entrar com os dados da tabela do enunciado, com as seguintes linhas de código:
Como queremos encontrar duas funções ( e ), a entrada da função é um vetor de dois elementos, o primeiro elemento representando e o segundo elemento, . A saídade é um vetor representando as derivadas das funções e e também é um vetor de dois elementos.
Em seguida, entre com a equação do coeficiente de taxa de crescimento:
Digitando a linha de código:
Tendo entrado com a equação de , finalmente podemos entrar com o sistema de EDOs:
No final, a função ficou com essa carinha:
Passo 3
Após concluir a função , vamos resolver o sistema de EDOs. Digite os seguintes comandos em um novo script do MATLAB:
A primeira linha cria o intervalo de integração .
A segunda linha cria as condições iniciais de e . Elas são representadas por um vetor de dois elementos, .
Em seguida, usamos a para resolver o sistema. Repare que no lugar de coloquei uma string . Essa string é o nome da função criada para representar o sistema de EDOs.
A saída de será um vetor , representando a variável independente, e uma matriz com duas colunas, a primeira representando e a segunda, . A saída representa a solução do sistema de EDOs.
Passo 4
O exercício pede para analisarmos o comportamento das concentrações de biomassa e de substrato, isto é, de e , respectivamente, no intervalo de horas. Por isso, vamos gerar um gráfico com as curvas de e , usando os vetores de saída e da .
Para plotar e , entre os seguintes comandos no script onde você usou a função :
Na primeira linha, usamos a função para gerar, em um mesmo gráfico, as curvas de e . O primeiro par pega a primeira coluna de , correspondendo a e a plota em função de . Da mesma maneira, o segundo par pega a segunda coluna de , correspondendo a e a plota em função de .
Na segunda linha, acrescentamos uma legenda ao gráfico, indicando que o par representa a concentração de biomassa e o par representa a concentração de substrato.
Na terceira linha, damos um nome para o eixo horizontal do gráfico usando o comando . O nome indica que no eixo horizontal temos o tempo em horas.
Na quarta linha, damos um nome para o eixo vertical do gráfico usando o comando . O nome indica que no eixo vertical temos a concentração em gramas/litro.
Rodando o programa, o gráfico será gerado e podemos analisar o comportamento da biomassa e do substrato.
Resposta
O gráfico acima contém as curvas de concentração de biomassa (, em azul) e de substrato (, em vermelho), em um reator bioquímico, para um intervalo de a horas.
No começo, nas primeiras horas, a concentração de biomassa aumenta, enquanto a de substrato diminui. Após as primeiras horas, as concentrações de biomassa e substrato se estabilizam e tornam-se constantes.
Exercício Resolvido #6
“USP – Sistemas Dinâmicos I: Usando a Ferramenta MATLAB, de Eduardo L.L. Cabral e Larissa Driemeier. Seção 9.5, exercício 3, p. 59”
O modelo do circuito RC mostrado na figura abaixo pode ser encontrado a partir da lei das tensões de Kirchhoff e da conservação da carga:
Suponha que o valor de seja . Utilize um método numérico para encontrar a resposta para o caso em que a tensão externa aplicada é zero e que a tensão inicial do capacitor seja . Compare os resultados com a solução analítica, que é
Passo 1
O exercício nos dá uma EDO que modela um cicuito RC e uma condição inicial, e nos pede para encontrar a solução da EDO , que representa a tensão do capacitor. O enunciado não nos dá um intervalo de integração, representando o tempo , mas podemos escolher um intervalo qualquer. Uma EDO, uma condição inicial e um intervalo de integração são as três entradas da função do MATLAB, que resolve EDOs de primeira ordem usando métodos de Runge-Kutta. Logo, usaremos essa função para encontrar .
Em seguida, ele nos pede para compararmos a solução encontrada com , isto é, a solução numérica da EDO, à solução analítica. Para isto, geraremos um gráfico com duas curvas: uma representando a solução obtida por e a outra representando a solução analítica.
Passo 2
Primeiramente, vamos relembrar a função , para vermos o que entraremos no MATLAB. A função possui a sintaxe:
Ela exige três entradas:
- : uma função representando a EDO de primeira ordem . Neste exercício, é a EDO ;
- : intervalo de integração, normalmente no formato : o intervalo começa em e termina em . O enunciado não especificou o intervalo de integração, por isso podemos escolher o intervalo que quisermos. Vamos adotar e , logo, ;
- : condição inicial de em . Neste exercício, .
A função nos dá duas saídas: um vetor com valores de (começando em e terminando em , correspondendo ao nosso intervalo de integração) e outro com os valores de (iniciando em e terminando no valor de correspondente a ), representando a solução da EDO. Em outras palavras, 𝑜𝑑𝑒45 nos retorna os pontos que representam a função para o intervalo de integração . Usaremos os vetores e para gerar o gráfico comparando a solução numérica com a solução analítica.
Vamos começar pela função representando a EDO. O primeiro passo é reorganizar os termos a EDO do enunciado, de forma que a derivada fique isolada no lado esquerdo da EDO. Lembrando que :
Agora podemos passar a EDO para o MATLAB. Crie um script novo e digite as linhas de código:
Com estas linhas de código, é criada a função , representando a EDO do enunciado. Ela recebe valores de e e retorna a derivada .
Passo 3
Após criar a função , abra um novo script para implementar a função . Lembre de salvá-lo na mesma pasta onde você salvou a função . Neste script, digite as linhas de código:
Na primeira linha, entramos com o intervalo de integração .
Na segunda linha, entramos com o valor inicial .
Na terceira linha, entramos com a função para encontrar uma solução da EDO. Repare que, no lugar de 𝐸𝐷𝑂_𝑓𝑢𝑛, coloquei um string com o nome da função que representa a EDO: . Não esqueça de pôr o nome entre aspas simples, como no print acima.
A solução da EDO é dada pelos vetores e , saídas de . Esses vetores representam a solução numérica da EDO, a qual plotamos a partir deles.
Passo 4
O exercício pede para compararmos a solução numérica da EDO com a solução analítica, dada por:
Vamos compará-las por meio de um gráfico. A primeira coisa a fazer é gerar valores de da solução analítica para plotar sua curva. Para isto, no mesmo script onde você implementou , digite a linha de código:
Esta linha de código é a função . Ela usa o vetor gerado pela e calcula a solução analítica para cada elemento de . Os resultados são armazenados no vetor .
Passo 5
Para gerar o gráfico comparando a solução analítica com a numérica, entre os comandos:
Na primeira linha, é usado o para gerar as curvas da solução analítica e da solução numérica. O primeiro par plota a solução analítica em função de . O segundo par plota a solução numérica em função de , e pede que a curva gerada seja composta por bolinhas ().
Na segunda linha, é adicionada uma legenda ao gráfico, para sabermos qual curva é qual. A legenda corresponde ao primeiro par e a legenda , ao segundo par .
Execute o programa e você terá o gráfico que permite comparar as duas soluções.
Resposta
Exercício Resolvido #7
“Adaptado de UNICAMP - Exercícios de Cálculo Numérico - Prof. R. Biloti – Exercício 25.3 (29.04.2021)”
Considere o sistema de equações diferenciais de primeira ordem com condições iniciais, dado por
Este sistema modela a interação entre duas populações, uma de presas e outra de predadores. Faça o gráfico de e , para
Passo 1
O exercício nos dá um sistema de EDOs de primeira ordem, composto de duas EDOs, modelando a interação entre duas populações e .
O enunciado pede para resolvermos o sistema de EDOs em um intervalo de integração de a , isto é, o intervalo de integração é .
Para resolvermos o sistema de EDOs, temos como condições iniciais e .
Portanto, temos todas as entradas para usarmos a função do MATLAB para encontrarmos a solução do sistema de EDOs.
O exercício pede para gerarmos o gráfico de e , plotadas usando o resultado da .
Passo 2
Vamos começar relembrando a função do MATLAB, que tem a estrutura:
Ela tem três entradas:
- : uma função representando o sistema de EDOs de primeira ordem, no caso:
- : intervalo de integração, normalmente no formato : o intervalo começa em e termina em . Neste exercício, , , logo ;
- : vetor com as condições iniciais de e em . Temos que e , por isso faremos que .
A função nos dará duas saídas: um vetor com valores de (começando em e terminando em , correspondendo ao nosso intervalo de integração) e uma matriz de duas colunas com os valores de e (iniciando em e terminando nos valores de e correspondentes a ), representando a solução do sistema de EDOs. A primeira coluna de corresponde a e a segunda coluna de corresponde a .
Em outras palavras, 𝑜𝑑𝑒45 nos retorna os pontos que representam de e para o intervalo de integração .
Vamos implementar tudo isso no MATLAB. Primeiramente, abra um script novo e crie a função . Vamos entrar com o sistema de equações, com as seguintes linhas de código:
Como queremos encontrar duas funções ( e ), a entrada da função é um vetor de dois elementos, o primeiro elemento representando e o segundo elemento, . Para facilitar a identificação de quem é quem na hora de digitar o sistema de EDOs, nas duas primeiras linhas da função, criei duas variáveis: e e indiquei que elas são o primeiro e o segundo elemento do vetor , respectivamente.
O vetor representando as derivadas das funções e , , também é um vetor de dois elementos, sendo que o primeiro representa e o segundo, . Por isso, na terceira linha da função, dizemos que é um vetor de zeros de dois elementos.
Finalmente, nas duas últimas linhas de código, temos o sistema de EDOs do enunciado.
Passo 3
Após concluir a função , vamos resolver o sistema de EDOs. Digite os seguintes comandos em um novo script do MATLAB (que deve sr salvo na mesma pasta onde foi salva a função):
A primeira linha cria o intervalo de integração .
A segunda linha cria as condições iniciais de e . Elas são representadas por um vetor de dois elementos, .
Em seguida, usamos a para resolver o sistema. Repare que no lugar de coloquei uma string . Essa string é o nome da função criada para representar o sistema de EDOs.
A saída de será um vetor , representando a variável independente , e uma matriz com duas colunas, a primeira representando e a segunda, . A saída representa a solução do sistema de EDOs e a partir delas que plotaremos os gráficos de e .
Passo 4
Para facilitar a identificação na hora de plotar e , inclua em seu script as duas linhas de código abaixo:
Na primeira linha, crio um vetor que armazena a primeira coluna de , que representa obtida pela integração numérica de .
Na segunda linha, faço a mesma coisa para : crio um vetor que armazena a segunda coluna de , que é gerada por .
Para plotar e , entre os seguintes comandos no script onde você usou a função :
Na primeira linha, usamos a função para gerar, em um mesmo gráfico, as curvas de e . O primeiro par plota em função de . Da mesma maneira, o segundo par plota em função de .
Na segunda linha, acrescentamos uma legenda ao gráfico, indicando que o par representa e o par representa .
Executando o programa, você terá o gráfico de e , para
Resposta
Exercício Resolvido #8
“USP – Sistemas Dinâmicos I: Usando a Ferramenta MATLAB, de Eduardo L.L. Cabral e Larissa Driemeier. Seção 9.5, exercício 4, p. 60”
A equação de movimento para um pêndulo cuja base se move horizontalmente com uma aceleração é
Suponha , e . Plote para para os seguintes casos:
- aceleração constante e ou
- aceleração linear com o tempo e
Passo 1
O enunciado nos dá uma EDO de segunda ordem representando o movimento de um pêndulo e primeiro nos pede para plotar em duas condições distintas: com constante e linear com o tempo.
Antes de tudo, precisamos converter a EDO de segunda ordem em um sistemas de EDOs de primeira ordem, pois o MATLAB só resolve EDOs de primeira ordem.
Resolveremos o sistema de EDOs a função . O enunciado nos deu todas entradas necessárias para usarmos : um intervalo de integração () e valores iniciais para e sua derivada primeira.
Na letra a do exercício, implementaremos duas vezes, uma para cada condição inicial ( ou ). Já na letra b do exercício, implementaremos somente uma vez, pois somente é dada uma condição inicial ().
Passo 2
Antes de partir para o MATLAB, temos que converter a EDO de segunda ordem para um sistema de EDOs de primeira ordem. Para isto, vamos dizer que:
Substituindo e na EDO original, temos:
Isolando na equação acima, temos:
Esta é a primeira equação do sistema de EDOs de primeira ordem.
Para construir a segunda equação do sistema, considere que:
Logo, o sistema de EDOs de primeira ordem construído a partir de é:
Usaremos esse sistema para resolver a letra a e a letra b do exercício.
Passo 3
Com o sistema de EDOs de primeira ordem, podemos partir para o MATLAB. Vamos começar respondendo a letra a, que pede para plotarmos para para aceleração constante e duas consições iniciais distintas: e . Para isto, usaremos a função do MATLAB, que tem a estrutura:
Ela tem três entradas:
- : uma função representando o sistema de EDOs de primeira ordem, no caso:
- : intervalo de integração, normalmente no formato : o intervalo começa em e termina em . Neste exercício, , , logo ;
- : vetor com as condições iniciais de e em .
Temos que e duas condições iniciais para : e . Por isso, vamos implementar 𝑜𝑑𝑒 para dois diferentes na letra a: e .
Para ambos os casos, a função nos dará duas saídas: um vetor com valores de (começando em e terminando em , correspondendo ao nosso intervalo de integração) e uma matriz de duas colunas com os valores de e (iniciando em e terminando nos valores de e correspondentes a ), representando a solução do sistema de EDOs. A primeira coluna de corresponde a , isto é, a , e a segunda coluna de corresponde a , ou seja, .
Em outras palavras, 𝑜𝑑𝑒 nos retorna os pontos que representam a função , na forma de para o intervalo de integração . Logo, é a segunda coluna de que vamos plotar.
Bora implementar tudo isso no MATLAB. Abra um script novo e crie a função , com o sistema de EDOs obtido no passo anterior:
Como queremos encontrar duas funções ( e ), a entrada da função é um vetor de dois elementos, o primeiro elemento representando e o segundo elemento, . O vetor representando as derivadas das funções e , , também é um vetor de dois elementos.
Note que a função serve para resolver a letra a do exercício, pois adotamos a aceleração constante .
Passo 4
Para resolver o sistema de EDOs para as duas condições iniciais da letra a, digite os seguintes comandos em um novo script do MATLAB:
A primeira linha cria o intervalo de integração .
As duas linhas seguintes se referem à condição inicial e as duas últimas linhas, a .
A segunda linha cria as condições iniciais de e para . Elas são representadas por um vetor de dois elementos, .
Em seguida, usamos a para resolver o sistema. Repare que no lugar de coloquei uma string . Essa string é o nome da função criada para representar o sistema de EDOs.
A saída de para será um vetor , representando a variável independente, e uma matriz com duas colunas, a primeira representando e a segunda, . A saída representa a solução do sistema de EDOs para .
De maneira similar, a quarta linha cria as condições iniciais de e para , indicadas por .
A linha seguinte usa para resolver o sistema para . As saídas serão um vetor e uma matriz de duas colunas, a primeira representando e a segunda, . A saída representa a solução do sistema de EDOs para .
Passo 5
Após obtermos a solução do sistema EDOs para ambas as condiçõe inicias da letra a, podemos gerar as curvas de para ambos os casos, usando as saídas de . A 𝑜𝑑𝑒45 nos retorna os pontos que representam na primeira coluna de e e os pontos que representam na segunda coluna de e . Sabendo que e é que o exercício nos pede para plotar, são as segundas colunas de e que usaremos para plotar o gráfico.
Para plotar para uma acelerção constante com as duas condições iniciais distintas, entre os seguintes comandos no script onde você usou a função :
Na primeira linha, pedimos ao MATLAB para gerar um figura com o comando . Esta figura terá o gráfico de da letra a do exercício. Usamos esse comando para que os gráficos da letra a e b seja plotados em janelas diferentes.
Na segunda linha, usamos a função para gerar, em um mesmo gráfico, as curvas de para e . O primeiro par se refere a e pega a segunda coluna de , correspondendo a , e a plota em função de . Da mesma maneira, o segundo par é referente a e pega a segunda coluna de , também correspondendo a , e a plota em função de .
Na terceira linha, acrescentamos uma legenda ao gráfico, indicando que o par se refere a a e o par se refere a a .
Para obter o gráfico da letra a, rode o programa:
Passo 6
A letra b pede para plotar considerando uma aceleração linear com o tempo e . Para isto, também usaremos a função para resolver o sistema de EDOs de primeira ordem do passo 2, mas devemos montar uma nova função com o sistema de EDOs, considerando que varia com o tempo. Por isso, em um novo script, copie e cole a função criada no passo 3, alterando a variável para :
Chamei essa nova função de . Ele tem exatamente a mesma forma da anterior, a única diferença é que a variável não é mais constante.
Após salvar a função , no mesmo script onde você resolveu a letra a do exercício, implemente mais uma vez, mas para :
A primeira linha cria as condições iniciais de e para . Elas são representadas por um vetor de dois elementos, .
Em seguida, usamos a para resolver o sistema. Repare que no lugar de coloquei uma string , para resolver o sistema de EDOS com as condições da letra b. A saída de para a letra b do exercício será o vetor , representando a variável independente, e a matriz de duas colunas , a primeira representando e a segunda, .
Como , é a segunda coluna de que vamos plotar.
Passo 7
Para plotar para a letra b do exercício, adicione em seu script os comandos abaixo:
Na primeira linha, pedimos ao MATLAB para criar uma segunda figura, com o comando . Desta forma, teremos os gráficos da letra a e da letra b em janelas diferentes.
Na segunda linha, usamos o comando para plotar com aceleração linear com o tempo. Para isto, plotamos o par , que plota a segunda coluna de em função de .
Rode o programa e você terá o gráfico da solução da letra b do exercício.
Resposta
Ei, a resposta está no passo a passo :)