Exercícios de Equações Diferenciais Ordinárias (EDO) - Lista de Exercícios Resolvida

A equação de movimento para um pêndulo cuja base se move horizontalmente com uma aceleração é

Suponha , e . Plote para para os seguintes casos:

1. aceleração constante e ou
2. aceleração linear com o tempo e

Considere o sistema de equações diferenciais de primeira ordem com condições iniciais, dado por

Este sistema modela a interação entre duas populações, uma de presas e outra de predadores. Faça o gráfico de e , para

Considere o reator bioquímico descrito na figura abaixo, onde representa a biomassa presente no reator e o substrato. O reator possui um volume constante () uma vez que as vazões de alimentação e de saída são iguais (). A corrente de alimentação possui concentração de substrato igual a x2i e uma concentração de biomassa igual a zero.

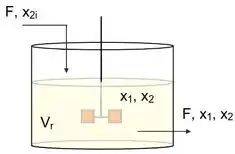
Bequette (1998) propõe o modelo descrito pela equação abaixo para o processo:

onde é a relação constante entre as taxas de geração de biomassa e o consumo de substrato e é o coeficiente de taxa de crescimento descrito pela equação:

Descreva o comportamento das concentrações de biomassa e de substrato considerando um tempo de integração de 30 horas (), as condições iniciais:

E os valores para os parâmetros descritos na tabela abaixo:

BEQUETTE, B. W., Process Dynamics: Modeling, Analysis and Simulation, 1a ed. USA, PrenticeHall PTR, 1998.

Dado o Problema de Valor Inicial (PVI) abaixo:

, ,

1. Reescreva o PVI como um sistema de equações diferenciais de primeira ordem;
2. Resolva o sistema de EDO e plote a função e sua primeira derivada.

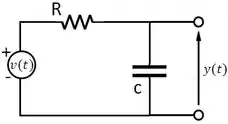
O modelo do circuito RC mostrado na figura abaixo pode ser encontrado a partir da lei das tensões de Kirchhoff e da conservação da carga:

Suponha que o valor de seja . Utilize um método numérico para encontrar a resposta para o caso em que a tensão externa aplicada é zero e que a tensão inicial do capacitor seja . Compare os resultados com a solução analítica, que é

Uma avançada turbina chamada de ventilador não canalizado (UDF) é uma das novas tecnologias mais promissoras que tem sido desenvolvida para o futuro transporte de aeronaves.

Turbinas, que têm sido usadas por décadas, combinam o poder e a confiabilidade dos motores a jato com a eficiência dos propulsores. Eles constituem uma importante melhoria dos antigos propulsores movidos a pistão. Suas aplicações têm sido limitadas a pequenas aeronaves do tipo comutador, isto porque eles não são tão rápidos, nem poderosos quanto as turbinas usadas em grandes aeronaves. Esse tipo de turbina (UDF) implica em avanços significantes na tecnologia de propulsão. Novos materiais, aerodinâmica e velocidades de alta rotação habilitam esta turbina a voar tão rápido quanto as turbinas a jato, e com grande aproveitamento de combustível. A UDF é também menos barulhenta que o sistema convencional de turbinas.

Durante um teste de vôo de uma turbina UDF de uma aeronave, o motor é levado para um nível de , o que significa os da aeronave tendo alcançado uma velocidade de . As válvulas de regulação do motor são então levadas para atingir um nível de , e a aeronave começa a acelerar.

A equação diferencial que determina a aceleração da aeronave é:

Onde:

nível atingido em

massa em

velocidade em

Escreva no MATLAB um programa para determinar a nova velocidade depois de uma mudança no nível do motor através do gráfico da solução para a equação diferencial. Considere um intervalo de tempo de 6 min.

Seja a equação:

1. Assumindo como condição inicial , resolva, no MATLAB, essa equação diferencial no intervalo de e plote o gráfico com os valores correspondentes de .
2. Sendo a solução analítica para esta equação, faça um novo gráfico que compare a solução analítica com a numérica.

Utilize um método de Runge-Kutta explícito para aproximar , sabendo que