Transformada de Fourier

Teoria

Introdução

E aí, meu povo, tudo joia? Deixa eu te perguntar: você curte música? Não importa o gênero: sertanejo, axé, pagode ou samba, todo mundo ama uma musiquinha. Já parou pra pensar como as gravadoras fazem o tratamento do som gravado após sua banda favorita terminar as gravações no estúdio? Não?

Pois saiba que eles usam um conceito que a gente usa muito em engenharia, especialmente em tratamento de sinais. Eles usam a transformada de Fourier, que decompõe um sinal em senos e cossenos, para converter um sinal no domínio do tempo, como por exemplo o canto do vocalista ou um solo maneiro de guitarra, para o domínio da frequência.

O domínio do tempo, que pode ser dado em segundos, por exemplo, é representado por valores reais. Já o domínio da frequência é representado por valores complexos, que, por sua vez, podem ser representados por senoides que compõem o sinal.

E por que eles fazem isso? Porque às vezes pode ser muito mais fácil analisar um sinal no domínio da frequência do que no domínio do tempo. A transformada de Fourier é muito utilizada no tratamento de sinais de diversas áreas do conhecimento. Ela pode ser usada para resolver problemas de condução térmica, interpretar eletrocardiogramas, eletroencefalogramas e sinais de pressão sanguínea e até mesmo para estudar terremotos!

A função do MATLAB fft

O MATLAB tem uma função chamada que calcula a transformada de Fourier de um vetor , o qual está no domínio do tempo:

A saída é um vetor com números complexos: é a conversão de no domínio do tempo para o domínio da frequência.

O vetor pode ser alguma medição que fazemos no domínio do tempo, como a gravação de um instrumento, por exemplo. A assume que os elementos do vetor tem um passo constante (por exemplo, tem passo constante igual a ) e o vetor de saída tem a mesma quantidade de elementos de .

Veja que o uso da função é bem direto. Porém, antes de vermos um exemplo de aplicação da , para entendermos bem como utilizá-lo, precisamos ver bem direitinho o que é esse negócio de “domínio do tempo” e “domínio da frequência”.

Domínio do Tempo versus Domínio da Frequência

No mundo real, trabalhamos com sinais analógicos, que são funções contínuas no tempo, como no caso da gravação de um solo de guitarra. Para que este sinal contínuo seja processado por um computador, ele deve ser amostrado em um período de segundos, gerando assim um sinal digital derivado do sinal analógico original.

Digamos que você fez uma captura de sinal com pontos de medição, registrados a cada . Normalmente se começa a amostragem em , logo, este seria o domínio do tempo para esta medição:

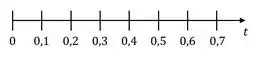
Neste caso, o período é .

Lembra láááá das aulas de ondulatória de Física, que a frequência é o inverso do período? Em outras palavras:

Podemos dizer então que a frequência de amostragem da nossa medição é igual a:

O domínio da frequência normalmente também se inicia em e as frequências seguintes são obtidas somando um constante a elas, definido por:

Onde é a frequência de amostragem e o número de pontos dos dados originais. Na nossa medição, temos .

Para nosso exemplo, tendo e , o domínio da frequência seria igual a:

O domínio da frequência gerado por corresponde a uma frequência com separação de

Existe um teorema chamado de teorema de amostragem de Nyquist, que diz que a frequência de amostragem deve ser maior que o dobro da frequência máxima do sinal no domínio do tempo. Desta forma, o sinal digital é mais fiel ao sinal analógico.

Por exemplo, no nosso exemplo, como nossa frequência de amostragem é , o ideal é que o sinal medido tenha uma frequência de até .

É importante entender bem como se determina o domínio da frequência para poder trabalhar com a saída da função . A função do MATLAB é válida para um intervalo no domínio da frequência que vai de . A partir de , os resultados da se repetem.

Exemplo no MATLAB

Agora que conhecemos como funciona esse negócio de domínio do tempo e domínio da frequência, vamos ver como usamos a no MATLAB.

Digamos que você registrou uma onda senoidal fazendo medições a cada . Essa onda tem uma amplitude e uma frequência de . Ela pode ser descrita pela seguinte expressão:

onde é o tempo de medição do sinal, que pode ser calculado a partir do período .

Ah, não confunda a frequência da onda senoidal () com a frequência de amostragem ou com o . Apesar de se tratarem de frequências, elas representam coisas diferentes: usamos e para construir o dommínio da frequência, já a frequência da onda senoidal representa o número de oscilações dela, por um certo período de tempo.

Vamos construir essa onda senoidal no MATLAB para vermos a carinha dela? Em um script novo, entre as linhas de código:

Com estes comandos, entramos com o número de pontos medidos , o período , a amplitude e a frequência da onda senoidal .

Para criar a onda senoidal, devemos criar um vetor representando o tempo em segundos. Ele é criada a partir do período , com o comando:

Com este comando, cria-se primeiro um vetor que vai de a , com passo de (). Este vetor tem elementos, correspondendo aos pontos de medição. Lembra que esses pontos foram registrados a cada ? Por isso, esse vetor é multiplicado por . Desta forma, é criado o domínio do tempo, que vai de a .

Após entrar as informações da onda senoidal, vamos entrar com a sua expressão no script:

Ali já pedimos também pro MATLAB plotar esta curva senoidal no domínio do tempo, usando . Indicamos que o eixo horizontal do gráfico está no domínio do tempo com o comando . Rodando o código, vemos que ela tem essa carinha:

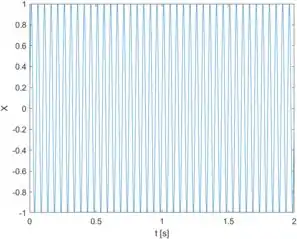
Vamos ver essa onda no domínio da frequência. Digite no seu código a função :

Ela terá como entrada o vetor , que corresponde à nossa onda senoidal no domínio do tempo, e retornará um vetor da onda senoidal no domínio da frequência.

Como dissemos acima, a saída de é um vetor cujos elementos são números complexos, no formato:

Onde é a componente real e , a imaginária. A representação de um sinal no domínio da frequência, o vetor , carrega a informação da magnitude do sinal em cada frequência.

A magnitude do sinal é dada pela magnitude do número complexo, que á calculada como:

Vamos aplicar esse conceito na nossa saída de . No nosso script, entre a linha de código:

Com esta linha, calculamos a magnitude de cada elemento do vetor usando a função do MATLAB. Quando a entrada da função é um número complexo, ela calcula sua magnitude.

É interessante gerarmos o gráfico de para vermos como ele ficou. Vamos gerar esse gráfico no domínio da frequência. Para criar o eixo horizontal do gráfico, entre com as linhas de código:

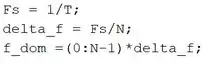
Na primeira linha, calculamos a frequência de amostragem , que vimos lá em cima.

Na segunda linha, calculamos o , que também vimos lá em cima. O é armazenado na variável .

Na terceira linha, geramos o domínio da frequência, representado pelo vetor . A lógica da sua criação é igualzinha à lógica que usamos para criar o vetor , do domínio do tempo.

Primeiramente, cria-se um vetor que vai de a , com passo de (). Este vetor tem elementos, correspondendo aos pontos de medição. Em seguida, esse vetor é multiplicado por . Desta forma, é criado o domínio da frequência, que vai de a

Tendo criado o domínio da frequência, vamos usar novamente a função para gerar o gráfico:

Pedimos ao MATLAB para gerar uma segunda figura com o comando , para termos o gráfico no domínio da frequência em uma janela diferente do gráfico no domínio do tempo.

Em seguida, com o comando o gráfico da magnitude de , no domínio da frequência, é efetivamente gerado. Repare que, para plotar, usamos somente a primeira metade dos vetores com elementos e . Isso é indicado pela adição de à direita do nome do vetor, que diz ao MATLAB que queremos pegar do primeiro elemento ao elemento do vetor.

Usamos somente a primeira metade dos vetores e porque, no domínio da frequência, a partir de , as magnitudes começam a se repetir e não precisamos pôr elas no gráfico para fazermos a análise dos resultados.

Indicamos que o eixo horizontal do gráfico é o domínio da frequência por meio do comando . Temos no eixo vertical do gráfico a magnitude de , indicado por .

Ao rodarmos o programa, geramos este segundo gráfico:

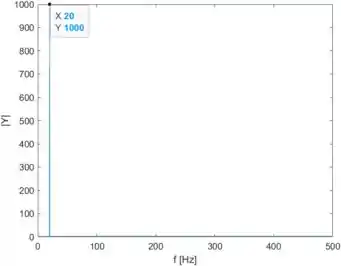
No gráfico, já marquei ali o ponto do pico de magnitude, para ver as coordenadas dele. Veja que ele ocorre em uma frequência igual a , exatamente a mesma frequência da onda senoidal. Isso ocorre pois usamos frequência de amostragem maior que o dobro da frequência da onda. Se você olhar a variável , representando a frequência amostral, verá que , muito maior que o dobro da frequência de da onda senoidal.

Caso usássemos uma frequência de amostragem menor ou igual a , não obedeceríamos ao teorema de Nyquist e não veríamos esse comportamento.

Aplicamos o conceito de magnitude no vetor dado por para estudarmos o comportamento do sinal. No exemplo da onda senoidal, vemos pelo gráfico da magnitude de que o sinal é periódico.

“Tá, mas já dava pra ver isso no domínio do tempo da onda senoidal”, você deve estar pensando. Por se tratar de uma onda simples e bem conhecida, realmente, poderíamos já ver lá. Mas tem casos em que os sinais são bem mais complexos e precisamos fazer essa análise da magnitude no domínio da frequência para identificar algum comportamento. É o caso, por exemplo, da análise de vibrações de um prédio durante um terremoto.

E aí, curtiu a aula? É um assunto bem complexo, por isso é bom praticar bastante. Bora fazer os exercícios ;D

Domínio do Tempo versus Domínio da Frequência

Exemplo no MATLAB

Exercícios Resolvidos

Exercício Resolvido #1

“UnB - Laboratório 08: A Transformada Rápida de Fourier (FFT) e análise espectral”

Trace um sinal senoidal com as propriedades a seguir:

Amplitude:
Frequência:
Fase inicial:
Número total de pontos de dados:
Tempo de duração: - segundo

Verifique se o método FFT dá a mesma frequência .

Passo 1

O exercício nos dá algumas propriedades de uma onda senoidal, no domínio do tempo, e nos pede para aplicar a transformada de Fourier nela. Para isto, usaremos a função do MATLAB.

Para verificar se “o método FFT dá a mesma frequência ”, geraremos um gráfico da magnitude da onda senoidal no domínio da frequência, após a aplicação da função , e veremos as coordenadas do primeiro pico de magnitude. O pico de magnitude deve ocorrer na frequência da onda senoidal.

Passo 2

Primeiramente, vamos criar a onda senoidal no MATLAB. Em um novo script, vamos entrar as propriedades de amplitude, frequência, fase inicial e número de pontos:

A amplitude da onda senoidal é armazenada na variável , a frequência em , a fase inicial em e o número de pontos em .

Vamos criar agora o vetor representando o intervalo de a de duração da onda. Para criar o vetor , usaremos o comando:

Neste comando, cria-se primeiro um vetor que vai de a , com passo de (). Este vetor tem elementos, correspondendo aos pontos de dados. Em seguida, esse vetor é multiplicado por , que é o período, em segundos, da onda senoidal.

O enunciado não nos dá o período, mas sabemos que a onda tem um intervalo de duração de a . Logo, o vetor deve começar em e terminar em . O último elemento de deve ser igual a:

Sabemos que , logo o período é igual a:

Vamos entrar essa informação no MATLAB e construir o vetor :

O vetor representa o domínio do tempo da onda senoidal.

Temos todos os dados necessários para construir a onda senoidal no domínio do tempo. No MATLAB, digite este comando para gerar a onda:

A onda senoidal é representada pelo vetor . Vamos ver a carinha dela? Digite as linhas de código abaixo no seu script para plotar o gráfico da onda senoidal no domínio do tempo:

Na primeira linha, pedimos ao MATLAB para gerar uma figura com o comando , para termos o gráfico no domínio do tempo em uma janela diferente do gráfico no domínio da frequência (que geraremos mais pra frente, no mesmo script).

Em seguida, com o comando o gráfico da onda senoidal, no domínio do tempo, é efetivamente gerado.

Indicamos que o eixo horizontal do gráfico é o domínio do tempo por meio do comando . Temos no eixo vertical do gráfico os valores da onda senoidal, indicados por .

Ao rodarmos o programa, vemos como é a onda senoidal:

Passo 3

Vamos agora calcular a onda senoidal no domínio da frequência. Para isto, usaremos a função do MATLAB, que tem a seguinte estrutura:

A entrada da função é um vetor contendo dados no domínio do tempo, representados por numeros reais. Já a saída é um vetor com números complexos: é a conversão de no domínio do tempo para o domínio da frequência. Os vetores e têm a mesma quantidade de elementos.

Digite no seu script o comando:

Com esta linha de código, o MATLAB passará a onda senoidal, que está no domínio do tempo e é representada pelo vetor , para o domínio da frequência. A onda senoidal no domínio da frequência é representada pelo vetor .

Para verificarmos se o método FFT dá a mesma frequência de , precisamos gerar o gráfico da magnitude da onda senoidal no domínio da frequência.

Passo 4

Para construirmos o gráfico da magnitude da onda senoidal no domínio da frequência, vamos calcular a magnitude usando a função do MATLAB. Digite no MATLAB a linha de código:

Com esta linha, calculamos a magnitude de cada elemento do vetor usando a função do MATLAB. Quando a entrada da função é um número complexo, ela calcula sua magnitude.

Com esse comando, já temos o eixo vertical do gráfico, agora precisamos criar o eixo horizontal, representando o domínio da frequência. Para isto, digite os comandos:

Na primeira linha, calculamos a frequência de amostragem , que é o inverso do período .

Na segunda linha, calculamos o , que é o passo do domínio da frequência: ele começa em e as frequências seguintes são obtidas pela soma de à frequência anterior. O é calculado dividindo a frequência de amostragem pelo número de pontos e é armazenado na variável .

Na terceira linha, geramos o domínio da frequência, representado pelo vetor . A lógica da sua criação é igualzinha à lógica que usamos para criar o vetor , do domínio do tempo.

Primeiramente, cria-se um vetor que vai de a , com passo de (). Este vetor tem elementos, correspondendo aos pontos de dados. Em seguida, esse vetor é multiplicado por . Desta forma, é criado o domínio da frequência, que vai de a

Após criar o domínio da frequência, vamos usar novamente a função para gerar o gráfico da magnitude da onda senoidal no domínio da frequência:

Na primeira linha, pedimos ao MATLAB para gerar uma segunda figura com o comando , para termos o gráfico no domínio da frequência em uma janela diferente do gráfico no domínio do tempo.

Em seguida, o gráfico da magnitude de no domínio da frequência é criado com o comando Repare que, para plotar, usamos somente a primeira metade dos vetores com elementos e . Isso é indicado pela adição de à direita do nome do vetor, que diz ao MATLAB que queremos pegar do primeiro elemento ao elemento do vetor.

Usamos somente a primeira metade dos vetores e porque, no domínio da frequência, a partir de , as magnitudes começam a se repetir e não precisamos pôr elas no gráfico para encontrar o que o exercício pede.

Indicamos que o eixo horizontal do gráfico é o domínio da frequência por meio do comando . Temos no eixo vertical do gráfico a magnitude de , indicado por .

Passo 5

Vamos rodar o programa para ver o gráfico da magnitude da onda senoidal no domínio da frequência:

Já marquei no gráfico as coordenadas do pico de magnitude da onda senoidal no domínio da frequência. Ele ocorre em uma frequência de , muito próxima da frequência da onda senoidal, que é de . Logo, podemos dizer que o método FFT dá a mesma frequência .

Dica: caso aumentássemos o número de pontos , teríamos uma maior precisão e a frequência onde ocorre o pico de magnitude seria mais próxima de .

Resposta

O método FFT dá a mesma frequência da onda senoidal, pois o pico de magnitude ocorre em uma frequência de , muito próxima de .

Exercício Resolvido #2

“Adaptado de UERJ, Curso de MATLAB 5.1: Introdução à Solução de Problemas de Engenharia, Laboratório de Engenharia Elétrica, p. 148”

Gere 128 pontos para o seguinte sinal:

Plote o sinal no domínio do tempo. Usando o método da transformada de Fourier, gere e plote o sinal no domínio da freqüência. Use a escala de no eixo X. Assuma a taxa de amostragem de . Verifique se os picos ocorrem onde era esperado para o domínio da freqüência.

Passo 1

O enunciado nos dá uma função representando um sinal no domínio do tempo e nos pede para:

Plotar o sinal no domínio do tempo;
Aplicar a transformada de Fourier no sinal para obtê-lo no domínio da frequência. Para isto, usaremos a função do MATLAB;
Plotar o sinal do domínio da frequência, tendo as frequências em no eixo X do gráfico;
Verificar se os picos do sinal ocorrem onde era esperado no domínio da frequência.

A partir do enunciado e da equação do sinal, que é uma onda senoidal, podemos obter algumas informações para entrarmos no MATLAB e resolvermos o exercício:

O número de pontos que o sinal deve ter é ;
A taxa de amostragem é de . Isto quer dizer que a frequência de amostragem é ;
A partir da frequência de amostragem, obtemos o período em segundos do sinal: ;
Uma onda senoidal normalmente tem o formato:

Onde é a amplitude da onda e , a frequência em .

Logo, podemos dizer que a amplitude do sinal é de ;
E que a frequência do sinal é de .

Para verificar se os picos do sinal ocorrem onde era esperado no domínio da frequência, devemos olhar o gráfico do sinal no domínio da frequência e ver se o pico ocorre na mesma frequência do sinal: .

Passo 2

Primeiramente, vamos entrar no MATLAB as informações fornecidas pelo enunciado, que foram listadas logo acima, no passo 1. Em um script novo, digite:

O número de pontos é armazenado na variável ; a frequência de amostragem na variável ; o período é calculado e armazenado na variável ; a amplitude da onda senoidal é armazenada na variável ; e, finalmente, a frequência do sinal é armazenada em .

Para fazermos a primeira coisa que o exercício pede – plotar o sinal no domínio do tempo – devemos criar um vetor representando o domínio do tempo a partir o comando:

Neste comando, cria-se primeiro um vetor que vai de a , com passo de (). Este vetor tem elementos, correspondendo aos pontos pedidos pelo enunciado. Em seguida, esse vetor é multiplicado por , que é o período, em segundos, da onda senoidal.

Vamos acrescentar esse comando para calcular o vetor no MATLAB e aproveitar e já gerar o sinal no domínio do tempo:

Tendo os vetores e , podemos plotar o sinal da onda senoidal no domínio do tempo, por meio dos comandos:

Na primeira linha, pedimos ao MATLAB para gerar uma figura com o comando , para termos o gráfico no domínio do tempo em uma janela diferente do gráfico no domínio da frequência (que também foi pedido no exercício e que geraremos mais pra frente, no mesmo script).

Em seguida, com o comando o gráfico do sinal no domínio do tempo é gerado.

Indicamos que o eixo horizontal do gráfico é o domínio do tempo por meio do comando . Temos no eixo vertical do gráfico os valores da onda senoidal, indicado por .

Vamos ver a carinha do sinal no domínio do tempo? Rodando o programa que escrevemos até agora, temos este gráfico:

Pronto! O primeiro item pedido pelo exercício está feito!

Passo 3

A segunda coisa que o exercício pede é usarmos a transformada de Fourier no sinal para obtermos a onda senoidal no domínio da frequência. Para isto, usaremos a função do MATLAB, incluindo a seguinte linha de código em nosso script:

Para calcular a transformada de Fourier, a função tem como entrada o vetor , que contém números reais representando o sinal no domínio do tempo. Já a saída é um vetor com números complexos: é a conversão de no domínio do tempo para o domínio da frequência. Os vetores e têm a mesma quantidade de elementos.

O segundo item pedido pelo exercício está feito (esse foi bem diretão XD)

Passo 4

Tendo executado o segundo item pedido pelo exercício, partimos para a terceira coisa que ele nos pede para fazer: plotar o sinal no domínio da frequência. Quando plotamos um sinal no domínio da frequência, normalmente temos no eixo Y do gráfico a magnitude do sinal obtido pela função . Para calcular a magnitude, usamos a função do MATLAB. Digite no MATLAB a linha de código:

Com esta linha, calculamos a magnitude de cada elemento do vetor usando a função do MATLAB. Quando a entrada da função é um número complexo, ela calcula sua magnitude.

Agora precisamos criar o eixo horizontal, representando o domínio da frequência. Para isto, digite os comandos:

Na primeira linha, calculamos o , que é o passo do domínio da frequência: ele começa em e as frequências seguintes são obtidas pela soma de à frequência anterior. O é calculado dividindo a frequência de amostragem pelo número de pontos e é armazenado na variável .

Na segunda linha, geramos o domínio da frequência, representado pelo vetor . A lógica da sua criação é igualzinha à lógica que usamos para criar o vetor , do domínio do tempo.

Primeiramente, cria-se um vetor que vai de a , com passo de (). Este vetor tem elementos, correspondendo aos pontos exigidos pelo enunciado. Em seguida, esse vetor é multiplicado por . Desta forma, é criado o domínio da frequência, que vai de a

Após criar o domínio da frequência, vamos usar novamente a função para gerar o gráfico da magnitude da onda senoidal no domínio da frequência:

Na primeira linha, pedimos ao MATLAB para gerar uma segunda figura com o comando , para termos o gráfico no domínio da frequência em uma janela diferente do gráfico no domínio do tempo.

Indicamos que o eixo horizontal do gráfico é o domínio da frequência por meio do comando . Temos no eixo vertical do gráfico a magnitude de , indicado por .

Vamos ver a cara do sinal do domínio da frequência? Executando o programa, temos:

Voilà! Terceiro item pedido pelo exercício feito ;D

Passo 5

A última coisa que o exercício pede para fazermos é verificar se os picos do sinal ocorrem onde era esperado no domínio da frequência. Para vermos isso, devemos olhar o gráfico do sinal no domínio da frequência e ver se o pico ocorre na mesma frequência do sinal: .

Vamos clicar no pico do gráfico gerado para ver suas coordenadas:

O pico ocorre em , que está bem próximo de . Logo, o pico do sinal ocorre onde era esperado.

Se quiser, faça alguns testes aumentando o , você verá que a frequência onde ocorre o pico ficará mais próxima de , até se tornar igual a .

Resposta

Gráfico do sinal no domínio do tempo:

Gráfico do sinal do domínio da frequência, tendo as frequências em no eixo X:

O pico do sinal ocorre onde era esperado no domínio da frequência: próximo de , que é a frequência do sinal .

Exercício Resolvido #3

“Adaptado de UERJ, Curso de MATLAB 5.1: Introdução à Solução de Problemas de Engenharia, Laboratório de Engenharia Elétrica, p. 148”

Gere 128 pontos para o seguinte sinal:

Plote o sinal no domínio do tempo. Usando o método da transformada de Fourier e gere e plote o sinal no domínio da frequência. Use a escala de no eixo X. Assuma a taxa de amostragem de . Verifique se os picos ocorrem onde era esperado para o domínio da frequência.

Passo 1

O enunciado nos dá uma função representando um sinal no domínio do tempo e nos pede para:

Plotar o sinal no domínio do tempo;
Aplicar a transformada de Fourier no sinal para obtê-lo no domínio da frequência. Para isto, usaremos a função do MATLAB;
Plotar o sinal do domínio da frequência, tendo as frequências em no eixo X do gráfico;
Verificar se os picos do sinal ocorrem onde era esperado no domínio da frequência.

A partir do enunciado e da equação do sinal, que é composta por ondas cossenodal e seinodal, podemos obter algumas informações para entrarmos no MATLAB e resolvermos o exercício:

O número de pontos que o sinal deve ter é ;
A taxa de amostragem é de . Isto quer dizer que a frequência de amostragem é ;
A partir da frequência de amostragem, obtemos o período em segundos do sinal: ;
Chamando de:

Temos:

Uma onda cossenoidal normalmente tem o formato:

Onde é a amplitude da onda e , a frequência em .

Logo, podemos dizer que a amplitude de é de ;
Já a frequência de é:

Uma onda senoidal normalmente tem o formato:

Logo, podemos dizer que a amplitude de é de ;
E que a frequência de é:

Para verificar se os picos do sinal ocorrem onde era esperado no domínio da frequência, devemos olhar o gráfico do sinal no domínio da frequência e ver se os picos ocorrem na mesma frequência das ondas que compõem o sinal: e .

Passo 2

Primeiramente, vamos entrar no MATLAB as informações fornecidas pelo enunciado, que foram listadas logo acima, no passo 1. Em um script novo, digite:

O número de pontos é armazenado na variável ; a frequência de amostragem na variável ; o período é calculado e armazenado na variável ; a amplitude da onda é armazenada na variável e amplitude da onda , na variável ; e, finalmente, a frequência de em é armazenada em e a frequência de , em .

Para fazermos a primeira coisa que o exercício pede – plotar o sinal no domínio do tempo – devemos criar um vetor representando o domínio do tempo a partir o comando:

Vamos acrescentar esse comando para calcular o vetor no MATLAB e aproveitar e já gerar o sinal no domínio do tempo:

Nos comandos acima, após criar o vetor , criamos um vetor chamado representando a onda cosseinodal e outro vetor chamado representando a onda senoidal .

O sinal é criado em seguida, fazendo .

Tendo os vetores e , podemos plotar o sinal no domínio do tempo, por meio dos comandos:

Em seguida, com o comando o gráfico do sinal no domínio do tempo é gerado.

Indicamos que o eixo horizontal do gráfico é o domínio do tempo por meio do comando . Temos no eixo vertical do gráfico o sinal , indicado por .

Vamos ver a carinha do sinal no domínio do tempo? Rodando o programa que escrevemos até agora, temos este gráfico:

Pronto! O primeiro item pedido pelo exercício está feito!

Passo 3

A segunda coisa que o exercício pede é usarmos a transformada de Fourier no sinal para obtermos a onda no domínio da frequência. Para isto, usaremos a função do MATLAB, incluindo a seguinte linha de código em nosso script:

Ao incluirmos esse comando no nosso código, o segundo item pedido pelo enunciado está feito (sim, esse passo foi bem curto XD)

Passo 4

Com esta linha, calculamos a magnitude de cada elemento do vetor usando a função do MATLAB. Quando a entrada da função é um número complexo, ela calcula sua magnitude.

Agora precisamos criar o eixo horizontal, representando o domínio da frequência. Para isto, digite os comandos:

Na segunda linha, geramos o domínio da frequência, representado pelo vetor . A lógica da sua criação é igualzinha à lógica que usamos para criar o vetor , do domínio do tempo.

Após criar o domínio da frequência, vamos usar novamente a função para gerar o gráfico da magnitude da onda no domínio da frequência:

Na primeira linha, pedimos ao MATLAB para gerar uma segunda figura com o comando , para termos o gráfico no domínio da frequência em uma janela diferente do gráfico no domínio do tempo.

Indicamos que o eixo horizontal do gráfico é o domínio da frequência por meio do comando . Temos no eixo vertical do gráfico a magnitude de , indicado por .

Vamos ver a cara do sinal do domínio da frequência? Executando o programa, temos:

Voilà! Terceiro item pedido pelo exercício feito ;D

Passo 5

Vamos clicar em cima dos picos no gráfico gerado do MATLAB, para vermos suas coordenadas. Vamos clicar no primeiro pico, mais à esquerda:

Viu que ele ocorre em ? Bem próximo da frequência de , que é .

Clicando no segundo pico, mais à direita:

Ele ocorre exatamente em , mesma frequência de .

Portanto, os picos do sinal no domínio da frequência ocorrem onde eram esperados.

Se quiser, faça alguns testes aumentando o , você verá que as frequências onde ocorrem os picos ficarão mais próximas de e , até se tornarem iguais a e .

Resposta

Gráfico do sinal no domínio do tempo:

Gráfico do sinal do domínio da frequência, tendo as frequências em no eixo X:

Os picos do sinal no domínio da frequência ocorrem onde eram esperados: nas frequências de e , correspondendo às frequências das ondas que compõem o sinal .

Exercício Resolvido #4

“Adaptado de UERJ, Curso de MATLAB 5.1: Introdução à Solução de Problemas de Engenharia, Laboratório de Engenharia Elétrica, p. 148”

Gere 128 pontos para o seguinte sinal:

Plote o sinal no domínio do tempo. Usando o método da transformada de Fourier e gere e plote o sinal no domínio da freqüência. Use a escala de no eixo X. Assuma a taxa de amostragem de . Verifique se os picos ocorrem onde era esperado para o domínio da freqüência.

Passo 1

O enunciado nos dá uma função representando um sinal no domínio do tempo e nos pede para:

Plotar o sinal no domínio do tempo;
Aplicar a transformada de Fourier no sinal para obtê-lo no domínio da frequência. Para isto, usaremos a função do MATLAB;
Plotar o sinal do domínio da frequência, tendo as frequências em no eixo X do gráfico;
Verificar se os picos do sinal ocorrem onde era esperado no domínio da frequência.

A partir do enunciado e da equação do sinal, que é uma onda cossenoidal, podemos obter algumas informações para entrarmos no MATLAB e resolvermos o exercício:

O número de pontos que o sinal deve ter é ;
A taxa de amostragem é de . Isto quer dizer que a frequência de amostragem é ;
A partir da frequência de amostragem, obtemos o período em segundos do sinal: ;
Uma onda cossenoidal normalmente tem o formato:

Onde é a amplitude da onda e , a frequência em .

Logo, podemos dizer que a amplitude do sinal é de ;
E que a frequência do sinal é:

Passo 2

Primeiramente, vamos entrar no MATLAB as informações fornecidas pelo enunciado, que foram listadas logo acima, no passo 1. Em um script novo, digite:

O número de pontos é armazenado na variável ; a frequência de amostragem na variável ; o período é calculado e armazenado na variável ; e a amplitude da onda cossenoidal é armazenada na variável .

Para fazermos a primeira coisa que o exercício pede – plotar o sinal no domínio do tempo – devemos criar um vetor representando o domínio do tempo a partir o comando:

Vamos acrescentar esse comando para calcular o vetor no MATLAB e aproveitar e já gerar o sinal no domínio do tempo:

Tendo os vetores e , podemos plotar o sinal da onda cossenoidal no domínio do tempo, por meio dos comandos:

Em seguida, com o comando o gráfico do sinal no domínio do tempo é gerado.

Indicamos que o eixo horizontal do gráfico é o domínio do tempo por meio do comando . Temos no eixo vertical do gráfico os valores da onda cossenoidal, indicado por .

Vamos ver a carinha do sinal no domínio do tempo? Rodando o programa que escrevemos até agora, temos este gráfico:

Tcharam! Primeiro ponto pedido pelo exercício resolvido.

Passo 3

A segunda coisa que o exercício pede é usarmos a transformada de Fourier no sinal para obtermos a onda cossenoidal no domínio da frequência. Para isto, usaremos a função do MATLAB, incluindo a seguinte linha de código em nosso script:

Pronto! Segundo pedido do exercício atendido ;D

Passo 4

Com esta linha, calculamos a magnitude de cada elemento do vetor usando a função do MATLAB. Quando a entrada da função é um número complexo, ela calcula sua magnitude.

Agora precisamos criar o eixo horizontal, representando o domínio da frequência. Para isto, digite os comandos:

Na segunda linha, geramos o domínio da frequência, representado pelo vetor . A lógica da sua criação é igualzinha à lógica que usamos para criar o vetor , do domínio do tempo.

Após criar o domínio da frequência, vamos usar novamente a função para gerar o gráfico da magnitude da onda cossenoidal no domínio da frequência:

Na primeira linha, pedimos ao MATLAB para gerar uma segunda figura com o comando , para termos o gráfico no domínio da frequência em uma janela diferente do gráfico no domínio do tempo.

Indicamos que o eixo horizontal do gráfico é o domínio da frequência por meio do comando . Temos no eixo vertical do gráfico a magnitude de , indicado por .

Vamos ver como o sinal ficou no domínio da frequência? Ao rodar o programa, temos o seguinte gráfico:

Terceiro item do exercício feito ;) Bora encerrar respondendo à última coisa pedida pelo exercício.

Passo 5

“Ué, mas o gráfico tem dois picos”, você deve ter reparado. Vamos ver as coordenadas dos dois, clicando neles no gráfico:

Vamos analisar primeiro o pico mais à direita, que ocorre a uma frequência de , muito próxima dos da função cosseno do sinal . Logo, este pico ocorre onde era esperado.

Se quiser, faça alguns testes aumentando o , você verá que a frequência onde ocorre o pico mais à direita ficará mais próxima de .

Você deve estar estranhando o primeiro pico, que ocorre a uma frequência de . Vamos rever o sinal :

Podemos reescrever o sinal da seguinte forma:

A constante do sinal pode ser interpretada como uma onda cossenoidal de frequência . Como o sinal é composto de duas ondas cossenoidais, há dois picos em no domínio da frequência, cada um ocorrendo na frequência de cada onda. Como uma das duas ondas tem frequência de , há um pico em . Legal, né?

Portanto, os picos no domínio da frequência ocorrem onde eram esperados.

Resposta

Gráfico do sinal no domínio do tempo:

Gráfico do sinal do domínio da frequência, tendo as frequências em no eixo X:

Os picos do sinal ocorrem onde eram esperados no domínio da frequência:

O primeiro ocorre em , correspondendo à frequência da primeira componente do sinal ();
O segundo ocorre em , correspondendo à frequência da segunda componente do sinal ().

Exercício Resolvido #5

“Adaptado de UnB - Laboratório 08: A Transformada Rápida de Fourier (FFT) e análise espectral”

Neste exercício, você encontrará o conteúdo de espectro e frequência do seu próprio sinal de voz.

Vá ao site https://online-voice-recorder.com/pt/ e grave uma fala sua. Você pode dizer o que quiser ou ler a frase abaixo:

“No Responde Aí, é como se você estivesse estudando do lado daquele amigo que sabe tudo.”

Escute ao sinal do seu áudio e então leia-o no MATLAB usando a função .
Determine o espectro de frequência do sinal de voz.
Plote o sinal no domínio do tempo e no domínio da frequência no mesmo gráfico, como na figura abaixo:

Passo 1

O exercício pede para gravarmos nossa própria voz e entrarmos com o arquivo de áudio no MATLAB (por meio de uma função que vamos conhecer no exercício de hoje, ) para vermos o sinal da nossa voz no domínio do tempo e no domínio da frequência.

Nossa voz, quando gravada, está no domínio do tempo. Para convertê-la para o domínio da frequência, usaremos a função .

Passo 2

Vamos começar pela letra a. Vamos no site recomendado pelo enunciado para gravarmos nossa voz. Ao abrir o site no navegador, você verá que tem um botão vermelho (indicado pela seta na figura abaixo), no qual você deve clicar para iniciar a gravação:

Ao iniciar a gravação, fale a frase que desejar ou a sugerida pelo enunciado. Para encerrar a gravação, aperte o botão de “Stop” no site (destacado abaixo).

Você pode escutar sua gravação antes de salvar o áudio em formato mp3, clicando no botão destacado abaixo.

Salve o áudio na pasta onde você salvará o script do MATLAB onde você escreverá o código deste exercício.

Passo 3

Feita a letra a, vamos fazer a letra b. Primeiro, escute o áudio que você gravou. Não se preocupe, eu te espero.

Em seguida, crie um script novo no MATLAB, salve-o na pasta onde você salvou a gravação da sua voz e digite o comando:

Esta é a função do MATLAB. Ela lê arquivos de áudio e tem como entrada um string do nome do arquivo de áudio a ser lido. No meu caso, eu salvei a gravação da minha voz como minha_voz.mp3, por isso a entrada do comando acima é . Lembre-se de alterar para o nome do seu arquivo de áudio.

A função retorna duas saídas: o vetor , que é o sinal do áudio do arquivo de entrada no domínio do tempo, e a frequência de amostragem do sinal.

Tendo concluído a letra b, vamos para a letra c.

Passo 4

Na letra , temos que determinar o espectro de frequência do sinal de voz, isto é, analisá-la no domínio da frequência. Para isto, usaremos a função do MATLAB no vetor , obtido no passo 3, que converte sinais no domínio do tempo para o domínio da frequência.

Digite em seu script o comando:

A função tem como entrada o vetor , que contém números reais representando o sinal da gravação da nossa voz no domínio do tempo. Já a saída é um vetor com números complexos: é a conversão de no domínio do tempo para o domínio da frequência. Os vetores e têm a mesma quantidade de elementos.

O vetor é o espectro de frequência do sinal de voz, logo, a letra c está concluída.

Passo 5

Vamos resolver a letra d, que pede pra plotarmos, em um mesmo gráfico, o sinal da nossa voz no domínio do tempo e no domínio da frequência.

Vamos começar gerando as informações para plotar o sinal no domínio do tempo. Precisamos criar um vetor que representará o domínio do tempo, em segundos, e será o eixo X do gráfico do sinal no domínio do tempo. O vetor será criado a partir do comando:

Neste comando, cria-se primeiro um vetor que vai de a , com passo de (). Este vetor tem elementos, correspondendo aos pontos medidos na nossa gravação de voz. Em seguida, esse vetor é multiplicado por , que é o período, em segundos, do sinal.

Precisamos, então, primeiro determinar e antes de calcular o vetor .

Como é o número de pontos medidos, ele corresponde ao número de elementos do vetor , que é o sinal de áudio no domínio do tempo. Logo, para obter, podemos fazer , pois a função retorna a quantidade de elementos de um vetor.

O período do sinal é o inverso da frequência de amostragem , isto é, . A frequência de amostragem foi obtida no passo 3, com o .

Logo, adicione em seu script os seguintes comandos para criar o vetor representando o domínio do tempo:

Por curiosidade: se você rodar o programa que digitou até agora e pedir ao MATLAB para ver o último elemento do vetor , com o comando , no Command Window, você verá que ele corresponde à duração da gravação do seu áudio, em segundos. No meu caso, minha gravação tinha um pouco mais de segundos:

Com os vetores e , conseguimos plotar o sinal da nossa voz no domínio do tempo.

Passo 6

Agora, vamos gerar as informações para plotar o espectro de frequência da gravação da nossa voz, isto é, o sinal de nossa voz no domínio da frequência.

Quando plotamos um sinal no domínio da frequência, normalmente temos no eixo vertical do gráfico a magnitude do sinal obtido pela função . Para calcular a magnitude, usamos a função do MATLAB. Digite no MATLAB a linha de código:

Com esta linha, calculamos a magnitude de cada elemento do vetor usando a função do MATLAB. Quando a entrada da função é um número complexo, ela calcula sua magnitude.

Agora precisamos criar o eixo horizontal do gráfico, representando o domínio da frequência. Para isto, digite os comandos:

Na segunda linha, geramos o domínio da frequência, representado pelo vetor . A lógica da sua criação é igualzinha à lógica que usamos para criar o vetor , do domínio do tempo.

Primeiramente, cria-se um vetor que vai de a , com passo de (). Este vetor tem elementos, correspondendo aos pontos capturados do sinal da nossa gravação. Em seguida, esse vetor é multiplicado por . Desta forma, é criado o domínio da frequência, que vai de a

Com os vetores e , conseguimos plotar o sinal da nossa voz no domínio da frequência.

Passo 7

Pra gerar o gráfico pedido na letra d, usaremos o comando do MATLAB.

Digite em seu script as seguintes linhas de código para gerar o gráfico:

Na primeira linha, com o comando , pedimos ao MATLAB para dividir a janela onde serão gerados os gráficos em uma “tabela” de duas linhas e uma coluna. Em seguida, indicamos que vamos plotar o gráfico da primeira linha da “tabela”.

Na segunda linha, com o comando o gráfico do sinal da nossa voz no domínio do tempo é gerado.

Na terceira linha, indicamos que o eixo horizontal do gráfico é o domínio do tempo por meio do comando .

Na quarta linha, indicamos que vamos plotar o segundo gráfico, na segunda linha da “tabela” criada pelo .

Em seguida, na quinta linha, o gráfico da magnitude de no domínio da frequência é criado com o comando Repare que, para plotar, usamos somente a primeira metade dos vetores com elementos e . Isso é indicado pela adição de à direita do nome do vetor, que diz ao MATLAB que queremos pegar do primeiro elemento ao elemento do vetor.

Usamos somente a primeira metade dos vetores e porque, no domínio da frequência, a partir de , as magnitudes começam a se repetir e não precisamos pôr elas no gráfico.

Finalmente, na última linha, indicamos que o eixo horizontal do gráfico é o domínio da frequência por meio do comando .

Ao executar o programa, teremos o gráfico pedido na letra d.

Resposta

A figura abaixo contém o gráfico do sinal da gravação de áudio no domínio do tempo (gráfico acima) e o gráfico do sinal no domínio da frequência (gráfico abaixo)

Exercício Resolvido #6

“Adaptado de UFRJ – MATLAB Exercises. Chapter 3 – Digital Filters, de Isabela F. Apolinário e Camila M. G. Gussen”

O sinal foi amostrado a uma taxa de amostras por segundo durante segundos.

Plote o sinal
Estime o espectro desse sinal usando . Plote a magnitude do sinal no domínio da frequência
Estime de novo o espectro do sinal. Desta vez, adicione zeros no final do sinal de forma que seu comprimento seja igual ao dobro do comprimento original. Plote sua magnitude no domínio da frequência
Considerando as letras [b.] e [c.], por que existem dois picos principais?
Considerando a letra [b.], quais são as frequências (em ) dos dois picos? Por que estes picos estão nessas frequências?
Considerando a letra [c.], quais são as frequências (em ) dos dois picos? Por que estes picos estão nessas frequências?
Por que a frequência onde ocorre o primeiro pico das letras [e.] e [f.] é diferente? Qual letra ([e.] ou [f.]) tem a estimativa mais precisa? Como este resultado poderia ser melhorado?

Passo 1

Neste exercício, vamos calcular a transformada de Fourier de considerando duas quantidades diferentes de pontos de medição. Desta forma, vamos poder ver o impacto do númeto de pontos medidos sobre a precisão dos resultados no espectro da frequência.

Quando a questão pede para “estimar o espectro” do sinal, na prática ele pede para aplicarmos em e plotar o gráfico da magnitude do sinal no domínio da frequência.

Passo 2

A letra a do exercício pede para plotarmos . Para fazermos isso, precisamos criar um vetor representando o intervalo de tempo da medição, que vai de a segundos. Para construir esse vetor, precisamos do período da amostra, que é definido como o inverso da frequência de amostragem, isto é, . O enunciado diz que , por isso, em um script novo do MATLAB, defina o período com as linhas de código:

Com calculado, podemos criar o vetor representando o intervalo de a . Para criar o vetor , usaremos o comando:

O enunciado não nos dá o número de pontos , mas podemos calculá-lo sabendo a medição durou . Isto quer dizer que o vetor deve começar em e terminar em . Logo, o último elemento de deve ser igual a:

Como conhecemos , podemos obter a partir da equação acima. Temos que é igual a:

No seu script, entre com essa equação para calcular , construa o vetor e entre com :

Com isso, temos tudo o que precisamos para plotar . Digite as linhas de código abaixo no seu script para plotar no domínio do tempo:

Na primeira linha, pedimos ao MATLAB para gerar uma figura com o comando , para termos o gráfico no domínio do tempo em uma janela diferente dos gráficos no domínio da frequência (que geraremos mais pra frente, pra resolver as letras b e c, no mesmo script).

Em seguida, com o comando o gráfico de , no domínio do tempo, é efetivamente gerado.

Indicamos que o eixo horizontal do gráfico é o domínio do tempo por meio do comando . Temos no eixo vertical do gráfico os valores de , indicados por .

Ao rodarmos o programa, temos a solução da letra a:

Passo 3

A letra b pede para estimar o espectro do sinal usando , em outras palavras, para calcular o sinal no domínio da frequência. Para isto, usaremos a função do MATLAB, que tem a seguinte estrutura:

A entrada da função é um vetor contendo dados no domínio do tempo, representados por números reais. Já a saída é um vetor com números complexos: é a conversão de no domínio do tempo para o domínio da frequência. Os vetores e têm a mesma quantidade de elementos.

Digite no seu script o comando:

Com esta linha de código, o MATLAB passará o sinal , que está no domínio do tempo e é representada pelo vetor , para o domínio da frequência. O sinal no domínio da frequência é representada pelo vetor .

A letra b também pede para plotar a magnitude do sinal no domínio da frequência. Vamos calcular a magnitude usando a função do MATLAB. Digite no MATLAB a linha de código:

Com esta linha, calculamos a magnitude de cada elemento do vetor .

Já temos o eixo vertical do gráfico, agora precisamos criar o eixo horizontal, representando o domínio da frequência. Para isto, digite os comandos:

Na segunda linha, geramos o domínio da frequência, representado pelo vetor . A lógica da sua criação é igualzinha à lógica que usamos para criar o vetor , do domínio do tempo.

Primeiramente, cria-se um vetor que vai de a , com passo de (), com elementos. Em seguida, esse vetor é multiplicado por . Desta forma, é criado o domínio da frequência, que vai de a

Após criar o domínio da frequência, vamos usar novamente a função para gerar o gráfico da magnitude do sinal no domínio da frequência:

Na primeira linha, pedimos ao MATLAB para gerar uma segunda figura com o comando , para termos o gráfico no domínio da frequência em uma janela diferente do gráfico no domínio do tempo.

Em seguida, o gráfico da magnitude de no domínio da frequência é criado com o comando Indicamos que o eixo horizontal do gráfico é o domínio da frequência por meio do comando . Temos no eixo vertical do gráfico a magnitude de , indicado por .

Execute o programa para ter a solução da letra b:

Passo 4

A letra c pede para calcular novamente o sinal no domínio da frequência, mas adicionando zeros no final do sinal para dobrar o comprimento original. Para adicionar os zeros no sinal, vamos concatenar o vetor , que representa o sinal , com um vetor de zeros que tenha o mesmo comprimento de , adicionando ao nosso script a linha de código:

Nesta linha, criamos um vetor de zeros com a função do MATLAB, que cria uma matriz de zeros com uma linha e colunas. O comando retorna o número de elementos do vetor . Portanto, vai nos dar um vetor de zeros de mesmo tamanho de .

A concatenação dos vetores é feita colocando-os dentro de colchetes. Isto cria um vetor cuja primeira metade dos elementos é igual a e a segunda metade, um monte de zeros.

Vamos calcular o sinal novo no domínio da frequência, usando :

O novo sinal no domínio da frequência é representada pelo vetor .

A letra c também pede para plotar a magnitude do sinal novo no domínio da frequência. Novamente, vamos usar a função para calcular a magnitude :

O resultado é armazenado no vetor , que será o eixo vertical do gráfico.

Precisamos recriar o eixo horizontal representando o domínio da frequência, pois a adição dos zeros alterou o número de pontos da medição. O novo número de pontos é igual à quantidade de elementos de , dada pela função :

Com o novo número de pontos, precisamos recalcular o passo do domínio da frequência e atualizar o domínio da frequência, com os comandos:

O novo passo é e o novo domínio é o vetor .

vamos usar novamente a função para plotar a magnitude do novo sinal no domínio da frequência:

Na primeira linha, pedimos ao MATLAB para gerar uma terceira figura com o comando . Em seguida, o gráfico da magnitude de no domínio da frequência é criado com o comando

Execute o programa para ter a solução da letra c:

Passo 5

A letra d pergunta por que os dois gráficos no domínio da frequência tem dois picos principais. Isso ocorre porque a função do MATLAB é válida para um intervalo no domínio da frequência que vai de . A partir de , os resultados da se repetem, de forma espelhada. Na prática, poderíamos só plotar a primeira metade do gráfico.

Passo 6

A letra e pergunta em quais frequências ocorrem os dois picos no gráfico gerado na letra b e por que os picos ocorrem nessas frequências.

No print abaixo temos o gráfico da letra com as coordenadas dos dois picos:

O primeiro pico ocorre a uma frequência de e o segundo, a (que é exatamente igual a , reforçando a resposta da letra d).

O gráfico acima é o sinal no domínio da frequência. A frequência de é igual a:

Os picos de sinais periódicos no domínio da frequência ocorrem na frequência máxima do sinal quando a frequência de amostragem () é pelo menos o dobro da frequência da onda (). Este é o teorema de amostragem de Nyquist. No gráfico acima, o primeiro pico ocorre a , uma frequência muito próxima de . Isso ocorre porque o teorema de amostragem de Nyquist foi respeitado.

Passo 7

A letra f pergunta em quais frequências ocorrem os dois picos no gráfico gerado na letra c e por que os picos ocorrem nessas frequências.

No print abaixo temos o gráfico da letra com as coordenadas dos dois picos:

O primeiro pico ocorre a uma frequência de e o segundo, a (que é exatamente igual a ).

O gráfico acima é o sinal com o dobro de pontos no domínio da frequência. Como vimos no passo anterior, a frequência de é igual a . Como neste caso o teorema de amostragem de Nyquist também foi respeitado, temos que o primeiro pico ocorre a uma frequência muito próxima de , até mais próxima do que o caso original.

Passo 8

A letra g pergunta por que a frequência onde ocorre o primeiro pico das letras e e g é diferente, qual das duas tem a estimativa mais precisa e como podemos melhorar o resultado.

A frequência onde ocorrem os picos é diferente porque o número de pontos da amostra é diferente (). A letra g, que tem o espectro de com o dobro de pontos, é a estimativa mais precisa, exatamente por ter mais pontos. Isso é evidenciado pelo fato de o primeiro pico da letra g ocorre em uma frequência () mais próxima à frequência de (). Para melhorar o resultado, podemos diminuir o período de amostragem, ou seja, podemos aumentar a frequência de amostragem . Isso faz com que tenhamos mais pontos na amostra, deixando o resultado mais preciso.

Resposta

A função do MATLAB é válida para um intervalo no domínio da frequência que vai de . A partir de , os resultados da se repetem, de forma espelhada.
O primeiro pico ocorre a uma frequência de e o segundo, a . Segundo o teorema de amostragem de Nyquist, os picos de sinais periódicos no domínio da frequência ocorrem na frequência máxima do sinal no domínio do tempo quando a frequência de amostragem é pelo menos o dobro da frequência da onda.
O primeiro pico ocorre a uma frequência de e o segundo, a . Os picos ocorrem nessa frequência por causa do teorema de amostragem de Nyquist.
A frequência onde ocorrem os picos é diferente porque o número de pontos da amostra é diferente. A letra g, que tem o espectro de com o dobro de pontos, é a estimativa mais precisa. Isso é evidenciado pelo fato de o primeiro pico da letra g ocorre em uma frequência () mais próxima à frequência de (). Para melhorar o resultado, podemos diminuir o período de amostragem, ou seja, podemos aumentar a frequência de amostragem . Isso faz com que tenhamos mais pontos de medição, deixando o resultado mais preciso.

Exercício Resolvido #7

“Adaptado de UFC – Apostila de MATLAB – PET Elétrica. Exercício 25, p. 86 (2014)”

Uma propriedade da Transformada de Fourier é que a transformada da convolução de duas funções equivale à multiplicação das duas no domínio da freqüência. Portanto, para calcular a convolução de uma função levamos os dois sinais para o domínio da freqüência, os multiplicamos e voltamos para o domínio do tempo.

Digamos que você queira calcular a convolução das funções e . Você pode fazer isso da seguinte maneira:

Considerando essa propriedade, calcule a convolução das formas de onda:

Passo 1

Neste exercício, vamos usar o comando e (comando novo que vamos aprender aqui!) para calcular . No nosso programa, vamos primeiramente entrar com e no domínio do tempo. Em seguida, aplicaremos em e a função do MATLAB para calcular as funções no domínio da frequência e então multiplicaremos os resultados entre si.

No resultado da multiplicação, vamos usar a função do MATLAB , que calcula a inversa da transformada de Fourier, para voltar ao domínio do tempo. A saída de é a convolução de e e a solução do exercício.

Passo 2

Em um script novo, vamos criar um vetor representando o domínio do tempo e, em seguida, entrar com e :

Na primeira linha, criamos o vetor , que vai de a , com um passo de .

Na segunda e na terceira linha, calculamos e para cada elemento do vetor . Os resultados são armazenados nos vetores e , respectivamente. Portanto, os vetores e representam e em um domínio de tempo .

Para ver a cara de e plotando suas curvas em um mesmo gráfico, digite os comandos abaixo:

Na primeira linha, pedimos ao MATLAB para gerar uma figura com o comando , para termos o gráfico de e em uma janela diferente do gráfico do resultado da convolução (que será gerado mais pra frente). Em seguida, com o comando as curvas de em função de e em função de são geradas.

O comando fará com que o gráfico tenha uma legenda, indicando quem é e quem é . As legendas dentro de devem estar na mesma ordem das curvas em .

Execute o programa para ver o gráfico de e :

Passo 3

Após definir e , vamos aplicar a transformada de Fourier neles para calculá-los no domínio da frequência. Para isto, usaremos a função do MATLAB, que tem a sintaxe:

Logo, digite em seu programa as duas linhas de código:

Na primeira linha, calculamos a transformada de Fourier de e armazenamos o resultado em . Na segunda linha, fazemos a mesma coisa pata , cuja transformada é armazenada em .

O próximo passo é multiplicar as funções no domínio da frequência uma pela outra. Para isto, multiplicaremos o vetor por , elemento a elemento, entrando com a seguinte linha de código:

Usando o operador , multiplicamos cada elemento de pelo elemento de que está na mesma posição. O resultado dessa operação é armazenado em , que representa a convolução no domínio da frequência.

Passo 4

O vetor está no domínio da frequência e teremos o resultado da convolução ao passá-lo para o domínio do tempo. Para isto, usaremos a função do MATLAB, que tem a sintaxe:

A entrada da função é um vetor contendo dados no domínio da frequência, representados por números complexos. Já a saída é um vetor com números reais: é a conversão de no domínio da frequência para o domínio do tempo. Os vetores e têm a mesma quantidade de elementos.

Resumindo, faz o inverso de , calculando a transformada de Fourier inversa de uma função no domínio da frequência.

Portanto, inclua em seu código o comando:

Para ver o resultado da convolução, plote em função de (o domínio do tempo) com as linhas de código:

Na primeira linha, pedimos ao MATLAB para gerar uma segunda figura com o comando , para termos o gráfico do resultado da convolução em uma janela separada do primeiro gráfico. Em seguida, usamos o comando para plotar a curva da solução da convolução . Execute o programa para ver o gráfico.

Resposta

Exercício Resolvido #8

“Adaptado de University of Texas at Dallas – Fast Fourier Transform and MATLAB Implementation, de Wanjun Huang para Dr. Duncan L. MacFarlane”

O sinal de uma onda quadrada com frequência de tem pontos e foi amostrado a uma taxa de amostras por segundo. Plote a onda quadrada no domínio do tempo e use o método da transformada de Fourier para plotar a magnitude do sinal no domínio da freqüência.

Passo 1

O exercício pede para plotarmos uma onda quadrada no domínio do tempo e sua magnitude no domínio da frequência. Para criar a onda quadrada no domínio do tempo, vamos aprender uma função nova do MATLAB: .

Tendo criado a onda com , aplicaremos a função na onda para termos a transformada de Fourier dela e plotar sua magnitude no domínio da frequência.

Passo 2

Primeiramente, vamos entrar no MATLAB as informações fornecidas pelo enunciado: a frequência da onda quadrada, a taxa de amostragem e o número de pontos :

Em seguida, podemos calcular o período de amostragem (que é o inverso de ) e criar um vetor representando o domínio do tempo:

Para construir o vetor , cria-se primeiro um vetor que vai de a , com passo de (). Este vetor tem elementos, correspondendo aos pontos do sinal. Em seguida, esse vetor é multiplicado por .

Tendo definido o domínio do tempo, podemos construir a onda quadrada, por meio do comando , que tem a sintaxe:

Ela retorna uma onda quadrada de amplitude com frequência para um vetor representando o tempo. A onda quadrada é armazenada no vetor .

Em seu programa, adicione o comando:

Este comando gerará a onda quadrada de frequência com vetor que criamos acima. Note que a frequência foi convertida de para , fazendo .

Passo 3

Para plotar a onda quadrada no domínio do tempo, entre com as linhas de código:

Na primeira linha, pedimos ao MATLAB para gerar uma figura com o comando , para termos o gráfico no domínio do tempo em uma janela diferente do gráfico no domínio da frequência. Em seguida, com o comando o gráfico da onda quadrada no domínio do tempo é efetivamente gerado.

Indicamos que o eixo horizontal do gráfico é o domínio do tempo por meio do comando . Temos no eixo vertical do gráfico os valores de , indicados por .

Rodando o programa, temos o gráfico da onda quadrada:

Passo 4

Vamos aplicar o método da transformada de Fourier para plotar a magnitude do sinal no domínio da frequência. Para isto, usaremos a função do MATLAB, que tem a seguinte estrutura:

Digite no seu script o comando:

Com esta linha de código, o MATLAB passará o sinal da onda quadrada no domínio do tempo, representada pelo vetor , para o domínio da frequência. O sinal no domínio da frequência é representada pelo vetor .

Passo 5

Após aplicar a transformada de Fourier, vamos calcular a magnitude do sinal no domínio da frequência. Para isto, usaremos a função do MATLAB. Digite no MATLAB a linha de código:

Com esta linha, calculamos a magnitude de cada elemento do vetor .

Já temos o eixo vertical do gráfico da onda quadrada no domínio da frequência, agora precisamos criar o eixo horizontal, representando o domínio da frequência. Para isto, digite os comandos:

Na segunda linha, geramos o domínio da frequência, representado pelo vetor . A lógica da sua criação é igualzinha à lógica que usamos para criar o vetor , do domínio do tempo.

Primeiramente, cria-se um vetor que vai de a , com passo de (), com elementos. Em seguida, esse vetor é multiplicado por . Desta forma, é criado o domínio da frequência, que vai de a

Passo 6

Após criar o domínio da frequência, vamos usar novamente a função para gerar o gráfico da magnitude do sinal no domínio da frequência:

Na primeira linha, pedimos ao MATLAB para gerar uma segunda figura com o comando , para termos o gráfico no domínio da frequência em uma janela diferente do gráfico no domínio do tempo.

Indicamos que o eixo horizontal do gráfico é o domínio da frequência por meio do comando . Temos no eixo vertical do gráfico a magnitude de , indicado por .

Execute o programa e você terá a magnitude da onda quadrada no domínio da frequência:

Resposta

Onda quadrada no domínio do tempo

Magnitude da onda quadrada no domínio da frequência

Transformada de Fourier

Teoria

Introdução

A função do MATLAB fft

Domínio do Tempo versus Domínio da Frequência

Exemplo no MATLAB

Domínio do Tempo versus Domínio da Frequência Ver mais

Exemplo no MATLAB Ver mais

Exercícios Resolvidos

Exercício Resolvido #1

Passo 1

Passo 2

Passo 3

Passo 4

Passo 5

Resposta

Exercício Resolvido #2

Passo 1

Passo 2

Passo 3

Passo 4

Passo 5

Resposta

Exercício Resolvido #3

Passo 1

Passo 2

Passo 3

Passo 4

Passo 5

Resposta

Exercício Resolvido #4

Passo 1

Passo 2

Passo 3

Passo 4

Passo 5

Resposta

Exercício Resolvido #5

Passo 1

Passo 2

Passo 3

Passo 4

Passo 5

Passo 6

Passo 7

Resposta

Exercício Resolvido #6

Passo 1

Passo 2

Passo 3

Passo 4

Passo 5

Passo 6

Passo 7

Passo 8

Resposta

Exercício Resolvido #7

Passo 1

Passo 2

Passo 3

Passo 4

Resposta

Exercício Resolvido #8

Passo 1

Passo 2

Passo 3

Passo 4

Passo 5

Passo 6

Resposta

Domínio do Tempo versus Domínio da Frequência

Exemplo no MATLAB