Teoria
Introdução
E aí, pessoal, tudo joia? Na aula de hoje, vamos aprender uma ferramenta muito útil para nós, engenheiros. Você já deve ter ouvido muito a palavra “otimizar”, né? No dia a dia, a gente tenta muito “otimizar nosso tempo”, tentando encontrar as condições favoráveis que permitam que a gente faça muitas tarefas num intervalo mínimo de tempo.
Mas sabia que também otimizamos muitas coisas em projetos de engenharia? Digamos que você vai projetar um canal de irrigação, com esta seção transversal:
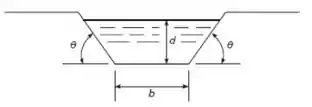
O canal tem profundidade , base e ângulo lateral . Você quer otimizar o uso do concreto para construir o canal, de forma a gastar o mínimo possível. Para isto, você precisa encontrar o menor perímetro possível da seção transversal, mantendo uma área de , necessária para transportar o fluxo de água desejado.
Como você faria isso? De certa forma, de maneira parecida com que você tenta “otimizar seu tempo”: você vai determinar as variáveis do seu dia para realizar suas tarefas no mínimo de tempo possível. No projeto do canal de irrigação, você vai determinar as dimensões e e o ângulo que deem o menor perímetro possível.
Nas ciências exatas, esse processo de encontrar as variáveis que nos deem o menor valor possível de alguma coisa é chamado de “otimização”. Usamos muito otimização para dimensionar máquinas e equipamentos, reduzirmos custos de produção, desenvolver redes neurais, entre outras aplicações.
Conhecer ferramentas de otimização ajuda muuuuuito em projetos de engenharia. Se a gente não tivesse otimização, provavelmente teríamos que testar várias alternativas até encontrar um resultado que atendesse à nossa necessidade, o que toma muito tempo e é muito cansativo. Conhecendo otimização, podemos atacar o problema de forma muito mais efetiva em um projeto ;D

Existem várias técnicas de otimização e o MATLAB tem muuuuuitas funções para otimizarmos alguma coisa. Na aula de hoje, vamos conhecer uma delas, a função .
Mas antes, temos que aprender a identificar um problema onde podemos aplicar otimização.
Identificando um problema de otimização
Em engenharia, chamamos de “problema de otimização” um problema onde queremos encontrar a melhor solução dentre as soluções possíveis. A melhor solução pode ser o mínimo ou o máximo valor de alguma de coisa.
Essa “alguma coisa” é uma função representando o que queremos minimizar ou maximizar e é chamada de função objetivo. No exemplo do canal de irrigação, queremos minimizar o perímetro, logo, o perímetro do canal é a função objetivo.
A função objetivo depende de algumas variáveis, chamadas de variáveis de projeto. Na otimização, queremos encontrar os valores das variáveis de projeto que minimizem/maximizem a função objetivo. Para o exemplo do canal de irrigação, as variáveis de projeto são as dimensões e e o ângulo .
Portanto, se eu quiser usar otimização para resolver algum problema, a primeira coisa que tenho que pensar é:
“O que eu quero minimizar/maximizar?”, para determinar a função objetivo.
“O que eu quero otimizar depende de quê?”, para ver quais as variáveis de projeto.

Tendo isso bem claro, podemos usar o MATLAB para resolver nosso problema. As entadas das funções do MATLAB que resolvem problemas de otimização normalmente são a função objetivo e as variáveis de projeto.
A função fminsearch
A função do MATLAB tem a forma:
Precisamos fornecer a ela no mínimo duas entradas:
- uma função representando a função objetivo;
- um vetor contendo um “chute” inicial das variáveis de projeto.
A saída de é um vetor contendo os valores das variáveis de projeto que minimizam a função objetivo.
Vamos usar o exemplo do canal de irrigação para vermos como a funciona, mas primeiro, vamos montar o “problema de otimização”.
Problema de otimização: canal de irrigação
Primeiramente, vamos identificar a função objetivo. Queremos minimizar o perímetro da seção transversal do canal de irrigação da figura abaixo:

O perímetro da seção transversal é dado por:
Onde é a profundidade do canal, é a base e é o ângulo lateral.
“Então esta é a minha função objetivo, certo? Já que eu quero encontrar o menor perímetro possível”, você deve estar pensando corretamente. “E as minhas variáveis de projeto são , e , já que depende delas”, o que também está correto.
Mas lembra que a gente quer manter a área da seção transversal em ? A área da seção transversal trapezoidal é:
Podemos usar a equação da seção transversal para reduzir o número de variáveis de projeto. Isolando na equação da seção transversal:
Podemos usar essa expressão no lugar de na equação de perímetro, gerando a seguinte equação:
Logo, nossa função objetivo é:
E nossas variáveis de projeto são e .
Com o problema de otimização bem estruturadinho, podemos partir para o MATLAB.
Usando fminsearch para projetar o canal
Vamos começar entrando com a função objetivo do problema de otimização. Para isto, vamos criar uma função no MATLAB, em um script novo:

Com as linhas de código acima, criamos uma função chamada , que contém a equação que calcula o perímetro do canal. A função tem como entrada um vetor com dois elementos, representando as variáveis de projeto. O primeiro elemento de , , corresponde à profundidade do canal e o segundo elemento, , ao ângulo . A saída da função é o perímetro do canal de irrigação.
Note que as funções trigonométricas e têm como entrada um ângulo em radianos.
Os comentários indicando as variáveis de projeto são opcionais, mas é sempre bom colocar pra você não se perder nos programas :)
Após criar a função , vamos usar para encontrar os valores de e que deem o menor perímetro possível. Em um novo script, vamos digitar as linhas de código:
![]()
Na primeira linha, entramos com nosso “chute” inicial das variáveis de projeto: e .
Na segunda linha, usamos . Para indicar a função objetivo em , usamos o nome da função criada com a função objetivo com um na frente. Por isso a primeira entrada de , neste caso, é .
A saída de é o vetor com os valores de e que dão o menor perímetro possível.
Bora rodar o programa? Ao executar nosso código, temos que o vetor é igual a:

Isto quer dizer que, para o nosso “chute” inicial, os valores de e que minimizam o perímetro do canal são e .
Para sabermos o valor do perímetro com esses valores de e , incluímos a seguinte linha de código logo abaixo de :
![]()
Com este comando, usamos a função que criamos para calcular , tendo como entrada o vetor dado por .
Para e , temos que o perímetro equivale a:

Vale destacar que a saída de depende do nosso “chute” inicial. Se usarmos um diferente de , podemos chegar a uma solução diferente. Isso porque nos dá um mínimo local de uma função. Um mínimo local é um ponto em uma função cujo valor é o menor entre os pontos próximos, mas pode ser maior do que um ponto mais distante.
Para entendermos o que é um mínimo local, observe o gráfico abaixo, que representa o polinômio:
No intervalo .

Perceba que ele tem dois pontos que podem ser considerados “mínimos”, destacados em vermelho, dependendo do intervalo de procura. Por exemplo, se usarmos como valor inicial em , aplicada nesse polinômio, o MATLAB vai nos dizer que o valor de que minimiza é , dando .
Entretanto, se usarmos , o vai nos dizer que nos dá o menor possível: . Considerando os pontos mais próximos de , o ponto de coordenadas é um mínimo local. Mas perceba que ele é maior do que o ponto de coordenadas .
Por isso, a escolha do “chute” inicial é importante. Nos problemas de otimização, vale à pena gerar gráficos e usar diferentes “chutes” iniciais para tentar encontrar a melhor solução possível.
Para encerrar, nessa aula, resolvemos um problema de otimização que procurava o valor mínimo de uma função. Se quisermos encontrar o valor máximo de uma função, o passo a passo é o mesmo, o que muda é que devemos pôr um sinal de menos na frente da função objetivo.
Para o exemplo do canal, no MATLAB ficaria assim:

Ufa! Essa aula foi pesada, né? Agora bora praticar bastante com os exercícios para fixar o conteúdo de otimização ;D
Identificando um problema de otimização
A função fminsearch
Problema de otimização: canal de irrigação
Usando fminsearch para projetar o canal
Exercícios Resolvidos
Exercício Resolvido #1
“UFRJ – Computação Científica – Lista 3”
Como achar o mínimo da função com ?
Passo 1
O enunciado nos dá uma função e pede para encontrarmos o mínimo dela usando a função de otimização do MATLAB .
A primeira coisa que devemos entender bem antes de atacar o exercício é qual é o problema de otimização. Para isto, devemos ter muito claro:
- “O que eu quero minimizar?”, definindo a função objetivo;
- “O que eu quero minimizar depende do quê?”, definindo as variáveis de projeto.
O que queremos minimizar é a função dada no enunciado: queremos encontrar o valor mínimo de . Logo, a função é a função objetivo do problema de otimização.
A função do enunciado depende de . Logo, a variável de projeto é .
Em outras palavras, queremos encontrar o valor de que dê o menor possível.
Passo 2
Antes de partir para o MATLAB, vamos relembrar como é a função :
Precisamos fornecer a ela no mínimo duas entradas:
- uma função representando a função objetivo;
- um vetor contendo um “chute” inicial das variáveis de projeto.
A saída de é um vetor contendo os valores das variáveis de projeto que minimizam a função objetivo.
A primeira coisa que vamos fazer é entrar no MATLAB a função dada no enunciado. Em um script novo, crie uma função contendo a equação :

Chamei a função que contém a função objetivo de , mas você pode chamar do que quiser. tem como entrada a variável , que é a variável de projeto do problema de otimização. A saída de é a variável , que é o que queremos minimizar.
Após criar um script com a função objetivo, vamos implementar a . Em um novo script, salvo na mesma pasta onde está o script da função , digite as linhas de código:
![]()
Na primeira linha, entramos com o “chute” inicial da variável , armazenado na variável . Escolhi , mas você pode adotar outro valor.
Na segunda linha, usamos . Para indicar a função objetivo em , usamos o nome da função criada com a função objetivo com um na frente. Por isso a primeira entrada de , neste caso, é (caso tenha dado um nome diferente, não esqueça de trocar!). O algoritmo de otimização por trás de vai procurar o mínimo da função objetivo, isto é, o menor valor possível de , partindo de .
A saída de é a variável com o valor de que dá o menor possível.
Vamos rodar o programa para ver o que o vai retornar:
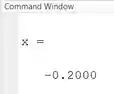
O valor de que dá o menor possível na função é .
Passo 3
Para ver qual é o valor mínimo de , acrescente no código o comando:
![]()
Com este comando, calculamos usando a função , tendo como entrada a saída de .
Rodando o programa, temos:

Logo, o menor valor possível de na função é , obtido quando .
Passo 4
Uma coisa legal de ver é se o mínimo encontrado pelo é o mesmo mínimo que encontramos quando procuramos o ponto de mínimo no gráfico da função.
Para entendermos o motivo, vamos plotar o gráfico de
Em um novo script, para plotar , digite as linhas de código:
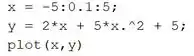
Na primeira linha, criamos um vetor que vai de a , com um passo de . Esse vetor vai ser o eixo horizontal do gráfico.
Na segunda linha, calculamos para cada elemento do vetor e armazenamos os resultados no vetor . O vetor será o eixo vertical do gráfico.
Na terceira linha, o gráfico de é gerado.
Executando o programa, temos o gráfico de :

Podemos encontrar no gráfico as coordenadas do ponto mínimo da função, clicando nele (como na figura acima). Veja que são exatamente e , dando o mesmo resultado de .
Resposta
As coordenadas do mínimo da função é e .
Exercício Resolvido #2
“UFRJ – Computação Científica – Lista 3”
Como achar o máximo da função com ?
Passo 1
O enunciado nos dá uma função e pede para encontrarmos o máximo dela usando a função de otimização do MATLAB .
A primeira coisa que devemos entender bem antes de atacar o exercício é qual é o problema de otimização. Para isto, devemos ter muito claro:
- “O que eu quero maximizar?”, definindo a função objetivo;
- “O que eu quero maximizar depende do quê?”, definindo as variáveis de projeto.
O que queremos maximizar é a função dada no enunciado: queremos encontrar o valor máximo de . Logo, a função é a função objetivo do problema de otimização.
A função do enunciado depende de . Logo, a variável de projeto é .
Passo 2
Antes de partir para o MATLAB, vamos relembrar como é a função :
Precisamos fornecer a ela no mínimo duas entradas:
- uma função representando a função objetivo;
- um vetor contendo um “chute” inicial das variáveis de projeto.
A saída de é um vetor contendo os valores das variáveis de projeto que minimizam a função objetivo.
“Ué, mas não queremos encontrar o máximo da função?”, você deve estar se perguntando. Para encontrar o máximo de uma função, podemos também usar , mas devemos colocar um sinal de menos na frente da função objetivo, como veremos a seguir.
A primeira coisa que vamos fazer é entrar no MATLAB a função dada no enunciado. Em um script novo, crie uma função contendo a equação :

Chamei a função que contém a função objetivo de , mas você pode chamar do que quiser. tem como entrada a variável , que é a variável de projeto do problema de otimização. A saída de é a variável , que é o que queremos maximizar.
Como queremos encontrar o máximo da função, vamos colocar um sinal de menos na frente da função objetivo, com se estivéssemos multiplicando ela por :

Logo, a função objetivo torna-se .
Em outras palavras, maximizar é a mesma coisa que minizar .
Após criar um script com a função objetivo, vamos implementar a . Em um novo script, salvo na mesma pasta onde está o script da função , digite as linhas de código:
![]()
Na primeira linha, entramos com o “chute” inicial da variável , armazenado na variável . Escolhi , mas você pode adotar outro valor.
Na segunda linha, usamos . Para indicar a função objetivo em , usamos o nome da função criada com a função objetivo com um na frente. Por isso a primeira entrada de , neste caso, é (caso tenha dado um nome diferente, não esqueça de trocar!). O algoritmo de otimização por trás de vai procurar o mínimo da função objetivo (que neste caso é ), isto é, o menor valor possível de , partindo de .
A saída de é a variável com o valor de que dá o menor possível.
Vamos rodar o programa e ver o que o MATLAB nos retorna:

Vixe, o MATLAB foi testando vários valores de , partindo de , e não conseguiu encontrar o mínimo de , isto é, o máximo de . Internamente na função , existe um limite de vezes que o MATLAB testa valores de . Se ele atinge esse limite e não encontra nenhum resultado, ele retorna a mensagem acima.
Passo 3
Mas por que será que o MATLAB não conseguiu encontrar o máximo de ? Para entendermos o motivo, vamos plotar o gráfico de
Em um novo script, digite as linhas de código:

Na primeira linha, criamos um vetor que vai de a , com um passo de . Esse vetor vai ser o eixo horizontal do gráfico.
Na segunda linha, calculamos para cada elemento do vetor e armazenamos os resultados no vetor . O vetor será o eixo vertical do gráfico.
Na terceira linha, o gráfico de é gerado.
Executando o programa, temos o gráfico de :
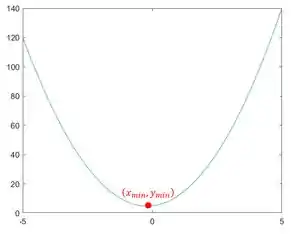
Note bem que a função representa uma parábola com concavidade para cima, logo, ela possui um ponto mínimo com coordenadas , destacado em vermelho na figura, mas não possui um ponto de máximo.
Quanto mais eu me afasto de , mais o aumenta, não havendo um “teto”. Por isso o MATLAB não conseguiu encontrar um ponto de máximo da função .
Resposta
Não é possível encontrar o máximo de pois se trata de uma parábola com concavidade para cima.
Exercício Resolvido #3
“Adaptado de MATLAB for Engineering Applications, de William J. Palm III. Exercício T3.2-4, p. 134”
A função
Tem dois mínimos no intervalo . Encontre os valores de e de cada mínimo.
Passo 1
O enunciado nos dá uma função e diz que ela tem dois mínimos em um dado intervalo. Neste exercício, a função objetivo é e a variável de projeto é .
Para encontrarmos as coordenadas de cada mínimo da função, usaremos a função de otimização do MATLAB , variando o “chute inicial” do algoritmo.
Para termos uma noção de cada chute inicial, temos que plotar primeiro.
Passo 2
Em um novo script, digite as linhas de código abaixo par plotar :

Na primeira linha, criamos um vetor que vai de a , com um passo de . Esse vetor representa o intervalo dado pelo enunciado e vai ser o eixo horizontal do gráfico.
Na segunda linha, calculamos para cada elemento do vetor e armazenamos os resultados no vetor . O vetor será o eixo vertical do gráfico.
Na terceira linha, o gráfico de é gerado. Executae o programa para vê-lo:
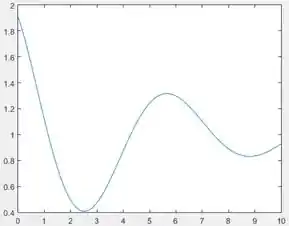
Passo 3
No gráfico de , podemos identificar os dois pontos de mínimo que o enunciado falou. Podemos achar mais ou menos suas coordenadas clicando na curva do gráfico:

Achar mínimos por gráficos é bom para se ter uma estimativa, mas se quisermos um resultado mais preciso, devemos usar algum algoritmo de otimização, que normalmente exigem um ponto de partida (ou “chute inicial”) para minimizar uma função.
Podemos escolher nossos “chutes iniciais” a partir do gráfico, por proximidade dos pontos que marcamos.
Passo 4
A função tem a sintaxe:
Precisamos fornecer a ela no mínimo duas entradas:
- uma função representando a função objetivo;
- um número representando um “chute” inicial da variável de projeto.
A saída de é uma variável contendo o valor da variável de projeto que minimiza a função objetivo.
Primeiramente, vamos definir a função objetivo que usaremos em usando o comando:
![]()
A função objetivo será armazenada em . O indica que é em função de , a nossa variável de projeto (não confundir com o vetor que criamos no passo 2).
Para encontrar o primeiro ponto de mínimo, o mais à esquerda, vamos adotar um “chute inicial” de :

O resultado de para é armazenado em , que é a coordenada do primeiro mínimo. A coordenada do primeiro mínimo é calculada entrando em e é armazenada em .
Temos que as coordenadas do primeiro ponto de mínimo são:

Para encontrar o segundo ponto de mínimo, vamos fazer o mesmo procedimento. Adote um “chute inicial” de :
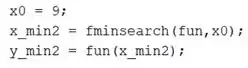
O resultado de para é armazenado em , que é a coordenada do segundo mínimo. A coordenada do segundo mínimo é calculada entrando em e é armazenada em .
Temos que as coordenadas do segundo ponto de mínimo são:

Resposta
As coordenadas do primeiro ponto de mínimo são e
As coordenadas do segundo ponto de mínimo são e
Exercício Resolvido #4
“Adaptado de An Engineer’s Guide to MATLAB® - With Applications from Mechanical, Aerospace, Electrical, Civil, and Biological Systems Engineering, de Edward B. Magrab et al, 3ª edição, 2011. Exercício 13.3, pp. 754-755”
A figura abaixo mostra um sistema de duas molas com uma carga (representado pelo desenho em linha cheia) e sem carga (desenho em linha tracejada):
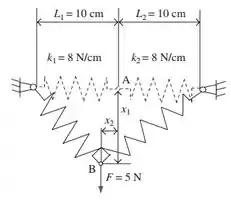
Após a carga ser aplicada no ponto , o sistema se deforma até atingir o equilíbrio no ponto , quando a energia potencial é mínima. A função da energia potencial () é dada pela equação abaixo:
Encontre a localização do ponto onde a energia potencial é mínima de duas maneiras:
- Plote a superfície e as curvas de nível da função ;
- Use com um ponto inicial .
Passo 1
O enunciado nos dá uma função e pede para que encontremos o mínimo dela usando dois métodos.
A primeira coisa que devemos entender bem antes de atacar o exercício é qual é o problema de otimização. Para isto, devemos ter bem claro:
- “O que eu quero minimizar?”, definindo a função objetivo;
- “O que eu quero minimizar depende do quê?”, definindo as variáveis de projeto.
O que queremos minimizar é a energia potencial do sistema de duas molas, representada pela função dada no enunciado:
Logo, a energia potencial do sistema de duas molas é minha função objetivo.
A função objetivo depende das variáveis e e de algumas constantes, todas indicadas na figura:
As variáveis e são as variáveis de projeto. Em outras palavras, queremos encontrar quanto e devem ser para que a energia potencial seja a menor possível.
Usaremos dois métodos para encontrar as coordenadas e que minimizam :
- Gerando a superfície e a curvas de nível: usaremos as funções e para gerar os gráficos. Se você não as conhece, não se preocupe, vamos ver tintim por tintim como elas funcionam;
- Usando , com um chute inicial .
Passo 2
Vamos começar pela letra a. Em um novo script, entre as constantes listadas no passo 1:

Em seguida, vamos criar dois vetores, e , representando uma faixa de valores que e podem assumir:
![]()
Os vetores e vão de a , com um passo de . Eles servirão para criar os eixos X e Y dos gráficos da superfície e das curvas de nível pedidos na letra a.
Para podermos usar as funções e do MATLAB, devemos criar matrizes a partir dos vetores e , que contêm as coordenadas dos vetores. Faremos isso usando a função :
![]()
A função pega os vetores e , que têm elementos, e cria duas matrizes quadradas e , de tamanho . Cada linha da matriz é o vetor , repetido vezes. Já cada coluna da matriz é o vetor , repetido vezes.
Para ver bem direitinho como o funciona, você pode rodar o script que você escreveu até agora e pedir ao MATLAB para imprimir e e compará-los, e fazer a mesma coisa para e .
A função serve para auxiliar na criação de gráficos em três dimensões. A matriz será o eixo X do gráfico da superfície e das curvas de nível da função . Já a matriz será o eixo Y.
O eixo Z dos gráficos será a energia potencial. Por isso temos que criar uma matriz de tamanho com os resultados de para cada elemento das matrizes e . Digite no MATLAB a função da energia potencial, substituindo e pelas matrizes e :
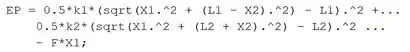
No print acima, eu “quebrei” a função em três linhas, para ela não ficar toda numa linha só e ficar ruim de ler. No MATLAB, fazemos quebras de linha colocando três pontos () onde queremos quebrar.
Repare também no uso do ponto ao lado das matrizes (por exemplo, ), ele indica que queremos realizar a operação em cada elemento da matriz.
Passo 3
Após ter criado as matrizes , e , podemos gerar os gráficos pedidos na letra a. Vamos começar com a superfície da função , que será gerada usando a função do MATLAB. A função tem o seguinte formato:
A plota uma superfície tridimensional com as curvas de nível abaixo dela. Ela gera um gráfico 3D com os valores da matriz no eixo X, da matriz no eixo Y e da matriz no eixo Z.
Vai dar para entender melhor aplicando a no exercício. Para gerar a superfície da função , adicione no script as seguintes linhas de código:

Na primeira linha, pedimos ao MATLAB para gerar uma figura com o comando , para termos o gráfico da superfície em uma janela diferente do gráfico das curvas de nível.
Na segunda linha, o comando cria a superfície da energia potencial, tendo no eixo X, no eixo Y e no eixo Z.
Na terceira linha, o comando faz com que o gráfico tenha uma barra de cores indicando a intensidade da energia potencial.
Na quarta linha, dizemos que o eixo X do gráfico corresponde à variável de projeto , com o comando .
Na quinta linha, dizemos que o eixo Y do gráfico corresponde à variável de projeto , com o comando .
Finalmente, na sexta linha, indicamos que o eixo Z do gráfico corresponde à energia potencial, com o comando .
Vamos executar o programa pra ver essa superfície:
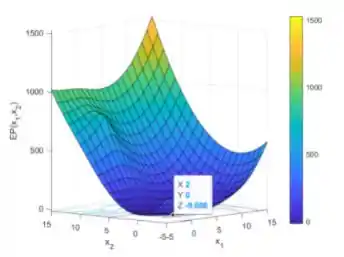
Repare que logo abaixo da superfície, no plano , temos as curvas de nível da superfície.
Para analisar a superfície e identificar o ponto de mínimo, na janela do gráfico, use o botão “Rotate 3D”, destacado abaixo, para “girar” a superfície.
Podemos ver as coordenadas dos pontos da superfície clicando neles. O ponto com menor que encontrei está marcado na superfície e tem coordenadas , e . Contudo, eu não tenho certeza se esse realmente é o ponto de mínimo.
É difícil encontrar o ponto exato de mínimo olhando só a superfície. Por isso, vamos gerar as curvas de nível em um gráfico separado para ver se facilita.
Passo 4
Para gerar um gráfico de curvas de nível, usaremos a função , que tem a seguinte estrutura:
Esse comando cria um gráfico de curvas de nível, onde as isolinhas (linhas que ligam pontos de mesmo valor) correspondem aos valores da matriz . As matrizes e definem o eixo X e o eixo Y do gráfico de curvas de nível.
Para criar o gráfico de curvas de nível, digite no seu script os comandos:

Na primeira linha, pedimos ao MATLAB para criar uma segunda figura com o comando , para que o gráfico de curvas de nível seja gerado em uma janela diferente da janela onde foi plotada a superfície, no passo 3.
Na segunda linha, o comando cria o gráfico das curvas de nível da energia potencial, tendo no eixo X, no eixo Y e dando os valores para as isolinhas. As strings no final do comando () pedem ao MATLAB para mostrar o valor de cada curva do gráfico.
Na terceira linha, indicamos que o eixo X do gráfico do gráfico corresponde à variável de projeto , com o comando .
Na quarta linha, dizemos que o eixo Y do gráfico corresponde à variável de projeto , com o comando .
Bora rodar o programa pra ver as curvas de nível:
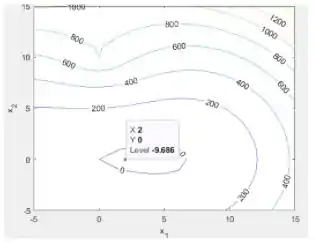
Repare que as curvas com menor estão mais no interior do gráfico e quanto mais afastados do centro, maior a intensidade de .
A curva de menor intensidade mostrada no gráfico é Isto significa que as coordenadas e que dão o mínimo estão no interior dessa curva e que a energia potencial mínima é pelo menos , mas pode assumir valores negativos. Podemos ver as coordenadas de certos pontos ao clicar sobre o ponto no gráfico. Na figura acima, achei o mesmo ponto de mínimo que encontrei no gráfico de superfície: as coordenadas , dão um .
Passo 5
Apesar de eu ter encontrado o mesmo ponto de mínimo, pode ser que na minha busca eu tenha deixado passar algum ponto com energia potencial menor. Por isso, vamos usar o para encontrar o ponto de mínimo de maneira mais precisa (e responder à letra b do exercício).
Antes de implementar o , vamos relembrar como ele é:
Precisamos fornecer a ela no mínimo duas entradas:
- uma função representando a função objetivo;
- um vetor contendo um “chute” inicial das variáveis de projeto.
A saída de é um vetor contendo os valores das variáveis de projeto que minimizam a função objetivo.
Vamos criar uma nova função no MATLAB para representar a função objetivo . Abra um script novo e digite:

Chamei a função que contém a função objetivo de , mas você pode chamar do que quiser. tem como entrada a variável , que é um vetor de dois elementos contendo as variáveis de projeto do problema de otimização: e . A saída de é a variável , que é a energia potencial que queremos minimizar.
Repare que tive que entrar novamente com as constantes da função , listadas no passo 1.
Após criar um script com a função objetivo, vamos implementar a . Em um novo script, salvo na mesma pasta onde está o script da função , digite as linhas de código:

Na primeira linha, entramos com o “chute” inicial das variáveis de projeto e , armazenado no vetor . O enunciado pediu para adotarmos .
Na segunda linha, usamos . Para indicar a função objetivo em , usamos o nome da função criada com a função objetivo com um na frente. Por isso a primeira entrada de , neste caso, é (caso tenha dado um nome diferente, não esqueça de trocar!). O algoritmo de otimização por trás de vai procurar o mínimo da função objetivo, isto é, o menor valor possível de , partindo de .
A saída de é o vetor , de dois elementos, com os valores de que dão o menor possível.
A terceira linha calcula o valor de usando a função , tendo como entrada o vetor dado por . Desta forma, encontramos a energia potencial mínima.
Vamos rodar o programa para ver o que o vai retornar e qual é a energia potencial mínima:
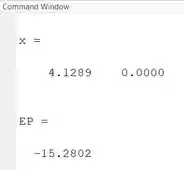
Encontramos que a energia potencial mínima é e ela ocorre em e .
Nossa, bem diferente dos valores que encontramos no gráficos, né? Pelo menos temos certeza que o resultado obtido usando é realmente o mínimo da função.
Resposta
A energia potencial mínima é e ela ocorre em e .
Exercício Resolvido #5
“Adaptado de An Engineer’s Guide to MATLAB® - With Applications from Mechanical, Aerospace, Electrical, Civil, and Biological Systems Engineering, de Edward B. Magrab et al, 3ª edição, 2011. Exercício 13.5, pp. 756-757”
A figura abaixo mostra dois carros A e B conectados por três molas lineares com rigidez igual a , e . Não há atrito no sistema.
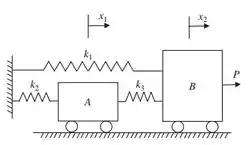
As molas estão em sua posição sem deformação quando a força aplicada é zero. A partir do seguinte problema de otimização para a função da energia potencial :
- Plote a superfície e as curvas de nível da função;
- Obtenha os deslocamentos otimizados e usando com ponto inicial e .
Passo 1
O enunciado nos dá uma função e pede para que encontremos o mínimo dela usando dois métodos.
A primeira coisa que devemos entender bem antes de atacar o exercício é qual é o problema de otimização. Para isto, devemos ter bem claro:
- “O que eu quero minimizar?”, definindo a função objetivo;
- “O que eu quero minimizar depende do quê?”, definindo as variáveis de projeto.
O que queremos minimizar é a energia potencial do sistema composto por dois carros conectados por molas, representada pela função dada no enunciado:
Logo, a energia potencial do sistema é minha função objetivo.
A função objetivo depende das variáveis e e de algumas constantes, como a rigidez das molas e a força , dadas pelo enunciado:
As variáveis e são as variáveis de projeto. Em outras palavras, queremos encontrar quanto e devem ser para que a energia potencial seja a menor possível.
Usaremos dois métodos para encontrar a posição dos carros A e B, representada por e , respectivamente, que minimizam :
- Gerando a superfície e a curvas de nível: usaremos as funções e para gerar os gráficos. Essas funções foram utilizadas no exercício anterior, mas vamos revê-las detalhadamente, para fixar bem como elas funcionam;
- Usando , com um chute inicial .
Passo 2
Vamos começar pela letra a. Em um novo script, entre as constantes listadas no passo 1:

Em seguida, vamos criar dois vetores, e , representando uma faixa de valores que e podem assumir:
![]()
Os vetores e vão de a , com um passo de . Eles servirão para criar os eixos X e Y dos gráficos da superfície e das curvas de nível pedidos na letra a.
Para podermos usar as funções e do MATLAB, devemos criar matrizes a partir dos vetores e , que contêm as coordenadas dos vetores. Faremos isso usando a função :
![]()
A função pega os vetores e , que têm elementos, e cria duas matrizes quadradas e , de tamanho . Cada linha da matriz é o vetor , repetido vezes. Já cada coluna da matriz é o vetor , repetido vezes.
Para ver bem direitinho como o funciona, você pode rodar o script que você escreveu até agora e pedir ao MATLAB para imprimir e e compará-los, e fazer a mesma coisa para e .
A função serve para auxiliar na criação de gráficos em três dimensões. A matriz será o eixo X do gráfico da superfície e das curvas de nível da função . Já a matriz será o eixo Y.
O eixo Z dos gráficos será a energia potencial. Por isso temos que criar uma matriz de tamanho com os resultados de para cada elemento das matrizes e . Digite no MATLAB a equação da energia potencial dada pelo enunciado, substituindo e pelas matrizes e :
![]()
Repare que usei o ponto ao lado das matrizes (por exemplo, ), para indicar que queremos realizar a operação em cada elemento da matriz.
Passo 3
Após ter criado as matrizes , e , podemos gerar os gráficos pedidos na letra a. Vamos começar com a superfície da função , que será gerada usando a função do MATLAB. A função tem o seguinte formato:
A plota uma superfície tridimensional com as curvas de nível abaixo dela. Ela gera um gráfico 3D com os valores da matriz no eixo X, da matriz no eixo Y e da matriz no eixo Z.
Vai dar para entender melhor aplicando a no exercício. Para gerar a superfície da função , adicione no script as seguintes linhas de código:

Na primeira linha, pedimos ao MATLAB para gerar uma figura com o comando , para termos o gráfico da superfície em uma janela diferente do gráfico das curvas de nível.
Na segunda linha, o comando cria a superfície da energia potencial, tendo no eixo X, no eixo Y e no eixo Z.
Na terceira linha, o comando faz com que o gráfico tenha uma barra de cores indicando a intensidade da energia potencial.
Na quarta linha, dizemos que o eixo X do gráfico corresponde à variável de projeto , com o comando .
Na quinta linha, dizemos que o eixo Y do gráfico corresponde à variável de projeto , com o comando .
Finalmente, na sexta linha, indicamos que o eixo Z do gráfico corresponde à energia potencial, com o comando .
Vamos executar o programa pra ver essa superfície:

Repare que logo abaixo da superfície, no plano , temos as curvas de nível da superfície.
Para analisar a superfície e identificar o ponto de mínimo, na janela do gráfico, use o botão “Rotate 3D”, destacado abaixo, para “girar” a superfície.

Podemos ver as coordenadas dos pontos da superfície clicando neles. O ponto com menor que encontrei tem coordenadas , e . Contudo, eu não tenho certeza se esse realmente é o ponto de mínimo, pois é difícil encontrar o ponto exato de mínimo olhando só a superfície.
Vamos gerar as curvas de nível em um gráfico separado para ver se facilita.
Passo 4
Para gerar um gráfico de curvas de nível, usaremos a função , que tem a seguinte estrutura:
Esse comando cria um gráfico de curvas de nível, onde as isolinhas (linhas que ligam pontos de mesmo valor) correspondem aos valores da matriz . As matrizes e definem o eixo X e o eixo Y do gráfico de curvas de nível.
Para criar o gráfico de curvas de nível, digite no seu script os comandos:

Na primeira linha, pedimos ao MATLAB para criar uma segunda figura com o comando , para que o gráfico de curvas de nível seja gerado em uma janela diferente da janela onde foi plotada a superfície, no passo 3.
Na segunda linha, o comando cria o gráfico das curvas de nível da energia potencial, tendo no eixo X, no eixo Y e dando os valores para as isolinhas. As strings no final do comando () pedem ao MATLAB para mostrar o valor de cada curva do gráfico.
Na terceira linha, indicamos que o eixo X do gráfico do gráfico corresponde à variável de projeto , com o comando .
Na quarta linha, dizemos que o eixo Y do gráfico corresponde à variável de projeto , com o comando .
Bora rodar o programa pra ver as curvas de nível:
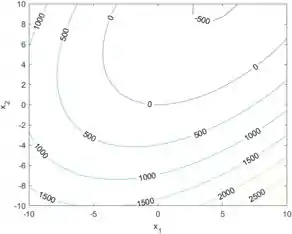
Note que é o mesmo desenho que temos no plano no gráfico da superfície, do passo 3.
Repare que as curvas com menor estão no canto superior direito do gráfico. Quanto mais afastado do canto superior direito, maior a intensidade de .
A curva de menor intensidade mostrada no gráfico é Isto significa que as coordenadas e que dão o mínimo estão no interior dessa curva e que a energia potencial mínima é pelo menos , mas pode assumir valores menores ainda.
Podemos ver as coordenadas de certos pontos ao clicar sobre o ponto no gráfico. No gráfico acima, o ponto com menor que encontrei tem coordenadas e , que dão um .
Passo 5
Encontrei dois pontos diferentes em cada gráfico, pois é muito difícil detectar o mínimo de uma função olhando somente as figuras. A análise dos gráficos serve apenas para termos uma noção de onde se localiza o ponto de mínimo. Na minha busca, com certeza deixei passar algum ponto com energia potencial menor.
Por isso, vamos usar o para encontrar o ponto de mínimo de maneira mais precisa (e responder à letra b do exercício).
Antes de implementar o , vamos relembrar como ele é:
Precisamos fornecer a ela no mínimo duas entradas:
- uma função representando a função objetivo;
- um vetor contendo um “chute” inicial das variáveis de projeto.
A saída de é um vetor contendo os valores das variáveis de projeto que minimizam a função objetivo.
Vamos criar uma nova função no MATLAB para representar a função objetivo . Abra um script novo e digite:

Chamei a função que contém a função objetivo de , mas você pode chamar do que quiser. tem como entrada o vetor , que tem dois elementos contendo as variáveis de projeto do problema de otimização: e . A saída de é a variável , que é a energia potencial que queremos minimizar.
Repare que tive que entrar novamente com as constantes da função , listadas no passo 1.
Após criar um script com a função objetivo, vamos implementar a . Em um novo script, salvo na mesma pasta onde está o script da função , digite as linhas de código:

Na primeira linha, entramos com o “chute” inicial das variáveis de projeto e , armazenado no vetor . O enunciado pediu para adotarmos .
Na segunda linha, usamos . Para indicar a função objetivo em , usamos o nome da função criada com a função objetivo com um na frente. Por isso a primeira entrada de , neste caso, é (caso tenha dado um nome diferente, não esqueça de trocar!). O algoritmo de otimização por trás de vai procurar o mínimo da função objetivo, isto é, o menor valor possível de , partindo de .
A saída de é o vetor , de dois elementos, com os valores de que dão o menor possível.
A terceira linha calcula o valor de usando a função , tendo como entrada o vetor dado por . Desta forma, encontramos a energia potencial mínima.
Vamos executar o programa e ver qual o ponto de mínimo que o nos dá:

Encontramos que a energia potencial mínima é e ela ocorre em e . Até que não tá tão longe do ponto que encontrei na superfície, né?
Resposta
A energia potencial mínima é e ela ocorre em e .
Exercício Resolvido #6
“UFRJ – Computação Científica – Lista 3”
Dados os pontos experimentais:
![]()
Ajuste os coeficientes () de uma reta () aos dados experimentais.
Passo 1
O enunciado nos dá alguns pontos experimentais e pede para encontrarmos uma equação da reta que corresponda aos dados. Para isto, faremos o que chamamos de “ajuste de dados” para encontrar os coeficientes e da reta.
Normalmente, quando temos pontos com coordenadas , para encontrarmos o polinômio de grau que melhor represente esse conjunto de pontos, minimizamos o erro quadrático médio :
Para o exercício, como queremos ajustar uma reta tendo pontos, temos e o erro quadrático médio torna-se:
Para ajustar a reta aos pontos, precisamos minimizar , logo, trata-se de um problema de otimização. Vamos identificar a função objetivo e as variáveis de projeto:
- “O que eu quero minimizar?”: queremos minimizar o erro quadrático médio , logo, a função objetivo é:
- “O que eu quero minimizar depende de quê?”: depende dos pontos experimentais, dados pelo enunciado, e dos coeficientes e , que são desconhecidos e queremos determinar de forma que o erro seja mínimo. Logo, as variáveis de projeto são os coeficientes da reta e .
Resumindo, queremos encontrar os coeficientes da reta que resultem em uma reta o mais próxima possível dos dados experimentais. Para encontrar esses coeficientes usaremos a função , pois precisamos minimizar o erro quadrático médio para determinar a equação da reta.
Passo 2
Antes de partir para o MATLAB, vamos relembrar como é a função :
Precisamos fornecer a ela no mínimo duas entradas:
- uma função representando a função objetivo;
- um vetor contendo um “chute” inicial das variáveis de projeto.
A saída de é um vetor contendo os valores das variáveis de projeto que minimizam a função objetivo.
Vamos começar criando a função representando a função objetivo. Em um novo script do MATLAB, crie uma função com dois vetores, e , contendo os dados experimentais:

Eu chamei a função de , mas você pode chamar como quiser. Ela tem como entrada um vetor de dois elementos chamado , representando as variáveis de projeto (os coeficientes e ), e como saída a variável , que será o erro quadrático médio, que queremos minimizar.
Abaixo dos vetores x e y, entre com a função objetivo. Digite as seguintes linhas de código:
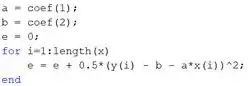
Na primeira linha, dizemos que o primeiro elemento do vetor é a variável , representando o coeficiente que multiplica o na equação da reta , isto é, o coeficiente angular.
Na segunda linha, dizemos que o segundo elemento do vetor é a variável , representando o coeficiente que está sozinho na equação da reta , isto é, o coeficiente linear.
Na terceira linha, criamos uma variável . Ela vai armazenar o erro quadrático médio, que queremos minimizar. Como o erro quadrático é calculado usando um somatório, usamos um laço para implementá-lo no MATLAB.
A partir da quarta linha, temos o laço para entrarmos com a função objetivo. Na quarta linha, inicia-se o laço , definindo uma variável de controle que vai de ao número de elementos do vetor (que é e é calculado usando a função , que retorna o número de elementos de um vetor).
Na quinta linha, calculamos o erro quadrático . A variável é atualizada a cada iteração, somando o valor obtido na iteração atual com o valor obtido na iteração anterior. Por isso temos na quinta linha e tivemos que definir antes do laço , para não termos problemas com a primeira iteração ().
Na sexta linha, encerra-se o laço .
No final, a função ficou assim:

Passo 3
Após criar um script com a função objetivo, vamos implementar a . Em um novo script, salvo na mesma pasta onde está o script da função , digite as linhas de código:
![]()
Na primeira linha, entramos com o “chute” inicial do vetor , armazenado na variável . Escolhi , mas você pode adotar outros valores.
Na segunda linha, usamos . Para indicar a função objetivo em , usamos o nome da função criada com a função objetivo com um na frente. Por isso a primeira entrada de , neste caso, é (caso tenha dado um nome diferente, não esqueça de trocar!). O algoritmo de otimização por trás de vai procurar o mínimo da função objetivo, isto é, o menor valor possível do erro quadrático médio , partindo de .
A saída de é vetor com os coeficientes da reta e que dão o menor erro possível.
Vamos rodar o programa e ver o que o retorna pra gente:

Temos que os coeficientes da reta que dão o melhor ajuste para os pontos experimentais são e .
Passo 4
Uma forma legal de visualizar o resultado é plotarmos a reta com os coeficientes encontrados junto com os dados experimentais.
No script do MATLAB onde você implemetou o , digite as linhas de código.
![]()
Nas duas primeiras linhas, entramos com os dados experimentais dados no enunciado, em forma de vetores.
Na terceira linha, usando o vetor , calculamos os valores de usando a equação da reta com os coeficientes dados pelo . O resultado é armazenado no vetor .
Em seguida, adicione o comando:
![]()
Ele gera um gráfico dos dados experimentais junto com a reta obtida a partir da otimização. O primeiro conjunto pede ao MATLAB para plotar o vetor em função do vetor (os dados experimentais), representando os pontos por bolinhas. O segundo par plota a reta obtida a partir da otimização.
Executando o programa, temos:
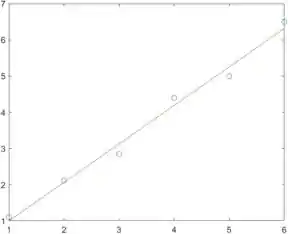
Note como a reta e os dados experimentais estão bem próximos, indicando que a nossa otimização funcionou.
Resposta
Os coeficientes da reta que dão o melhor ajuste para os pontos experimentais são e .
Exercício Resolvido #7
“Adaptado de An Engineer’s Guide to MATLAB® - With Applications from Mechanical, Aerospace, Electrical, Civil, and Biological Systems Engineering, de Edward B. Magrabet al, 3ª edição, 2011. Exercício 13.1, p. 752”
Considere o mecanismo de dois pares de barras, mostrado abaixo:

Os elos e têm o mesmo comprimento e os elos e têm o mesmo comprimento . A junta é uma junta fixa, e as juntas e são conexões por pino em duas corrediças que se movem sem atrito ao longo de uma linha horizontal. O mecanismo é submetido a três forças externas. Elas são as forças verticais e nas juntas e , respectivamente, e uma força horizontal na junta . Assume-se que as barras estavam alinhadas e esticadas ao longo de uma linha horizontal antes da aplicação das cargas. Também se assume que o peso do mecanismo é desprezível. O equilíbrio do mecanismo submetido às cargas aplicadas é obtido minimizando a função de energia potencial:
- Plote a superfície e as curvas de nível da função;
- Use com ponto inicial radianos para encontrar a energia potencial mínima.
Passo 1
O enunciado nos dá uma função e pede para que encontremos o mínimo dela usando dois métodos.
A primeira coisa que devemos entender bem antes de atacar o exercício é qual é o problema de otimização. Para isto, devemos ter bem claro:
- “O que eu quero minimizar?”, definindo a função objetivo;
- “O que eu quero minimizar depende do quê?”, definindo as variáveis de projeto.
O que queremos minimizar é a energia potencial do mecanismo composto por dois pares de barras, representada pela função dada no enunciado:
Logo, a energia potencial do sistema é minha função objetivo.
A função objetivo depende dos ângulos e e de algumas constantes, como o comprimento das barras e as cargas às quais o mecanismo é submetido, dadas pelo enunciado:
Os ângulos e são as variáveis de projeto. Em outras palavras, queremos encontrar quanto e devem valer para que a energia potencial seja a menor possível.
Usaremos dois métodos para encontrar os ângulos e que minimizam :
- Gerando a superfície e a curvas de nível: usaremos as funções e para gerar os gráficos;
- Usando , com um chute inicial radianos.
Passo 2
Vamos começar pela letra a. Em um novo script, entre as constantes listadas no passo 1:

Perceba que converti as forças de para , multiplicando-as por .
Em seguida, vamos criar dois vetores, e , representando uma faixa de valores que e podem assumir:
![]()
Os vetores e vão de a , com um passo de . Eles servirão para criar os eixos X e Y dos gráficos da superfície e das curvas de nível pedidos na letra a.
Para podermos usar as funções e do MATLAB, devemos criar matrizes a partir dos vetores e , as quais contêm as coordenadas dos vetores. Faremos isso usando a função :
![]()
A função pega os vetores e , que têm elementos, e cria duas matrizes quadradas e , de tamanho . Cada linha da matriz é o vetor , repetido vezes. Já cada coluna da matriz é o vetor , também repetido vezes.
A função serve para auxiliar na criação de gráficos em três dimensões. A matriz será o eixo X do gráfico da superfície e das curvas de nível da função . Já a matriz será o eixo Y.
O eixo Z dos gráficos será a energia potencial. Por isso temos que criar uma matriz de tamanho com os resultados de para cada elemento das matrizes e . Digite no MATLAB a equação da energia potencial dada pelo enunciado, substituindo e pelas matrizes e :
![]()
Perceba que usei os três pontos (...) para quebrar a linha de código em duas, para que a equação da energia potencial coubesse toda no meu script, sem ter que usar uma barra de rolagem para vê-la por inteiro.
Passo 3
Após ter criado as matrizes , e , podemos gerar os gráficos pedidos na letra a. Vamos começar com a superfície da função , que será gerada usando a função do MATLAB. A função tem a sintaxe:
A plota uma superfície tridimensional com as curvas de nível abaixo dela. Ela gera um gráfico 3D com os valores da matriz no eixo X, da matriz no eixo Y e da matriz no eixo Z.
Para gerar a superfície da função , adicione no script as seguintes linhas de código:

Na primeira linha, pedimos ao MATLAB para gerar uma figura com o comando , para termos o gráfico da superfície em uma janela diferente do gráfico das curvas de nível.
Na segunda linha, o comando cria a superfície da energia potencial, tendo no eixo X, no eixo Y e no eixo Z.
Na terceira linha, o comando interpola as cores do gráfico, de forma que a superfície fica sem a malha, tendo um gradiente de cores bem bonito. Você vai ver mais pra baixo, quando gerarmos o gráfico.
Na quarta linha, o comando faz com que o gráfico tenha uma barra de cores indicando a intensidade da energia potencial.
Na quinta linha, dizemos que o eixo X do gráfico corresponde à variável de projeto , com o comando .
Na sexta linha, dizemos que o eixo Y do gráfico corresponde à variável de projeto , com o comando .
Finalmente, na última linha, indicamos que o eixo Z do gráfico corresponde à energia potencial, com o comando .
Colocamos a barra na frente de e para que apareçam as letras gregas e no eixo do gráfico.
Vamos executar o programa pra ver essa superfície:

Repare que logo abaixo da superfície, no plano , temos as curvas de nível da superfície.
Podemos ver as coordenadas dos pontos da superfície clicando neles. O ponto com menor que encontrei tem coordenadas , e . Contudo, eu não tenho certeza se esse realmente é o ponto de mínimo, pois é difícil encontrar o ponto exato de mínimo olhando só a superfície.
Vamos gerar as curvas de nível em um gráfico separado para ver se facilita.
Passo 4
Para gerar um gráfico de curvas de nível, usaremos a função , que tem a seguinte estrutura:
Esse comando cria um gráfico de curvas de nível, onde as isolinhas (linhas que ligam pontos de mesmo valor) correspondem aos valores da matriz . As matrizes e definem o eixo X e o eixo Y do gráfico de curvas de nível.
Para criar o gráfico de curvas de nível, digite no seu script os comandos:

Na primeira linha, pedimos ao MATLAB para criar uma segunda figura com o comando , para que o gráfico de curvas de nível seja gerado em uma janela diferente da janela onde foi plotada a superfície, no passo 3.
Na segunda linha, o comando cria o gráfico das curvas de nível da energia potencial, tendo no eixo X, no eixo Y e dando os valores para as isolinhas. As strings no final do comando () pedem ao MATLAB para mostrar o valor de cada curva do gráfico.
Na terceira linha, indicamos que o eixo X do gráfico corresponde a , com o comando . Já na quarta linha, dizemos que o eixo Y do gráfico corresponde a , com o comando .
Bora rodar o programa pra ver as curvas de nível:
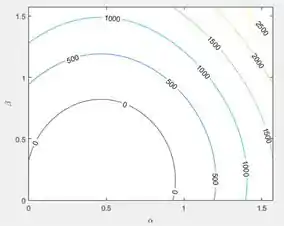
Note que é o mesmo desenho que temos no plano no gráfico da superfície, do passo 3.
Repare que as curvas com menor estão na parte inferior do gráfico. A curva de menor intensidade mostrada no gráfico é Isto significa que os ângulos e que dão o mínimo estão no interior dessa curva e que a energia potencial mínima é pelo menos , mas pode assumir valores menores ainda.
Podemos ver as coordenadas de certos pontos ao clicar sobre o ponto no gráfico. No gráfico acima, o ponto com menor que encontrei tem coordenadas , , que dão um .
Passo 5
Encontrei dois pontos com coordenadas muito próximas em cada gráfico, mas mesmo assim é muito difícil definir o mínimo de uma função olhando somente as figuras. A análise dos gráficos serve apenas para termos uma noção de onde se localiza o ponto de mínimo. Na minha busca, com certeza deixei passar algum ponto com energia potencial menor.
Por isso, vamos usar o para encontrar o ponto de mínimo de maneira mais precisa (e responder à letra b do exercício). O tem a sintaxe:
Precisamos fornecer a ele no mínimo duas entradas:
- uma função representando a função objetivo;
- um vetor contendo um “chute” inicial das variáveis de projeto.
A saída de é um vetor contendo os valores das variáveis de projeto que minimizam a função objetivo.
Vamos criar uma nova função no MATLAB para representar a função objetivo . Abra um script novo e digite:

Chamei a função que contém a função objetivo de , mas você pode chamar do que quiser. tem como entrada o vetor , que tem dois elementos contendo as variáveis de projeto do problema de otimização: e . O primeiro elemento do vetor representa e o segundo, . A saída de é a variável , que é a energia potencial que queremos minimizar.
Repare que tive que entrar novamente com as constantes da função , listadas no passo 1.
Após criar um script com a função objetivo, vamos implementar o . Em um novo script, salvo na mesma pasta onde está o script da função , digite as linhas de código:

Na primeira linha, entramos com o “chute” inicial das variáveis de projeto e , armazenado no vetor . O enunciado pediu para adotarmos .
Na segunda linha, usamos . Para indicar a função objetivo em , usamos o nome da função criada com a função objetivo com um na frente. Por isso a primeira entrada de , neste caso, é (caso tenha dado um nome diferente, não esqueça de trocar!). O algoritmo de otimização por trás de vai procurar o mínimo da função objetivo, isto é, o menor valor possível de , partindo de .
A saída de é o vetor , de dois elementos, com os valores de e que dão o menor possível.
A terceira linha calcula o valor de usando a função , tendo como entrada o vetor dado por . Desta forma, encontramos a energia potencial mínima.
Vamos executar o programa e ver qual o ponto de mínimo que o nos dá:

Encontramos que a energia potencial mínima é e ela ocorre em e . Até que deu um resultado bem pertinho dos valores que tiramos dos gráficos =D
Resposta
A energia potencial mínima é e ela ocorre em e
Exercício Resolvido #8
“Adaptado de An Engineer’s Guide to MATLAB® - With Applications from Mechanical, Aerospace, Electrical, Civil, and Biological Systems Engineering, de Edward B. Magrab et al, 3ª edição, 2011. Exercício 13.7, p. 758”
A figura abaixo mostra um sistema de molas em posição não-deformada sem cargas (linha tracejada) e em posição deformada com cargas nas juntas entre as molas (linha cheia.)
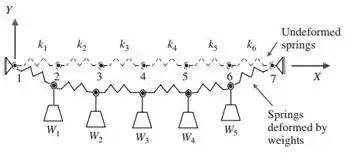
A rigidez da mola é e é definida por:
Onde é o número de cargas. O peso é definido por
O comprimento de cada mola antes da aplicação das cargas é . As coordenadas das juntas das molas (pontos ) são representadas por dez variáveis de projeto: , . Para encontrar a posição de equilíbrio, a seguinte função de energia potencial é minimizada:
Onde
Determine as posições de equilíbrio usando fminsearch, isto é, as posições das juntas para o sistema com as molas deformadas. Use o ponto inicial .
Passo 1
O enunciado nos dá uma função e pede para que encontremos o mínimo dela usando .
A primeira coisa que devemos entender bem antes de atacar o exercício é qual é o problema de otimização. Para isto, devemos ter bem claro:
- “O que eu quero minimizar?”, definindo a função objetivo;
- “O que eu quero minimizar depende do quê?”, definindo as variáveis de projeto.
O que queremos minimizar é a energia potencial do sistema de molas, representada pela função dada no enunciado:
Logo, a energia potencial do sistema é minha função objetivo.
A função objetivo depende das coordenadas das juntas das molas e de algumas constantes, como o número de cargas e o comprimento das molas relaxadas, dadas pelo enunciado:
As coordenadas das juntas a são as variáveis de projeto. Em outras palavras, queremos encontrar qual a posição das juntas a que dê a menor energia potencial possível.
Passo 2
Para vermos por onde vamos começar o exercício, vamos relembrar a sintaxe de :
A função precisa de no mínimo duas entradas:
- uma função representando a função objetivo;
- um vetor contendo um “chute” inicial das variáveis de projeto.
A saída de é um vetor contendo os valores das variáveis de projeto que minimizam a função objetivo.
O vetor nos foi dado no enunciado, falta definirmos a função objetivo dada pelo enunciado no MATLAB. Vamos começar fazendo isso. Em um script novo, crie uma função chamada (ou dê o nome que você quiser), que tem como entrada um vetor de elementos, representando as variáveis de projeto.
Entre com as constantes listadas no passo 1: o número de cargas e o comprimento das molas :

Existe outra informação que podemos tirar do enunciado, principalmente da imagem: as coordenadas das juntas e . Ambas as juntas são fixas, logo, suas coordenadas não vão mudar com a adição das cargas.
Repare que o sistema de referência está bem em cima da junta na figura do enunciado, logo, as coordenadas da junta são:
Para a junta , ela se encontra exatamente sobre o eixo do sistema de referência , logo, . Já a sua coordenada em é determinada pelo comprimento das molas sem carga: entre a junta e a junta , existem molas, logo .
Digite as coordenadas das juntas e na função :

Passo 3
Tendo as coordenadas das juntas e , vamos criar dois vetores, um com as coordenadas em das juntas do sistema, e outro com a coordenada , para nos ajudarem a construir a função objetivo. Esses vetores seriam assim:
Para criar esses vetores na nossa função, vamos usar as coordenadas , , e definidas no passo anterior e o vetor , que é a entrada da função que contém as variáveis de projeto, que são as coordenadas das juntas a . O vetor é assim:
Logo, para gerar os vetor e no MATLAB, vamos usar essas duas linhas de código:
![]()
Na primeira linha de código, o primeiro elemento do vetor é , que é seguido da primeira metade de , isto é, das coordenadas em das juntas a . O último elemento de é .
Da mesma forma, na segunda linha de código, o primeiro elemento do vetor é , que é seguido da segunda metade de , isto é, das coordenadas em das juntas a . O último elemento de é .
Passo 4
Com os vetores e definidos, podemos começar a entrar com a função obejtivo:
Vamos dividir em duas partes: o primeiro somatório se refere à energia potencial elástica e o segundo, à energia potencial gravitacional. Vamos calcular cada parte separadamente e no final, as juntamos para termos .
Vamos começar pelo primeiro somatório:
Para construi-lo, vamos precisar de um laço , para calcular e para cada e somar o produto ao produto obtido com valores de anteriores. Por isso, adicione em sua função as linhas de código:

Na primeira linha de código, criamos uma variável e a fazemos igual a . É ela quem vai representar o resultado do somatório .
Na segunda linha, inicia-se o laço , com uma variável de controle que vai de a (como no somatório da energia potencial elástica).
Na terceira e na quarta linha, calculamos a rigidez e a deformação da mola . Note que usamos os vetores e criados no passo anterior para calcular , pois a deformação depende das coordenadas das juntas.
Na quinta linha, atualizamos a variável , fazendo-a igual à soma dela mesma com o produto . Desta forma, somamos ao valor de da iteração anterior, para no final, com , termos o resultado do somatório .
Passo 5
Tendo concluído a criação do primeiro somatório, vamos partir para o segundo, o da energia potencial gravitacional:
Para construi-lo, também usaremos um laço , para calcular para cada , multiplicá-lo pela coordenada da junta e somar o produto ao produto obtido com valores de anteriores. Por isso, adicione em sua função as linhas de código:

Na primeira linha de código, criamos uma variável e a fazemos igual a . É ela quem vai representar o resultado do somatório .
Na segunda linha, inicia-se o laço , com uma variável de controle que vai de a (como no somatório da energia potencial gravitacional).
Na terceira, calculamos o peso .
Na quarta linha, atualizamos a variável , fazendo-a igual à soma dela mesma com o produto . Desta forma, somamos . ao valor de da iteração anterior, para no final, com , termos o resultado do somatório .
Note que aqui usamos o vetor criado no passo 3, pois a energia potencial gravitacional depende da posição das cargas.
Após os dois laços , podemos calcular , a nossa função objetivo:
![]()
No final, a função ficou assim:

Passo 6
Após criar um script com a função objetivo, vamos implementar a . Em um novo script, salvo na mesma pasta onde está o script da função , digite as linhas de código:

Na primeira linha, entramos com o “chute” inicial das coordenadas das juntas, armazenado no vetor , fornecido pelo enunciado.
Na segunda linha, definimos uma variável por meio de , uma função que serve para mudar alguns parâmetros do algoritmo de otimização. Nesta linha, aumentamos o número de vezes que é calculado por meio da função , alterando o parâmetro . Por padrão, o MATLAB calcula a função objetivo vezes o número de variáveis de projeto (que no nosso caso é , logo, seria vezes). Contudo, esse valor não é o suficiente para o algoritmo achar um ponto de mínimo, por isso, aumentei para vezes.
O número máximo de iterações do algoritmo também foi aumentado, mexendo no parâmetro . Por padrão, o número máximo de iterações também é vezes o número de variáveis de projeto, o que também não foi o suficiente para encontrar um ponto de mínimo. Por isso, aumentei para .
Na terceira linha, usamos . Note que dessa vez ela tem três entradas: a função objetivo, o “chute” inicial e , que é a variável criada para mexer em alguns parâmetros do algoritmo de otimização. A saída de é o vetor com as posições das juntas a que dão o menor possível.
Vamos rodar o programa para ver o que o vai retornar:
![]()
Para ver qual é o valor mínimo de , acrescente no código o comando:
![]()
Com este comando, calculamos usando a função , tendo como entrada o resultado de .
Execute o programa para ver o mínimo:
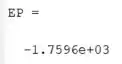
Resposta
As posições de equilíbrio das juntas para o sistema de molas é:
A energia potencial para essas coordenads é .