Funções de Transferência
Produzido por Gustavo BarbosaTeoria
Introdução
E aí, pequeno gafanhoto? Se você já passou por alguma disciplina de Controle, com certeza viu o que era uma função de transferência. Relembrando rapidamente, uma função de transferência é uma forma de representar a dinâmica de um sistema linear e invariante no tempo. Ela é a relação entre a transformada de Laplace do sinal de saída pela transformada de Laplace do sinal de entrada, com todas as condições iniciais nulas.
Para ilustrar essa definição, considere o diagrama de blocos abaixo:
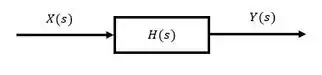
Nele, a transformada de Lapalce do sinal de entrada é representada por , já a transformada do sinal de saída é representado por . representa a função de transferência, dada por:
Funções de transferência são utilizadas na criação de controladores de sistemas como servomotores, suspensões ativas, circuitos elétricos, entre outros. Caso queira dar mais uma refrescada na memória, o Responde Aí tem um conteúdo completinho sobre Sistemas de Controle ;)
O MATLAB possui algumas funções para criar funções de transferência e modelar sinais de entrada. Na aula de hoje, você terá o prazer de conhecer algumas delas.

Criando uma função de transferência no MATLAB
No MATLAB, usamos a função para criar funções de transferência de tempo contínuo ou discreto no domínio da frequência (representado pela variável da transformada de Laplace, para tempo contínuo). Nesta aula, veremos apenas funções de transferência de tempo contínuo, que podem ser criadas no MATLAB usando com a sintaxe:
A função tem como entrada dois vetores, um contendo os coeficientes do numerador da função de transferência e outro contendo os coeficientes do denominador. retorna um objeto representando a função de transferência.
Vamos ver como a função funciona com um exemplo. Digamos que você queira entrar, no MATLAB, a função de transferência:
Em um novo script, crie dois vetores, um contendo os coeficientes do numerador e outro contendo os coeficientes do denominador:
![]()
Em seguida, entre com a função :
![]()
Utilizamos como entrada os vetores e e a função vai nos retornar a função de transferência, armazenando-a na variável .
Para ver a cara da função de transferência, rode o programa e imprima no Command Window a variável :

Bem legal, né? O MATLAB já imprime ela bonitinha pra gente e indica que representa uma função de transferência de tempo contínuo. Repare que, por padrão, o MATLAB adota a letra na transformada de Laplace.
Função de transferência e sinais de entrada
Podemos ver a resposta de um sistema, tendo criado no MATLAB sua função de transferência usando o comando , considerando alguns sinais de entrada. Nesta aula, veremos três sinais de entrada diferentes: degrau unitário, impulso e entrada arbitrária.
Para ver a resposta ao degrau unitário, utilize o comando :
Onde é a função de transferência criada usando o comando . A função com a sintaxe acima plota o gráfico da resposta ao degrau unitário.
Para vermos como o funciona, vamos usar o script da seção anterior, com a função de transferência e que, por enquanto, tem as seguintes linhas de código:

Adicione ao script o comando:
![]()
Rode o programa e você verá este lindo gráfico:
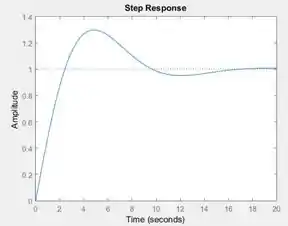
Caso você queira um degrau de amplitude em vez de , você pode multiplicar a entrada de por :
Digamos que, no nosso exemplo, você queira usar um degrau de amplitude em vez de um degrau unitário. Para ver a resposta do sistema, adicione no script a linha de código:
![]()
Rodando o programa, você terá um gráfico muito parecido com o de cima, mudando apenas a amplitude do sinal:
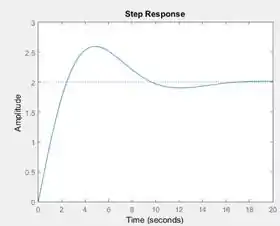
O comando também pode ter a seguinte sintaxe:
Neste formato, tem uma segunda entrada, um vetor representando o intervalo de tempo em que quero calcular a resposta ao degrau unitário. Repare que o MATLAB deu a resposta para um intervalo de , pode acontecer de eu querer ver a resposta em um intervalo de tempo específico.
Além disso, neste formato, a função me retorna um vetor contendo a resposta ao degrau para cada elemento de . Esse recurso pode ser útil caso você tenha que trabalhar com a resposta depois. Quando usamos essa sintaxe, o gráfico não é gerado automaticamente. Para vermos o gráfico da resposta ao degrau, devemos usar o comando .
Para o nosso exemplo, digamos que eu queira ver a resposta ao degrau unitário por em vez de . Para isto, eu utilizo as três linhas de código:

Na primeira linha, um vetor é criado: ele vai de a , com um passo de .
Na segunda linha, é usado comando com a sintaxe .
Na terceira linha, usamos o comando pra gerar o gráfico.
Ao rodarmos o programa, temos:
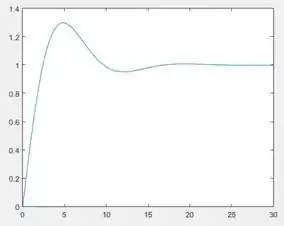
Note que esse gráfico é igualzinho ao gráfico gerado usando apenas , ele apenas vai até em vez de .
O comando para ver a resposta ao impulso tem a sintaxe igualzinha ao . A resposta ao impulso é calculada usando o comando :
Novamente, é a função de transferência criada usando o comando e, usando a sintaxe acima, plota-se automaticamente o gráfico da resposta ao impulso.
Para o nosso exemplo, adicione o comando:
![]()
Rodando o programa, você terá o seguinte gráfico:
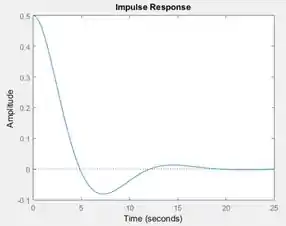
Assim como , o comando também pode ter a sintaxe , com as mesmas utilidades.
Finalmente, para uma entrada arbitrária, temos o comando:
Onde é a função de transferência criada com ; é um vetor representando a entrada arbitrária para cada elemento do vetor , que representa o tempo. O comando , com a sintaxe acima, gera o gráfico da resposta à entrada quando rodamos o programa.
Digamos que, para nosso exemplo, queremos ver qual é a resposta para a entrada em função do tempo :
No script do MATLAB onde criamos a função de transferência (armazenada na variável ), adicione os comandos:

Na primeira linha, criamos o vetor : ele vai de a, com um passo de .
Na segunda linha, calculamos para cada elemento de e armazenamos o resultado no vetor .
Na terceira linha, usamos o comando o .
Rodando o programa, temos um gráfico bem legal:

A curva vermelha é a entrada e a curva azul, a resposta do sistema a .
Assim como e , pode ser usada no formato , para armazenar a resposta do sistema no vetor . Mas, assim como os outros, com essa sintaxe, não temos o gráfico diretamente, temos que usar a função em seguida.
Vimos bastante coisa, né? Bora praticar para fixar bem esse conteúdo ;D
Função de transferência e sinais de entrada
Exercícios Resolvidos
Exercício Resolvido #1
“Adaptado de MATLAB: The Language of Technical Computing, prof. Carlos Alexandre Mello, Centro de Informática UFPE, VIISAR”
Crie no MATLAB a função de transferência:
Passo 1
O exercício pede para entrarmos no MATLAB com a função de transferência dada o enunciado. Para isto, usaremos a função do MATLAB.
Como a função de transferência é em função de e o enunciado não especifica mais nada, isso quer dizer que ela foi obtida por meio da transformada de Laplace a partir de funções no domínio de tempo contínuo.
Passo 2
Antes de começar o código, vamos relembrar a sintaxe da função :
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Abra um script novo no MATLAB e crie dois vetores, um contendo os coeficientes de e outro contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:
![]()
O vetor contém os coeficientes do numerador e o vetor , do denominador.
Passo 3
Em seguida, utilize a função para criar a função de transferência no MATLAB:
![]()
A função de transferência é armazenada na variável , isto é, é igual a .
Ao executar o programa, você terá implementado no MATLAB. Você pode vê-la pedindo ao MATLAB para imprimir no Command Window.
Resposta

Exercício Resolvido #2
“UnB – Laboratório de Análise Dinâmica Linear – Experimento 01 – primeira parte: Simulação de Sistemas Dinâmicos Lineares Visão Geral do MATLAB (2017)”
Um circuito RLC série tem a seguinte função de transferência:
Defina a função de transferência no MATLAB para os seguintes parâmetros: , e .
Passo 1
O exercício pede para definirmos no MATLAB a função de transferência de um circuito RLC. Para isto, entraremos com os parâmetros do circuito (, e ) e em seguida usaremos a função do MATLAB.
Como a função de transferência é em função de e o enunciado não especifica mais nada, isso quer dizer que ela foi obtida por meio da transformada de Laplace a partir de funções no domínio de tempo contínuo.
Passo 2
Primeiramente, vamos entrar com parâmetros do circuito RLC dados pelo enunciado. Em um novo script do MATLAB, digite:

Agora devemos criar as entradas da função para definirmos no MATLAB . Vamos relembrar a sintaxe da função :
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
No nosso script, vamos criar duas variáveis representando os coeficientes dos polinômios. Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente () ao de menor expoente (, pois ele multiplica ):
![]()
Passo 3
Em seguida, utilize a função para criar a função de transferência do circuito RLC no MATLAB:
![]()
A função de transferência é armazenada na variável , isto é, é igual a .
Ao executar o programa, você terá definido no MATLAB. Você pode vê-la pedindo ao MATLAB para imprimir no Command Window.
Resposta

Exercício Resolvido #3
“Adaptado de UnB – 107506: Laboratório de Controle de Processos. Aula: MATLAB. Prof. Eduardo Stockler Tognetti (2018) – Exercício 4”
Seja
Plote a resposta ao degrau de amplitude de .
Passo 1
O exercício pede para gerarmos o gráfico da resposta ao degrau de amplitude para uma função de transferência . Para isto, usaremos a função para criarmos no MATLAB e, em seguida, usaremos a função , que plota a resposta ao degrau de uma função de transferência.
Como é em função de e o enunciado não especifica mais nada, isso quer dizer que ela foi obtida por meio da transformada de Laplace a partir de funções no domínio de tempo contínuo.
Passo 2
Vamos relembrar a sintaxe da função :
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Precisamos criar os vetores com os coeficientes dos polinômios, mas repare que o numerador e o denominador de estão fatorizados. Logo, precisamos expandi-los (isto é, multiplicar os termos) para termos uns polinômios bem bonitos para pegar os coeficientes.
Vamos fazer isso no MATLAB mesmo. Em um script, digite as linhas de código:

Na primeira linha, criamos uma variável simbólica .
Na segunda linha, entramos com o numerador de , armazenando-o na variável .
Na terceira linha, usamos o comando do MATLAB em . Este comando multiplicará os termos de e gerará o polinômio que precisamos, armazenando-o em .
Rodando o programa, temos:
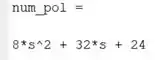
Adicione ao seu script as duas linhas de código abaixo, para fazer exatamente a mesma coisa com o denominador de :
![]()
Na primeira linha, entramos com denominado de , armazenando-o em . Em seguida, usamos em para gerar o polinômio do denominador, armazenando-o em .
Rodando o programa, temos os polinômios do numerador e do denominador de :

Passo 3
Agora que conhecemos os polinômios do numerador e do denominador de , podemos criar os vetores que servirão de entrada para .
O polinômio do numerador é . Já o polinômio do denominador é .
No nosso script, vamos criar dois vetores contendo os coeficientes dos polinômios. O primeiro vetor conterá os coeficientes do polinômio do numerador e será chamado de . O segundo vetor se chamará e terá os coeficientes do polinômio do denominador.
Ambos os vetores vão do elemento com maior expoente ( para o numerador e para o denominador) ao de menor expoente ( para o numerador e para o denominador, pois multiplicam ):
![]()
Em seguida, utilize a função para criar a função de transferência no MATLAB:
![]()
A função de transferência é armazenada na variável , isto é, é igual a .
Vamos ver a carinha dela? Rode o programa e você terá:

Passo 4
Agora que já entramos com no MATLAB, vamos ver qual é a resposta de a um degrau de amplitude . Para isto, usaremos a função , que tem a sintaxe:
A função com a sintaxe acima plota o gráfico da resposta ao degrau unitário de , que é uma função de transferência criada usando o comando .
Se quiséssemos a resposta ao degrau unitário, bastaria incluir o comando em nosso código. Contudo, queremos ver a resposta para um degrau de amplitude . Por isso, devemos multiplicar por ao utilizarmos . Isto quer dizer que você deve adicionar no script o seguinte comando:
![]()
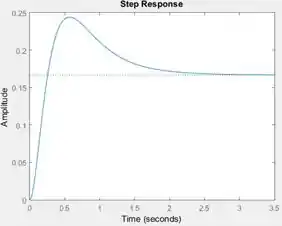
Ao rodar o programa, você terá o gráfico da resposta de a um degrau de amplitude .
Resposta
Exercício Resolvido #4
“Adaptado de UnB – 107506: Laboratório de Controle de Processos. Aula: MATLAB. Prof. Eduardo Stockler Tognetti (2018) – Exercício 4”
Seja
Plote a resposta de à entrada .
Passo 1
O exercício pede para gerarmos o gráfico da resposta à entrada de uma função exponencial para uma função de transferência . Para isto, usaremos a função para criarmos no MATLAB e, em seguida, usaremos a função , que plota a resposta a uma entrada arbitrária de uma função de transferência.
Como é em função de e o enunciado não especifica mais nada, isso quer dizer que ela foi obtida por meio da transformada de Laplace a partir de funções no domínio de tempo contínuo.
Passo 2
Primeiramente, vamos rever a sintaxe da função :
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
O polinômio do numerador de é . Já o polinômio do denominador é .
Em um novo script, vamos criar dois vetores contendo os coeficientes dos polinômios. O primeiro vetor conterá os coeficientes do polinômio do numerador e será chamado de . O segundo vetor se chamará e terá os coeficientes do polinômio do denominador.
Ambos os vetores vão do elemento com maior expoente ( para o numerador e para o denominador) ao de menor expoente ( para o numerador e para o denominador, pois multiplicam ):
![]()
Tendo criado os vetores de entrada de , podemos incluir o comando abaixo para criar a função de transferência :
![]()
A função de transferência é armazenada na variável , isto é, é igual a . Podemos conferir isso rodando o programa e pedindo ao MATLAB para imprimir no Command Window:

Passo 3
Agora que já entramos com no MATLAB, vamos ver qual é a resposta de à entrada . Para isto, usaremos a função , que tem a sintaxe:
Onde é uma função de transferência criada com ; é um vetor representando uma entrada arbitrária (pode ser qualquer expressão em função do tempo) para cada elemento do vetor , que representa o tempo. O comando , com a sintaxe acima, gera o gráfico da resposta à entrada quando rodamos o programa.
No exercício, queremos ver qual é a resposta para a entrada em função do tempo :
No nosso script, adicione os comandos:

Na primeira linha, criamos o vetor : ele vai de a, com um passo de .
Na segunda linha, calculamos para cada elemento de e armazenamos o resultado no vetor .
Na terceira linha, usamos o comando o para a função de transferência criada no passo anterior.
Ao executar o programa, você terá o gráfico da resposta de a .
Resposta
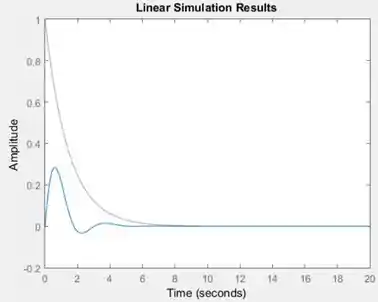
A entrada é representada pela curva vermelha.
A resposta de a é representada pela curva azul.
Exercício Resolvido #5
“Adaptado de UnB – 107506: Laboratório de Controle de Processos. Aula: MATLAB. Prof. Eduardo Stockler Tognetti (2018) – Exercício 5”
Plotar a resposta ao impulso de
Passo 1
O exercício pede para gerarmos o gráfico da resposta ao impulso de . Para isto, usaremos a função do MATLAB para criarmos a função de transferência e, em seguida, usaremos a função para ver sua resposta ao impulso.
Contudo, você deve ter reparado que tem um formato um pouco diferente do que estamos acostumados: existe um exponencial no numerador. Um exponencial no numerador de uma função de transferência representa matematicamente um atraso entre o sinal de entrada e o de saída. É uma forma de modelar matematicamente atrasos em sistemas de controle reais. Por exemplo, em um reator químico ou em aeronaves, pode haver uma demora de alguns segundos do sinal de saída, devido a atuadores ou sensores.
Normalmente, funções de transferência que modelam atrasos no sinal tem o seguinte formato:
Onde seria uma função de transferência no formato que estamos acostumados (polinômios no numerador e no denominador) e modela um atraso de segundos entre o sinal de entrada e o sinal de saída.
No exercício, temos segundos e
Veremos que, para incluirmos em uma função de transferência usando o do MATLAB, basta adicionarmos mais uma entrada em indicando o tempo de atraso .
Passo 2
Para entendermos bem como funciona esse conceito de tempo de atraso entre os sinais de entrada e de saída, vamos primeiro trabalhar somente com e ver sua resposta ao impulso.
Usaremos a função para criarmos no MATLAB, que tem a sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
O polinômio do numerador de é . Já o polinômio do denominador é .
No nosso script, vamos criar duas variáveis representando os coeficientes dos polinômios. Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente () ao de menor expoente (, pois ele multiplica ):
![]()
Tendo criado as entradas de , podemos incluir o comando abaixo para criar a função de transferência :
![]()
A função de transferência é armazenada na variável , isto é, é igual a . Podemos conferir isso rodando o programa e pedindo ao MATLAB para imprimir no Command Window:

Passo 3
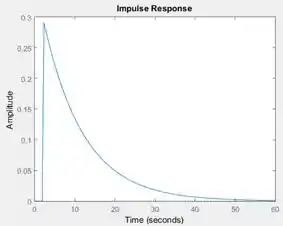
Após criarmos , vamos ver sua resposta ao impulso, sem o atraso de segundos, isto é, desconsiderando o componente . A resposta ao impulso de uma função de transferência é calculada usando o comando :
Onde é a função de transferência criada usando o comando . Usando a sintaxe acima, plota-se automaticamente o gráfico da resposta ao impulso de .
Inclua em seu script os comandos:
![]()
Na primeira linha, dizemos que o gráfico que será gerado por será a primeira figura. Incluimos esse comando para que os gráficos sem e com atraso sejam gerados em janelas diferentes e possamos compará-los.
Na segunda linha, usamos a função para vermos a resposta ao impulso de .
Vamos rodar o programa para vermos a resposta ao impulso sem o atraso de segundos:

Perceba que a curva azul já começa no instante , que é o instante quando ocorre o impulso.
Passo 4
Agora vamos incluir no sistema o atraso de s entre a entrada e a saída, isto é, vamos criar a função de transferência . Lembrando que um atraso entre o sinal de entrada e de saida pode ser modelado assim:
Para modelar um atraso de tempo em uma função de transferência, devemos incluir mais uma entrada na função , que terá o seguinte formato:
Os vetores e contêm os coeficientes dos polinômios do numerador e do denominador de .
Além dos vetores com os coeficientes dos polinômios do numerador e do denominador de , existe uma terceira entrada: . Essa terceira entrada indica que há um atraso de segundos entre o sinal de entrada e o de saída.
Para o exercício, como já criamos e com os coeficientes de no passo 2, para criarmos , vamos só adicionar ao nosso script o comando:
![]()
Com este comando, criamos a função de transferência do enunciado e a armazenamos em . Ao incluirmos como entrada, indicamos que em .
Se você rodar o programa que tem até agora e pedir para ver , você verá que é exatamente a função de transferência do enunciado:

Passo 5
Após criar , vamos ver sua resposta ao impulso. Para isto, adicione em seu script os comandos:
![]()
Na primeira linha, dizemos que o gráfico que será gerado por será a segunda figura. Na segunda linha, usamos a função para vermos a resposta ao impulso de .
Ao executarmos nosso programa, teremos dois gráficos gerados. Você pode colocá-los lado a lado para compará-los:

À esquerda, temos a Figure 1, que tem a resposta ao impulso de , isto é, sem o atraso de s.
À direita, temos a Figure 2, que tem a resposta ao impulso de , isto é, com o atraso de s. Perceba que há uma diferença de em torno de segundos entre as curvas azuis da esquerda e da direita. Isso ocorre devido ao exponencial de , que representa esse tempo de atraso.
Resposta
Exercício Resolvido #6
“Adaptado de “An Engineer’s Guide to MATLAB: With Applications from Mechanical, Aerospace, Electrical, Civil, and Biological Systems Engineering” (3ª edição), escrito por Edward B. Magrab et al. Exercício 9.8, p. 516”
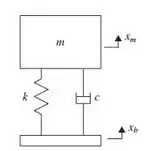
A função de transferência do sistema mecânico mostrado abaixo quando submetido a uma excitação da base é:
Considerando e , encontre a resposta do sistema a uma excitação , para .
Passo 1
O exercício pede para gerarmos o gráfico da resposta de um sistema massa-mola-amortecedor com uma base cuja excitação é dada por uma função trigonométrica. Para isto, usaremos a função para criarmos no MATLAB e, em seguida, usaremos a função , que plota a resposta a uma entrada arbitrária de uma função de transferência.
Passo 2
Em um novo script, digite os parâmetros e do sistema:
![]()
Tendo definido e , podemos entrar com no MATLAB, por meio da função , que tem como sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
O polinômio do numerador de é . Já o polinômio do denominador é .
Vamos criar dois vetores contendo os coeficientes dos polinômios. O primeiro vetor conterá os coeficientes do polinômio do numerador e será chamado de . O segundo vetor se chamará e terá os coeficientes do polinômio do denominador. Ambos os vetores vão do elemento com maior expoente ao de menor expoente:
![]()
Com os vetores de entrada de , inclua o comando abaixo para criar :
![]()
A função de transferência é armazenada na variável . Confira se você digitou tudo certinho rodando o programa e pedindo ao MATLAB para imprimir no Command Window:

Passo 3
Tendo definido no MATLAB, vamos ver qual é a resposta do sistema à excitação . Para isto, usaremos a função , que tem a sintaxe:
Onde é uma função de transferência criada com ; é um vetor representando uma entrada arbitrária (pode ser qualquer expressão em função do tempo) para cada elemento do vetor , que representa o tempo. O comando , com a sintaxe acima, gera o gráfico da resposta de à entrada .
No exercício, queremos ver qual é a resposta do sistema para a entrada em função do tempo , para :
No nosso script, adicione os comandos:

Na primeira linha, criamos o vetor : ele vai de a, com um passo de .
Na segunda linha, calculamos para cada elemento de e armazenamos o resultado no vetor .
Na terceira linha, usamos o comando o para a função de transferência criada no passo anterior. Desta forma, teremos a resposta de para a entrada .
Ao executar o programa, teremos o gráfico da resposta do sistema massa-mola-amortecedor à excitação .
Resposta
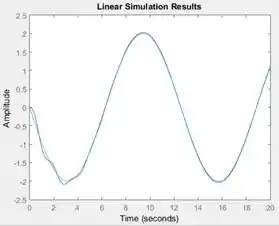
A excitação é representada pela curva vermelha.
A resposta é representada pela curva azul.
Exercício Resolvido #7
“Adaptado de “An Engineer’s Guide to MATLAB: With Applications from Mechanical, Aerospace, Electrical, Civil, and Biological Systems Engineering” (3ª edição), escrito por Edward B. Magrab et al. Exemplo 10.9, p. 557”
Considere os sistemas de primeira a quarta ordem dados por:
Plote em um mesmo gráfico as respostas ao degrau unitário de , , e e compare-as.
Passo 1
O exercício pede para plotarmos em um mesmo gráfico as resposta ao degrau unitário das funções de transferência , , e . Para isto, usaremos a função para criarmos as funções de transferência no MATLAB e, em seguida, usaremos a função , que plota a resposta ao degrau de uma função de transferência, para cada uma.
Passo 2
Primeiramente devemos criar , , e no MATLAB, usando a função , que tem como sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). Ambos os vetores vão do elemento com maior expoente ao de menor expoente.
retorna um objeto representando a função de transferência, que será armazenada em .
Vamos começar com , cujo numerador é . Já o denominador é o polinômio . Em um novo script, vamos criar duas variáveis contendo os coeficientes dos polinômios de . A primeira variável representará os coeficientes do polinômio do numerador e será chamada de . A segunda variável será um vetor chamado e terá os coeficientes do polinômio do denominador. Após criar as duas variáveis de entrada de , digite o comando :
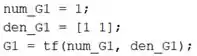
Desta forma, a função de transferência é criada e armazenada na variável Podemos ver como ficou, rodando o programa e imprimindo-o no Command Window:

Faça o mesmo procedimento para :

A variável contém o numerador de e o vetor contém os coeficientes do polinômio do denominador de . A função de transferência é criada usando e é armazenada na variável . Vamos ver como ficou :

Passo 3
Para criar , adicione em seu script o comando:
![]()
Execute o programa e veja como ficou :

Para definir , vamos criar uma “função de transferência auxiliar”, chamada de :
Temos então que
Vamos criar os vetores com os coeficientes dos polinômios do numerador e do denominador de . Vamos chamá-los de e . Logo em seguida, vamos criar usando a função :

Para calcular , adicione o comando:
![]()
Desta forma, tem essa cara:

Passo 4
Para plotar a resposta ao degrau unitário de , , e , usaremos o comando , que tem a sintaxe:
A função plota o gráfico da resposta ao degrau unitário de , que é uma função de transferência criada usando o comando .
Para termos a resposta ao degrau unitário de , , e , devemos incluir no nosso script os comandos , e assim por diante. Contudo, o enunciado pediu que plotássemos tudo no mesmo gráfico. Para fazermos isto, devemos incluir o comando após o primeiro comando que digitarmos:
O comando faz com que a curva que acabou de ser plotada não seja substituída pela próxima a ser plotada, de forma que elas apareçam juntas no gráfico.
O comando serve para criar a legenda do gráfico, para sabermos qual é a resposta de cada função de transferência.
Execute o programa e você terá o gráfico com as respostas de , , e ao degrau unitário.
Resposta
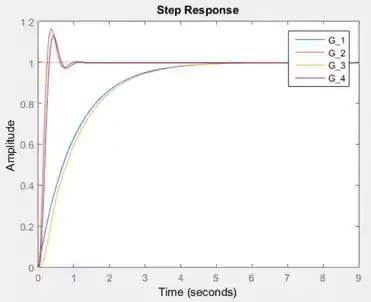
A curva azul é a resposta de ao degrau unitário.
A curva vermelha é a resposta de .
A curva amarela é a resposta de .
A curva roxa é a resposta de .
As respostas de e são similares, enquanto as respostas de e são parecidas.
Exercício Resolvido #8
“Adaptado de “An Engineer’s Guide to MATLAB: With Applications from Mechanical, Aerospace, Electrical, Civil, and Biological Systems Engineering” (3ª edição), escrito por Edward B. Magrab et al. Exercício 10.8, p. 610”
Uma suspensão automotiva é tipicamente passiva, sendo composta de molas e amortecedores. Para melhorar a suspensão de carros, sistemas de suspensão ativa têm sido propostos. Na figura abaixo, temos um modelo simplificado de uma suspensão automotiva ativa, no qual representa a entrada da superfície da estrada e é a posição vertical do compartimento dos passageiros.
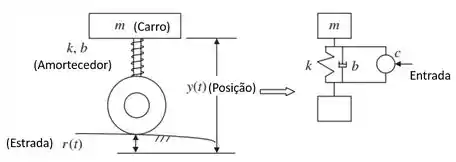
Assuma que a massa do pneu é desprezível e que a velocidade é usada no controle da suspensão ativa. A função de transferência de velocidade da estrada à posição é:
Considere , e . Plote a resposta ao degrau unitário do sistema com e sem controle ativo em um mesmo gráfico. Para considerar o controle ativo, use . Já para modelar o sistema sem o controle ativo, adote .
Passo 1
O exercício nos dá a função de transferência e pede para encontrarmos sua resposta ao degrau unitário considerando dois valores diferentes de , plotando as respostas em um mesmo gráfico.
Para isto, a função para criar e o comando para plotar o gráfico com a resposta ao degrau ficarão dentro de um laço , que atualizará e o gráfico para cada valor de .
Passo 2
O primeiro passo é digitar em um script novo os dados , , e :

Note que chamei o valor de para o modelo com suspensão ativa de .
Em seguida, crie um vetor com dois elementos: os valores 0 e . Este vetor vai nos auxiliar a montar dentro do laço :
![]()
Inicie um laço , com variável de controle , que vai de a :

Passo 3
Vamos entrar com dentro do laço , escrevendo dentro dele o comando , que tem como sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Vamos criar dois vetores, dentro do laço , contendo os coeficientes dos polinômios do numerador e do denominador de . O polinômio do numerador é e seus coeficientes serão armazenados em um vetor chamado . Já o polinômio do denominador é e seus coeficientes serão armazenados em um vetor chamado . Desta forma, o laço tem essa cara por enquanto:

Logo abaixo dos vetores, já podemos incluir o comando , para criar a variável , que contém .
Note que em vez de eu usar simplesmente , usei , indicando que na iteração vou usar o elemento na posição do vetor . Logo, na primeira iteração, e estará sendo modelada a suspensão sem controle ativo. Na segunda iteração, , sendo modelada, portanto, a suspensão com controle ativo.
Em outras palavras, com o laço de repetição , os vetores e serão atualizados a cada iteração com valores diferentes, gerando, portanto, uma função de transferência diferente a cada iteração.
Passo 4
Para gerar o gráfico com as respostas ao degrau unitário da suspensão com e sem controle ativo, utilize dentro do laço o comando , que tem a sintaxe:
A função plota o gráfico da resposta ao degrau unitário de , que é uma função de transferência criada usando o comando .
Logo, acrescente o comando dentro do laço :

Abaixo de , inclua o comando . Este comando serve para que o gráfico com a resposta ao degrau seja atualizado a cada iteração, mas sem que as curvas da iteração anterior desapareçam.
Pra finalizar, coloque logo abaixo do laço o comando:
![]()
Ele fará com que o gráfico com as respostas ao degrau tenham uma legenda, indicando qual curva representa o resultado para a suspensão sem controle ativo e com controle ativo. As legendas dentro de devem estar na ordem com que os diagramas foram criados.
Execute o programa e você terá o gráfico pedido pelo enunciado.
Resposta

A resposta do sistema sem controle ativo é representada pela curva azul. Já a resposta do sistema com controle ativo é dada pela curva vermelha.