Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Transformada Z

Ver Todos os Exercícios

Teoria

Introdução

E aí, tudo joia? Já ouviu falar de transformada Z?

“Ah, é aquele desenho onde o Goku tem que reunir as esferas do dragão para salvar o mundo, né?”

Não, você está confundindo com Dragon Ball Z!

A transformada Z é usada para analisar sinais de tempo discreto, como os gerados por radares, por exemplo. Ela é muito utilizada em no projeto de filtros e sistemas de controle digitais.

De certa forma, podemos dizer que a transformada Z é, para sinais em tempo discreto, o mesmo que a transformada de Laplace é para sinais contínuos. A transformada Z converte sinais que estão no domínio de tempo discreto n para o domínio de uma variável complexa z .

Assim como usamos a transformada de Laplace para resolver equações diferenciais, transformando-as em equações algébricas, usamos a transformada Z para transformar equações de diferenças em equações algébricas, muito mais fáceis de resolver.

“Tá, mas o que são equações de diferenças?”

Uma equação de diferenças é uma equação em tempo discreto n que relaciona a saída atual às entradas e saídas anteriores. Podemos usar equações de diferenças para modelar uma coisa bem comum no nosso dia a dia: o rendimento da poupança, que é calculado usando juros compostos. Juros compostos podem ser representados pela equação de diferenças:

y n + 1 = ( 1 + r ) y ( n )

Essa equação modela uma aplicação corrigida a juros compostos com taxa r por um período de tempo n , que pode ser em dias ou meses, por exemplo. Na poupança, o rendimento é mensal, logo, n seria a quantidade de meses.

Sabendo que a aplicação inicial é y ( 0 ) , após um mês ( n = 1 ) , você terá na poupança:

y 1 = ( 1 + r ) y ( 0 )

Já no segundo mês que você deixar seu dinheirinho rendendo na poupança, sem fazer saque algum, você terá:

y 2 = ( 1 + r ) y ( 1 )

E assim por diante.

A solução de uma equação de diferenças seria encontrar uma expressão de y ( n ) de forma que eu possa calcular a saída atual sem ter que ficar calculando a saída para cada valor de n . Por exemplo, se eu quiser saber quanto eu terei na minha poupança daqui 15 meses, eu preciso encontrar uma equação de y ( n ) de forma que basta eu dizer que n = 15 para encontrar o montante final.

Nesta aula, aprenderemos a usar função z t r a n s do MATLAB para encontrar a transformada Z de uma função f ( n ) no tempo discreto n e a usar a função i z t r a n s para encontrar a inversa da transformada Z de uma função F ( z ) , em função do número complexo z . Ao final, veremos como solucionar uma equação de diferenças usando z t r a n s e i z t r a n s .

Então, pegue a sua nuvem voadora e venha aprender mais essas funções do MATLAB com a gente!

Transformada Z de uma função f(n)

A função z t r a n s do MATLAB tem a estrutura:

F = z t r a n s ( f )

Ela retorna a transformada Z da função f , armazenando-a na variável F .

Digamos que você tenha a função f n = 2 n + 2 n e queira encontrar a sua transformada Z usando o MATLAB. Em um script novo, defina que n é uma variável simbólica e crie a função f n = 2 n + 2 n :

Vamos aplicar z t r a n s em f   :

Vamos rodar o programa e pedir para o MATLAB mostrar o resultado no Commad Window:

Temos que a transformada Z de f n = 2 n + 2 n é:

F z = 2 z z - 1 2 + z z - 2

Repare que não precisamos informar que a função de entrada f era em função da variável independente n , nem que queríamos que saída F fosse em função de z . É que, por padrão, quando usamos z t r a n s , o MATLAB considera que f depende de uma variável n e que a variável da transformada F é z . Você pode alterar isso adicionando mais entradas à função z t r a n s :

F = z t r a n s ( f , v a r _ i n d e p e n d e n t e , v a r _ z t r a n s   )

Com este comando, dizemos que a função f tem como variável independente o que pusermos no lugar de v a r _ i n d e p e n d e n t e . A transformada F gerada pelo MATLAB será em função do que pusermos no lugar de v a r _ z t r a n s .

Por exemplo, digamos que você queira encontrar a transformada Z da função:

f m = e m + n

Sendo que m é a variável independente de f ( m ) .

Além disso, você quer que a transformada Z de f ( m ) seja em função de y . Por isso, você terá que usar a função z t r a n s no MATLAB como no print abaixo:

Na primeira linha, criamos as variáveis simbólicas m , n e y .

Na segunda linha, criamos a função f m = e m + n .

Na terceira linha, usamos z t r a n s ( f , m , y ) para encontrar a transformada Z de f . Perceba que no lugar de v a r _ i n d e p e n d e n t e , coloquei m ; e que no lugar de v a r _ z t r a n s , coloquei y . Isto quer dizer que a saída F será em função de y .

Rodando o programa, temos:

Inversa da transformada Z de uma função F(z)

Digamos que agora você tem uma função no domínio da frequência z e quer encontrá-la no domínio do tempo discreto n . Você pode usar a função do MATLAB i z t r a n s , que calcula a inversa da transformada Z de uma função. Ela tem o formato:

f = i z t r a n s ( F )

Ela retorna a inversa da transformada Z da função F , armazenando-a na variável f .

Bora ver um exemplo. Temos a seguinte função no domínio de z :

F z = 2 z z - 1 2 + z z - 2

E queremos encontrá-la no domínio do tempo discreto n usando o MATLAB. Para isso, digite em um novo script as linhas de código:

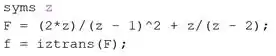
Na primeira linha, definimos a variável simbólica z .

Na segunda linha, entramos com a função F z = 2 z z - 1 2 + z z - 2 .

Na terceira linha, aplicamos i z t r a n s ( F ) para encontrar a inversa da transformada Z de F .

Rodando o programa, temos como resultado:

Temos que a inversa da transformada Z de F z = 2 z z - 1 2 + z z - 2   é f n = 2 n + 2 n . Reparou que é o mesmo exemplo da seção anterior? =)

Assim como na função z t r a n s , por padrão, em i z t r a n s , o MATLAB considera que f depende de uma variável independente n e que a variável da transformada F é z . Você também pode alterar isso adicionando mais entradas à função i z t r a n s :

f = i z t r a n s ( F , v a r _ i n d e p e n d e n t e , v a r _ i n v _ z )

Com este comando, dizemos que a função F tem como variável independente o que pusermos no lugar de v a r _ i n d e p e n d e n t e . A inversa da transformada Z f gerada pelo MATLAB será em função do que pusermos no lugar de v a r _ i n v _ z .

Resolvendo equações de diferenças usando transformada Z

Vimos como usar z t r a n s em funções f ( n ) e como usar i z t r a n s em funções F ( z ) . Agora vamos ver como usamos a transformada Z para resolver equações de diferenças. Lembram daquela equação de diferenças do começo da aula, dos juros compostos? Essa aqui:

y n + 1 = ( 1 + r ) y ( n )

Vamos encontrar uma solução para y ( n ) usando as funções z t r a n s e i z t r a n s . Primeiramente, vamos entrar com a equação de diferenças em um novo script do MATLAB:

Na primeira linha, definimos as variáveis simbólicas r e y ( n ) (indicamos que y é em função de n ).

Na segunda linha, dizemos ao MATLAB para assumir (função a s s u m e ( ) ) que a variável simbólica n é maior ou igual a zero ( n > = 0 ) e que ela é um número inteiro (pois falaremos apenas em “um mês”, “dois meses”, etc, e não consideraremos “um mês e meio”, por exemplo), usando o comando i n ( n , ' i n t e g e r ' ) .

Na terceira linha, dizemos ao MATLAB para assumir (função a s s u m e ( ) ) que a variável simbólica r é maior que zero ( n > 0 ) e que ela é um número real (pois trata-se da taxa de juros, que pode ser um número “quebrado”), usando o comando i n ( n , ' r e a l ' ) .

Na quarta linha, entramos com a equação de diferenças na variável e q n , mas dando uma reformuladinha nela, jogando todos os termos para a esquerda e dizendo que ela é igual a 0 .

Vamos aplicar z t r a n s em e q n para transformar a equação de diferenças em uma equação algébrica, armazenada em Z T :

Vamos ver como ficou? Rode o programa e peça ao MATLAB para imprimir no Command Window a variável Z T :

Perceba que o MATLAB usa z t r a n s ( y ( n ) , n , z ) em alguns elementos de Z T , que tem exatamente a mesma estrutura da função z t r a n s . Essa expressão representa a transformada Z de y ( n ) e pode ser substituída por Y ( z ) . Logo, o resultado seria assim:

z Y z - z y 0 - r + 1 Y z = 0

Esse Z T ficou meio comprido, né? Podemos substituir z t r a n s ( y ( n ) , n , z ) por Y , representado Y ( z ) , usando o comando s u b s :

Primeiramente, devemos criar mais duas variáveis simbolicas: z e Y . Em seguida, usamos a função s u b s para pedir ao MATLAB que substitua em Z T a expressão z t r a n s y n , n , z por Y . O resultado da substituição é armazenado em Z T , ficando no lugar aquela expressão comprida que vimos.

Após a substituição, Z T fica assim:

Bem mais compacto, né?

Para encontrar y ( n ) , precisamos encontrar Y ( z ) para daí aplicar nela a inversa da tranformada Z. Em Z T , a variável Y representa Y ( z ) e podemos usar a função s o l v e do MATLAB para encontrá-la. Adicione em seu código:

Com este comando, a função s o l v e resolve a equação Z T para a variável Y e armazena a solução em Z . Na prática, isolamos Y na equação com este comando e Z passa a representar Y ( z ) . Rodando o programa, temos que Z é igual a:

Isto quer dizer que:

Z = Y z = - z y ( 0 ) r - z + 1

Para encontrar y ( n ) , aplicamos a inversa da transformada Z em Y ( z ) , isto é, usamos i z t r a n s em Z :

O resultado é armazenado em y . Na prática, y = y ( n ) , logo, quando rodarmos o programa, encontraremos y ( n ) .

Na segunda linha, usamos o comando s i m p l i f y do MATLAB para deixar a expressão que obteremos de y mais bonitinha e compacta. O resultado de simplify é armazenado em y , substituindo o valor anterior de y .

Rodando o programa, temos:

Logo, para encontrarmos quanto teremos na poupança em um determinado mês, sabendo o valor inicial y ( 0 ) da aplicação, basta substituir n na equação abaixo pelo número de meses que o dinheiro ficou rendendo na poupança:

y n = r + 1 n y ( 0 )

Ufa! Vimos bastante coisa nessa aula! Bora praticar para fixar bem o conteúdo =)

Transformada Z de uma função f(n)

Inversa da transformada Z de uma função F(z)

Resolvendo equações de diferenças usando transformada Z

Exercícios Resolvidos

Exercício Resolvido #1

“Elaboração Própria”

Usando o MATLAB, calcule a transformada Z de f ( n ) = s i n ( w n ) .

Passo 1

O exercício pede para encontrarmos a transformada Z da função f ( n ) = s i n w n usando o MATLAB. Logo, usaremos a função z t r a n s ( ) neste exercício.

Como o enunciado não especificou nada, consideraremos que a variável independente de f ( n ) é n e que a transformada Z da função será em função de z , que é o padrão adotado pelo MATLAB. Em outras palavras, a transformada Z de f ( n ) será representada por F ( z ) .

Passo 2

Antes de partirmos para o MATLAB, vamos relembrar como é a função z t r a n s . A função z t r a n s do MATLAB tem a estrutura:

F = z t r a n s ( f )

Ela retorna a transformada Z da função f , armazenando-a na variável F . Como não tem mais nenhuma entrada em z t r a n s além de f , o MATLAB assumirá que a variável independente de f é n e fará que a transformada Z F seja em função de z .

Em um novo script do MATLAB, entre com a função f ( n ) = s i n ( w n ) :

Na primeira, definimos duas variáveis simbólicas: w e n .

Na segunda linha, entramos com a função f ( n ) = s i n ( w n ) , que é armazenada na variável f .

Passo 3

Após ter entrado com f ( n ) , vamos usar z t r a n s para encontrar a transformada Z de f :

A transformada Z de f é armazenada na variável F .

Rode o programa para ver como fica F :

Resposta

A transformada Z de f ( n ) = s i n ( w n ) é:

F z = z sin ⁡ w z 2 - 2 z cos ⁡ w + 1

Exercício Resolvido #2

“Elaboração Própria”

Usando o MATLAB, calcule a transformada Z de um degrau unitário u ( n ) .

Passo 1

O exercício pede para encontrarmos a transformada Z, usando o MATLAB, de uma função muito utilizada na área de controle: a função degrau unitário no tempo discreto.

Para criarmos a função degrau unitário no MATLAB, usaremos a função h e a v i s i d e ( ) . Se essa for a primeira vez que você vê essa função, não se preocupe, vamos ver direitinho como ela funciona. Ao final, usaremos a função z t r a n s ( ) para encontrar a transformada de u ( n ) .

Como o enunciado não especificou nada, consideraremos que a variável independente de u ( n ) é n e que a transformada Z dela será em função de z , que é o padrão adotado pelo MATLAB. Em outras palavras, a transformada Z de u ( n ) será representada por U ( z ) .

Passo 2

Para criarmos o degrau unitário u ( n ) no MATLAB, usaremos a função h e a v i s i d e , que tem a estrutura:

u = h e a v i s i d e ( n )

Ela cria um degrau unitário e o armazena em u : quando n   <   0 , u = 0 . Se n = 0 , u = 1 / 2 . Finalmente, para n >   0 , u = 1 .

Em um script novo, digite as três linhas de código:

Na primeira linha, criamos a variável simbólica n .

Na segunda linha, assumimos que n   >   0 , para que o degrau unitário u , definido logo abaixo, seja igual a 1 .

Na terceira linha, usamos a função h e a v i s i d e para criar o degrau unitário, que é armazenado em u . Como assumimos que n > 0 , se você rodar o programa e pedir pra ver u , você verá que:

Passo 3

Após criar o degrau unitário, podemos achar sua transformada Z usando o comando z t r a n s , que tem a estrutura:

F = z t r a n s ( f )

Ele retorna a transformada Z da função f , armazenando-a na variável F . Como não tem mais nenhuma entrada em z t r a n s além de f , o MATLAB assumirá que a variável independente de f é n e fará que a transformada Z F seja em função de z .

Adicione ao seu script o comando:

Ele vai calcular a transformada Z de u e vai armazenar o resultado em U .

Vamos ver a carinha de U ? Rode o programa e você terá:

Resposta

A transformada Z de u ( n ) é:

U z = z z - 1

Exercício Resolvido #3

“Elaboração Própria”

Usando o MATLAB, calcule a inversa da transformada Z de

F z = z ( z - a ) ( 1 - a z )

Passo 1

O exercício pede para encontrarmos a inversa da transformada Z F ( z ) = z / [ ( z - a ) ( 1 - a z ) ] usando o MATLAB. Logo, usaremos a função i z t r a n s ( ) neste exercício.

Como o enunciado não especificou nada, consideraremos que a variável independente de F ( z ) é z e que a sua inversa será em função de n , que é o padrão adotado pelo MATLAB. Em outras palavras, a inversa da transformada Z F ( z ) será representada por   f ( n ) .

Passo 2

Antes de partirmos para o MATLAB, vamos relembrar como é a função i z t r a n s . A função i z t r a n s do MATLAB tem a estrutura:

f = i z t r a n s ( F )

Ela retorna a inversa da transformada Z de F , armazenando-a na variável f . Como não tem mais nenhuma entrada em i z t r a n s além de F , o MATLAB assumirá que a variável independente de F é z e fará que a inversa da transformada Z f seja em função de n .

Em um novo script do MATLAB, entre com a função F ( z ) dada no enunciado:

Na primeira linha, criamos duas variáveis simbólicas: a e z .

Na segunda linha, dizemos ao MATLAB para assumir que a é diferente de 0 (isso simplifica a resposta no final).

Na terceira linha, entramos com a função F ( z ) dada pelo enunciado, armazenando-a na variável F .

Passo 3

Após ter entrado com F ( z ) , vamos usar i z t r a n s para encontrar a inversa da transformada Z de F :

A inversa da transformada Z de F é armazenada na variável f .

Rode o programa para ver qual é a cara de f :

Nossa, que coisa feia! Adicione em seu programa o comando s i m p l i f y , para dar uma enxugada nesse f :

Com esta linha de código, o MATLAB vai simplicar f e armazenar a resposta em f , substituindo a expressão anterior.

Ao executar o programa novamente, temos:

Resposta

A inversa da transformada Z de F ( z ) = z / [ ( z - a ) ( 1 - a z ) ] é

f n = 1 a n - a n a 2 - 1

Exercício Resolvido #4

“Elaboração Própria”

Supondo que um casal de coelhos precisa de um ano para amadurecer e gerar filhotes e que eles geram um casal de filhotes a cada ano, a população de coelhos p ( n ) no ano n é descrita pela equação das diferenças:

p ( n + 2 )   =   p ( n + 1 )   +   p ( n )

Encontre p ( n ) para determinar qual será a população de coelhos em 15 anos. Considere p ( 0 ) = 2 e p ( 1 ) = 4 .

Passo 1

O exercício pede para encontrarmos a solução p ( n ) de uma equação de diferenças, que representa a população de coelhos no ano n . Para encontrarmos p ( n ) , usaremos a transformada Z. Primeiramente, aplicaremos a função z t r a n do MATLAB na equação das diferenças para encontrarmos a transformade Z de p ( n ) . Como o enunciado não especificou nada, consideraremos que a variável independente das transformadas Z é z , que é o padrão do MATLAB. Logo, a transformada Z de p ( n ) será P ( z ) .

Após encontrarmos P ( z ) , vamos aplicar i z t r a n s para encontrar a inversa da transformada Z, isto é, p ( n ) , que é a solução da equação das diferenças. Conhecendo p ( n ) , calcularemos a população de coelhos daqui a 15 anos fazendo n = 15 .

Passo 2

Vamos começar entrando com a equação de diferenças no MATLAB. Em um script novo, digite as linhas de código:

Na primeira linha, definimos a variável simbólica p ( n ) (indicamos que p é em função de n ).

Na segunda linha, dizemos ao MATLAB para assumir (função a s s u m e ( ) ) que a variável simbólica n é maior ou igual a zero ( n > = 0 ) e que ela é um número inteiro (pois falaremos apenas em “um ano”, “dois anos”, etc, e não consideraremos “um ano e meio”, por exemplo), usando o comando i n ( n , ' i n t e g e r ' ) .

Na terceira linha, entramos com a equação de diferenças na variável e q n , mas dando uma reformuladinha nela, jogando todos os termos para a esquerda e dizendo que ela é igual a 0 .

Passo 3

Com a equação de diferenças no MATLAB, podemos usar a função z t r a n s para calcular a transformada Z dela. Lembrando que z t r a n s tem como estrutura:

F = z t r a n s ( f )

Ela retorna a transformada Z da função f , armazenando-a na variável F . Quando não tem mais nenhuma entrada em z t r a n s além de f , o MATLAB assume que a variável independente de f é n e fará que a transformada Z F seja em função de z .

Acrescente em seu programa o comando abaixo para calcular a transformada Z de e q n :

O resultado é armazenado em E .

Vamos ver como ficou E ? Rodando o programa que fizemos até agora, temos:

Percebe que tem um termo aí que aparece umas três vezes? z t r a n s ( p ( n ) ,   n ,   z ) tem exatamente a mesma estrutura da função z t r a n s e representa a transformada Z de p ( n ) , podendo ser substituído por P ( z ) . No caso, chamaremos P ( z ) só de P .

Adicione os comandos abaixo em seu programa para fazer a substituição:

Primeiramente, devemos criar mais duas variáveis simbolicas: z e P . Em seguida, usamos a função s u b s para pedir ao MATLAB que substitua em E a expressão z t r a n s ( p ( n ) ,   n ,   z ) por P . O resultado da substituição é armazenado em E , ficando no lugar daquela expressão comprida que vimos.

Após a substituição, E fica assim:

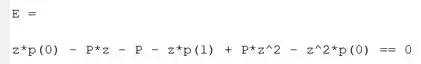
Bem mais bonitinha, né? E tem mais coisa pra substituir aí. O enunciado disse para considerarmos p ( 0 ) = 2 e p 1 = 4 . Para fazer as substituições, adicione ao seu programa a linha de código:

Com este comando, substituímos p ( 0 ) por 2 e p ( 1 ) por 4 em E e armazenamos a nova expressão em E , no lugar daquele E mostrado no print acima. Executando o programa, podemos ver como E está agora:

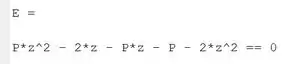
Passo 4

Para encontrar p ( n ) , precisamos encontrar P ( z ) para daí aplicar nela i z t r a n s , para termos a inversa da tranformada Z. Em E , a variável P representa P ( z ) e podemos usar a função s o l v e do MATLAB para encontrá-la. Adicione em seu código:

Com este comando, a função s o l v e resolve a equação E para a variável P e armazena a solução em P , atualizando seu valor. Na prática, isolamos P na equação com este comando e P passa a representar a expressão algébrica de P ( z ) . Rodando o programa, temos que P é igual a:

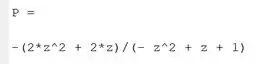
Quer dizer que:

P z = - 2 z 2 + 2 z - z 2 + z + 1

Para encontrarmos p ( n ) , devemos aplicar a inversa da transformada Z em P ( z ) , isto é, usar a função i z t r a n s do MATLAB em P . A função i z t r a n s tem a estrutura:

f = i z t r a n s ( F )

Ela retorna a inversa da transformada Z de F , armazenando-a na variável f . Quando não tem mais nenhuma entrada em i z t r a n s além de F , o MATLAB assume que a variável independente de F é z e fará que a inversa da transformada Z f seja em função de n .

Para encontrar p ( n ) , entre o comando:

Com este comando, o MATLAB calcula a inversa da transformada Z de P e armazena o resultado em p , atualizando seu valor. p é a solução da equação de diferenças e representa a população de coelhos em função de n anos.

Rodando o programa, temos que p é igual a:

Que expressão comprida, né? Tive que deixar a fonte bem pequenininha pra caber na página.

Passo 5

Queremos encontrar a população de coelhos em 15 anos. Para isto, substituiremos n por 15   em p , usando o comando:

O resultado é armazenado na variável p 15 , representando p ( 15 ) .

Se rodarmos o programa, teremos uma expressão gigantesca que não nos dará diretamente a população de coelhos em 15 anos:

Isso acontece pois p 15 é uma variável simbólica. Para encontrarmos a população, devemos resolver cada uma das operações matemáticas de p 15 , usando o comando v p a :

Este comando aplica a função v p a em p 15 e armazena o resultado em p 15 , substituindo a expressão anterior pelo resultado das operações matemáticas. Ao rodar programa, temos:

p 15 é um número complexo, mas note que a parte imaginária é bem pequenininha, na ordem de 10 - 35 . Logo, podemos desprezar a parte imaginária e dizer que a população de coelhos daqui a 15 anos é 3194 .

Resposta

Daqui a 15 anos, a população de coelhos será de 3194 .

Exercício Resolvido #5

“Elaboração Própria”

Obtenha a resposta ao degrau unitário u n para o sistema descrito pela equação de diferenças de segunda ordem:

y n - 3 4 y n - 1 + 1 8 y n - 2 = u n

Considere as condições iniciais iguais a 0 .

Passo 1

O exercício pede para encontrarmos a resposta do degrau unitário para um sistema descrito por uma equação de diferenças de segunda ordem. A solução y da equação de diferenças representa a resposta ao degrau unitário, logo, temos que achar uma expressão para y .

Faremos isso usando a transformada Z, por isso, primeiramente, aplicaremos a função z t r a n s do MATLAB na equação de diferenças para encontrarmos a transformada de y , que indicarems por Y .

Temos que y é em função de n e, como o enunciado não especificou nada, consideraremos que a variável independente das transformadas Z é z , que é o padrão do MATLAB. Logo, a transformada Z de y ( n ) será Y ( z ) .

Após encontrarmos Y ( z ) , vamos aplicar i z t r a n s para encontrar a inversa da transformada, isto é, y ( n ) , que é a solução da equação de diferenças e a resposta ao degrau unitário.

Passo 2

Vamos começar entrando com a equação de diferenças no MATLAB. Em um script novo, digite as linhas de código:

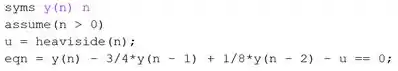
Na primeira linha, definimos as variáveis simbólicas n e y ( n ) (indicamos que y é em função de n ).

Na segunda linha, assumimos que n   >   0 , para que o degrau unitário u , definido logo abaixo, seja igual a 1 .

Na terceira linha, usamos a função h e a v i s i d e para criar o degrau unitário, que é armazenado em u . A função h e a v i s i d e tem a estrutura:

u = h e a v i s i d e ( n )

Ela cria um degrau unitário e o armazena em u : quando n   <   0 , u = 0 . Se n = 0 , u = 1 / 2 . Finalmente, para n >   0 , u = 1 . Como dissemos que n   >   0 , temos u = 1 .

Na quarta linha, entramos com a equação de diferenças na variável e q n , mas dando uma reformuladinha nela, jogando todos os termos para a esquerda e dizendo que ela é igual a 0 .

Passo 3

Com a equação de diferenças no MATLAB, podemos usar a função z t r a n s para calcular a transformada Z dela. Lembrando que z t r a n s tem como estrutura:

F = z t r a n s ( f )

Ela retorna a transformada Z da função f , armazenando-a na variável F . Quando não tem mais nenhuma entrada em z t r a n s além de f , o MATLAB assume que a variável independente de f é n e fará que a transformada Z F seja em função de z .

Acrescente em seu programa o comando abaixo para calcular a transformada Z de e q n :

O resultado é armazenado em E . Para ver como ficou E , rode o programa que fizemos até agora:

Ficou uma expressão bem comprida, mas dá pra perceber que tem um termo aí que aparece umas três vezes. z t r a n s ( y ( n ) ,   n ,   z ) tem exatamente a mesma estrutura da função z t r a n s e representa a transformada Z de y ( n ) , podendo ser substituído por Y ( z ) . No caso, chamaremos Y ( z ) só de Y .

Adicione os comandos abaixo em seu programa para fazer a substituição:

Primeiramente, criamos mais duas variáveis simbolicas: z e Y . Em seguida, usamos a função s u b s para pedir ao MATLAB que substitua em E a expressão z t r a n s ( y ( n ) ,   n ,   z ) por Y . O resultado da substituição é armazenado em E , ficando no lugar daquela expressão comprida que vimos.

Após a substituição, E fica assim:

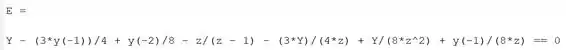
E tem mais coisa pra substituir aí. O enunciado disse para considerarmos as condições iniciais nulas, isto é, y - 1 = y - 2 = 0 . Para fazer as substituições, adicione ao seu programa a linha de código:

Com este comando, substituímos y ( - 1 ) por 0 e y ( - 2 ) por 0 em E e armazenamos a nova expressão em E , no lugar daquele E mostrado no print acima. Executando o programa, podemos ver como E está agora:

Passo 4

Para encontrar y ( n ) , precisamos encontrar Y ( z ) para daí aplicar nela i z t r a n s , para termos a inversa da tranformada Z. Em E , a variável Y representa Y ( z ) e podemos usar a função s o l v e do MATLAB para encontrá-la. Adicione em seu código:

Com este comando, a função s o l v e resolve a equação E para a variável Y e armazena a solução em Y , atualizando seu valor. Na prática, isolamos Y na equação com este comando e Y passa a representar a expressão algébrica de Y ( z ) . Rodando o programa, temos que Y é igual a:

Quer dizer que:

Y z = 8 z ³ 8 z 3 - 14 z 2 + 7 z - 1

Para encontrarmos y ( n ) , devemos aplicar a inversa da transformada Z em Y ( z ) , isto é, usar a função i z t r a n s do MATLAB em Y . A função i z t r a n s tem a estrutura:

f = i z t r a n s ( F )

Ela retorna a inversa da transformada Z de F , armazenando-a na variável f . Quando não tem mais nenhuma entrada em i z t r a n s além de F , o MATLAB assume que a variável independente de F é z e fará que a inversa da transformada Z f seja em função de n .

Para encontrar Y ( n ) , entre o comando:

Com este comando, o MATLAB calcula a inversa da transformada Z de Y e armazena o resultado em y , atualizando seu valor. y é a solução da equação de diferenças e, rodando o programa, é igual a:

Resposta

A resposta ao degrau unitário u n é:

y n = 1 4 n 3 - 2 1 2 n + 8 3

Exercício Resolvido #6

“Elaboração Própria”

Encontre a função de transferência H ( z ) e a resposta ao degrau unitário do sistema cuja equação das diferenças é dada por

y n = 1 2 y n - 1 + 2 x ( n )

Onde y ( n ) e x ( n ) são a saída e a entrada do sistema, respectivamente.

Passo 1

Uma função de transferência é a razão entre a saída e a entrada de um sistema. No tempo discreto, ela é obtida aplicando a transformada Z em uma equação das diferenças, considerando as condições iniciais nulas, e dividindo a saída pela entrada. Logo, H ( z ) será:

H z = Y ( z ) X ( z )

Onde Y ( z ) é a tranformada Z de y ( n ) e X ( z ) , de x ( n ) .

Para resolver o exercício, primeiramente aplicaremos a função z t r a n s do MATLAB na equação de diferenças para encontrarmos a transformada de y e x , que indicaremos por Y e X , respectivamente. Em seguida, manipularemos a equação para obtermos Y / X , que será a função de transferência H ( z ) .

Para obter a resposta ao degrau unitário do sistema, calcula-se produto entre H ( z ) e a transformada Z do degrau do unitário. Em seguida, usamos a função i z t r a n s para calcular sua transformada inversa, que será a solução do exercício.

Passo 2

Vamos rearranjar a equação, jogando todos os termos para a esquerda:

y n - 1 2 y n - 1 - 2 x n = 0

No MATLAB, vamos aplicar a função z t r a n s em cada termo da equação individualmente, pois dessa forma conseguiremos fazer a manipulação algébrica. Lembrando que z t r a n s tem a sintaxe:

F = z t r a n s ( f )

Ela retorna a transformada Z da função f , armazenando-a na variável F . Quando não tem mais nenhuma entrada em z t r a n s além de f , o MATLAB assume que a variável independente de f é n e fará que a transformada Z F seja em função de z .

A transformada Z dos termos da equação das diferenças será identificada assim:

t 1 = Z { y n }

t 2 = Z 1 2 y n - 1

t 3 = Z 2 x n

Onde Z { … } indica a transformada Z. Logo:

t 1 - t 2 - t 3 = 0

Considerando tudo isso, em um novo script, digite as linhas de código:

Na primeira linha, definimos as variáveis simbólicas n , x ( n ) e y ( n ) (indicamos que x e y são em função de n ).

Na segunda linha, assumimos que n   >   0 , para que o degrau unitário u , que será usado mais pra frente, seja igual a 1 .

Na terceira, quarta e quinta linha, a transformada Z de cada um dos termos da equação das diferenças rearranjada é calculada, sendo armazenada em t 1 , t 2 e t 3 .

Na sexta linha, montamos a transformada Z da equação das diferenças usando t 1 , t 2 e t 3 , fazendo-a igual a 0 . A transformada da equação é armazenada na variável E .

Vamos ver como ficou a equação após a aplicação da transformada Z? Execute o programa e imprima E no Command Window:

Passo 3

Podemos simplificar E : note que tem termos que tem exatamente a mesma estrutura da função z t r a n s e que representam transformadas que podem ser substituídas por uma única letra, indicando que é a transformada de uma função de n . z t r a n s ( y ( n ) ,   n ,   z ) representa a transformada Z de y ( n ) , podendo ser substituído por Y ( z ) . No caso, chamaremos Y ( z ) só de Y .

Já z t r a n s ( x ( n ) ,   n ,   z ) representa a transformada Z de x ( n ) , podendo ser substituído por X ( z ) . Como fizemos para Y ( z ) , chamaremos X ( z ) só de X .

Adicione os comandos abaixo em seu programa para fazer a substituição:

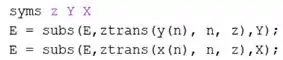
Primeiramente, criamos mais três variáveis simbolicas: z , Y e X . Em seguida, usamos a função s u b s para pedir ao MATLAB que substitua em E a expressão z t r a n s ( y ( n ) ,   n ,   z ) por Y . Logo abaixo, fazemos a mesma coisa para z t r a n s ( x ( n ) ,   n ,   z ) . O resultado da substituição é armazenado em E , ficando no lugar da expressão antiga.

E tem mais coisa que podemos substituir em E . Precisamos encontrar a função de transferência do sistema, que é determinada considerando as condições iniciais nulas. Logo, y - 1 = 0 . Para fazer a substiuição, adicione ao seu programa a linha de código:

Com este comando, substituímos y ( - 1 ) por 0 em E e armazenamos a nova expressão em E , atualizando a equação. Executando o programa, podemos ver como E está agora:

Bem mais bonitinho =)

Passo 4

Para calcular H ( z ) , precisamos dividir Y ( z ) por X ( z ) . Em E , a variável Y representa Y ( z ) e podemos usar a função s o l v e do MATLAB para isolá-la na equação. Adicione em seu código:

Com este comando, a função s o l v e resolve a equação E para a variável Y e armazena a solução em Y , atualizando seu valor. Na prática, isolamos Y na equação com este comando e Y passa a representar a expressão algébrica de Y ( z ) . Rodando o programa, temos que Y é igual a:

Para definir H ( z ) , basta dividir Y por X :

E temos que a função de transferência H é igual a:

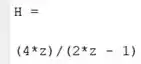
Passo 5

Com H , podemos calcular a resposta ao degrau unitário do sistema, que é dada pelo produto entre H ( z ) e a transformada Z do degrau do unitário. Para criar o degrau unitário, usaremos a função h e a v i s i d e , que tem a estrutura:

u = h e a v i s i d e ( n )

Ela cria um degrau unitário e o armazena em u : quando n   <   0 , u = 0 . Se n = 0 , u = 1 / 2 . Finalmente, para n >   0 , u = 1 . Como dissemos que n   >   0 , temos u = 1 .

Após criar o degrau com h e a v i s i d e , aplicamos z t r a n s nele para obter sua transformada Z.

Digite em seu programa os comandos:

Na primeira linha, criamos o degrau unitário e o armazenamos em u . Em seguida, calculamos sua transformada Z e a registramos em U .

Para encontrar a resposta ao degrau, inclua no seu programa o comando:

R é o produto entre H e U e representa a transformada Z da resposta ao degrau unitário.

Passo 6

Para finalizar, vamos calcular a transformada inversa de R para encontrar r ( n ) , a resposta do sistema ao degrau unitário no domínio de tempo discreto.

Para encontrarmos r ( n ) , vamos usar a função i z t r a n s do MATLAB em R . A função i z t r a n s tem a estrutura:

f = i z t r a n s ( F )

Ela retorna a inversa da transformada Z de F , armazenando-a na variável f . Quando não tem mais nenhuma entrada em i z t r a n s além de F , o MATLAB assume que a variável independente de F é z e fará que a inversa da transformada Z f seja em função de n .

Para encontrar r ( n ) , entre o comando:

Com este comando, o MATLAB calcula a inversa da transformada Z de R e armazena o resultado em r . Rodando o programa, r é igual a:

Resposta

A função de transferência H ( z ) é igual a:

H z = Y ( z ) X ( z ) = 4 z 2 z - 1

A resposta r ( n ) ao degrau unitário do sistema é:

r n = 4 - 2 1 2 n

Exercício Resolvido #7

“Adaptado de UNAL – Signal and Systems I (2016506) – Faculty of Engineering – Department of Electrical and Electronics Engineering. Tutorial 10 – Z-Transform, exercício 3”

Dado que x n = 3 n u [ n ] , onde u [ n ] é um degrau unitário, encontre a transformada Z de:

y n = n x n + x n - 1 u n - 1 + x n + 1 u [ n + 1 ]

Passo 1

O exercício pede para encontrarmos a transformada Z de y [ n ] , sabendo que x n = 3 n u [ n ] , sendo u [ n ] um degrau unitário.

Para isto, criaremos alguns degraus com a função h e a v i s i d e e aplicaremos a função z t r a n s do MATLAB na equação de diferenças para encontrarmos a transformada de y , que indicaremos por Y .

Passo 2

Sabemos que x n = 3 n u [ n ] e na equação de y [ n ] temos x [ n + 1 ] e x [ n - 1 ] . Logo, estes elementos podem ser substituídos por:

x n + 1 = 3 n + 1 u [ n + 1 ]

x n - 1 = 3 n - 1 u [ n - 1 ]

Por isso, vamos começar criando algumas funções degrau representando u [ n ] , u [ n + 1 ] e u [ n - 1 ] , para aplicarmos em seguida na equação de y [ n ] . Para criar as funções degraus, usaremos o comando h e a v i s i d e , que tem a estrutura:

u = h e a v i s i d e ( n )

Ela cria um degrau unitário e o armazena em u : quando n   <   0 , u = 0 . Se n = 0 , u = 1 / 2 . Finalmente, para n >   0 , u = 1 .

Em um novo script, digite as seguintes linhas de código:

Na primeira linha, definimos as variáveis simbólicas n e x ( n ) (indicamos que x é em função de n ).

Na segunda linha, assumimos que n   >   0 , para que o degrau unitário seja igual a 1 quando pertinente.

Na terceira linha, usamos a função h e a v i s i d e para criar o primeiro degrau unitário, que é armazenado em u _ n . Ele representa u [ n ] e será igual a 1 , pois assumimos que n > 0 .

Na quarta linha, criamos mais um degrau unitário usando h e a v i s i d e , para representar u [ n + 1 ] . Ele é armazenado em u _ n _ m a i s _ 1 e também é igual a 1 , pois n > 0 .

Na quinta linha, criamos o terceiro degrau unitário usando h e a v i s i d e , representando u [ n - 1 ] . Ele é armazenado em u _ n _ m e n o s _ 1 , e não terá um valor definido como os outros acima, pois ele pode ser igual a 0 , 1 / 2 ou 1 , dependendo do valor de n .

Passo 3

Após criar u _ n , u _ n _ m a i s _ 1 e u _ n _ m e n o s _ 1 , entre com a equação de y [ n ] , sem substituir x [ n ] por enquanto:

A equação que define y [ n ] é armazenada na variável y . Vamos ver como ficou? Execute o programa e imprima y no Command Window:

Repare que o u _ n e u _ n _ m a i s _ 1 não estão mais ali, por serem iguais a 1 . O u _ n _ m e n o s _ 1 foi substituído por h e a v i s i d e ( n - 1 ) , por não ter um valor definido.

Vamos agora fazer as substituições de x [ n ] por 3 n u [ n ] , de x [ n - 1 ] por 3 n - 1 u [ n - 1 ] e de x [ n + 1 ] por 3 n + 1 u [ n + 1 ] , usando o comando s u b s :

Com o comando acima, eu peço ao MATLAB para substituir, em y , x ( n ) por 3 ^ n * u _ n , x ( n - 1 ) por 3 ^ ( n - 1 ) * u _ n _ m e n o s _ 1 e x ( n + 1 ) por 3 ^ ( n + 1 ) * u _ n _ m a i s _ 1 . O resultado da substituição é armazenado em y , ficando no lugar da expressão que vimos no print mais acima.

Ah, e repare que eu usei o . . . para quebrar a linha de comando no MATLAB. É um jeito de a linha caber na sua tela sem ter que usar uma barra de rolagem horizontal para ver o código todo.

Vamos ver a nova cara de y :

Passo 4

Após fazer as substituições, vamos finalmente calcular a transformada Z de y [ n ] . Para isto, usaremos a função z t r a n s , que tem a sintaxe:

F = z t r a n s ( f )

Ela retorna a transformada Z da função f , armazenando-a na variável F . Quando não tem mais nenhuma entrada em z t r a n s além de f , o MATLAB assume que a variável independente de f é n e fará que a transformada Z F seja em função de z .

Inclua no seu programa os comandos:

O primeiro comando calcula a transformada Z de y e a armazena na variável Y .

O segundo comando simplifica a expressão de Y , pondo em evidência alguns termos e cortando o que dá cortar. Desta forma, o resultado fica mais enxuto.

Execute o programa e veja a transformada Z de y imprimindo Y no Command Window:

Resposta

Z y n = Y z = z ( 10 z - 21 ) 3 z - 3 2

Exercício Resolvido #8

“Adaptado de UNAL – Signal and Systems I (2016506) – Faculty of Engineering – Department of Electrical and Electronics Engineering. Tutorial 10 – Z-Transform, exercício 7”

Um sistema LIT de tempo discreto é descrito por

y n + 2 + 1 2 y n + 1 + y n = x n + 1 + 2 x [ n ]

  1. Obtenha a função de transferência do sistema, tendo y [ n ] como saída e x [ n ] como entrada;
  2. Obtenha a resposta do sistema a um degrau unitário.

Passo 1

Uma função de transferência é a razão entre a saída e a entrada de um sistema. No tempo discreto, ela é obtida aplicando a transformada Z em uma equação das diferenças, considerando as condições iniciais nulas, e dividindo a saída pela entrada. Logo, a função de transferência H [ z ] será:

H [ z ] = Y [ z ] X [ z ]

Onde Y [ z ] é a tranformada Z de y [ n ] e X [ z ] , de x [ n ] .

Para resolver a letra a o exercício, primeiramente aplicaremos a função z t r a n s do MATLAB na equação de diferenças para encontrarmos a transformada de y e x , que indicaremos por Y e X , respectivamente. Em seguida, manipularemos a equação para obtermos Y / X , que será a função de transferência H [ z ] .

Para resolver a letra b do exercício, calcula-se produto entre H [ z ] e a transformada Z do degrau do unitário, que é criado usando a função h e a v i s i d e . Em seguida, usamos a função i z t r a n s para calcular sua transformada inversa e encontrar a resposta ao degrau.

Passo 2

Para resolver a letra a, vamos rearranjar a equação, jogando todos os termos para a esquerda:

y n + 2 + 1 2 y n + 1 + y n - x n + 1 - 2 x n = 0

No MATLAB, vamos aplicar a função z t r a n s em cada termo da equação individualmente, pois dessa forma conseguiremos fazer a manipulação algébrica que nos dará a função de transferência. Lembrando que z t r a n s tem a sintaxe:

F = z t r a n s ( f )

Ela retorna a transformada Z da função f , armazenando-a na variável F .

A transformada Z dos termos da equação das diferenças será identificada da seguinte maneira:

t 1 = Z { y n + 2 }

t 2 = Z 1 2 y n + 1

t 3 = Z y n

t 4 = Z x n + 1

t 5 = Z 2 x n

Onde Z { … } indica a transformada Z. Logo:

t 1 + t 2 + t 3 - t 4 - t 5 = 0

Considerando tudo isso, em um novo script, digite as linhas de código:

Na primeira linha, definimos as variáveis simbólicas n , x ( n ) e y ( n ) (indicamos que x e y são em função de n ).

Na segunda linha, assumimos que n   >   0 , para que o degrau unitário u , que será usado para resolver a letra b, seja igual a 1 .

Na terceira, quarta, quinta, sexta e sétima linha, a transformada Z de cada um dos termos da equação das diferenças rearranjada é calculada, sendo armazenada em t 1 , t 2 , t 3 , t 4 e t 5 .

Após definir os termos da equação, construa a transformada Z dela a partir de t 1 , t 2 , t 3 , t 4 e t 5 , com o comando:

Desta forma, a transformada da equação é armazenada na variável E .

Vamos ver como ficou a equação após a aplicação da transformada Z, executando o programa e imprimindo E no Command Window:

Passo 3

Nossa, E tá enorme, nem dá pra ler. Mas podemos deixar E mais enxuto: ele tem termos que têm exatamente a mesma estrutura da função z t r a n s e que representam transformadas que podem ser substituídas por uma única letra, indicando que é a transformada de uma função de n . z t r a n s ( y ( n ) ,   n ,   z ) representa a transformada Z de y ( n ) , podendo ser substituído por Y ( z ) . No caso, chamaremos Y ( z ) só de Y .

Já z t r a n s ( x ( n ) ,   n ,   z ) representa a transformada Z de x ( n ) , podendo ser substituído por X ( z ) . Como fizemos para Y ( z ) , chamaremos X ( z ) só de X .

Adicione os comandos abaixo em seu programa para fazer a substituição:

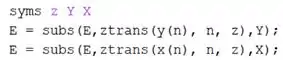
Primeiramente, criamos mais três variáveis simbolicas: z , Y e X . Em seguida, usamos a função s u b s para pedir ao MATLAB que substitua em E a expressão z t r a n s ( y ( n ) ,   n ,   z ) por Y . Logo abaixo, fazemos a mesma coisa para z t r a n s ( x ( n ) ,   n ,   z ) . O resultado da substituição é armazenado em E , ficando no lugar da expressão antiga:

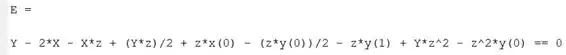
Nossa, bem melhor. E tem mais coisa que podemos substituir em E . Precisamos encontrar a função de transferência do sistema, que é determinada considerando as condições iniciais nulas. Logo, x 0 = y 0 = y ( 1 ) = 0 . Para fazer a substiuição, adicione ao seu programa a linha de código:

Com este comando, substituímos x 0 ,   y ( 0 ) e y ( 1 ) por 0 em E e armazenamos a nova expressão em E , atualizando a equação. Executando o programa, podemos ver como E está agora:

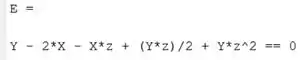
Bem mais agradável de se olhar!

Passo 4

Para calcular H [ z ] , precisamos dividir Y [ z ] por X [ z ] . Em E , a variável Y representa Y [ z ] e podemos usar a função s o l v e do MATLAB para isolá-la na equação. Adicione em seu código:

Com este comando, a função s o l v e resolve a equação E para a variável Y e armazena a solução em Y , atualizando seu valor. Na prática, isolamos Y na equação com este comando e Y passa a representar a expressão algébrica de Y [ z ] . Rodando o programa, temos que Y é igual a:

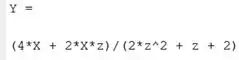
Para definir H [ z ] , divida Y por X , já aplicando a função s i m p l i f y para eliminar o X do numerador de Y :

E temos que a função de transferência H é igual a:

Está aí a resposta da letra a ;)

Passo 5

Com H , podemos resolver a letra b do exercício e calcular a resposta ao degrau unitário do sistema, que é dada pelo produto entre H [ z ] e a transformada Z do degrau do unitário. Para criar o degrau unitário, usaremos a função h e a v i s i d e , que tem a estrutura:

u = h e a v i s i d e ( n )

Ela cria um degrau unitário e o armazena em u : quando n   <   0 , u = 0 . Se n = 0 , u = 1 / 2 . Finalmente, para n >   0 , u = 1 . Como dissemos que n   >   0 , temos u = 1 .

Após criar o degrau com h e a v i s i d e , aplicamos z t r a n s nele para obter sua transformada Z. Por isso, digite em seu programa os comandos:

Na primeira linha, criamos o degrau unitário e o armazenamos em u . Em seguida, calculamos sua transformada Z e a registramos em U .

Para encontrar a resposta ao degrau, inclua no seu programa o comando:

R é o produto entre H e U e representa a transformada Z da resposta ao degrau unitário:

Passo 6

Para finalizar, vamos calcular a transformada inversa de R para encontrar r [ n ] , a resposta do sistema ao degrau unitário no domínio de tempo discreto.

Para encontrarmos r [ n ] , vamos aplicar a função i z t r a n s do MATLAB em R . A função i z t r a n s tem a estrutura:

f = i z t r a n s ( F )

Ela retorna a inversa da transformada Z de F , armazenando-a na variável f .

Para encontrar r [ n ] , digite os comandos:

Com o primeiro comando, o MATLAB calcula a inversa da transformada Z de R e armazena o resultado em r . O segundo comndo simplifica r , para deixá-lo mais enxuto.

Rodando o programa, r é igual a:

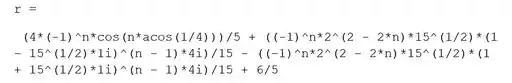
Resposta

  1. A função de transferência é:

    2. H z = 2 z + 4 2 z 2 + z + 2

  2. A resposta ao degrau unitário é:

r n = 4 - 1 n cos ⁡ n cos - 1 ⁡ 1 / 4 5 + - 1 n 2 2 - 2 n 15 1 - 15 i n - 1 4 i 1 5 - - 1 n 2 2 - 2 n 15 1 + 15 i n - 1 4 i 15 + 6 5