Sistemas de Equações Lineares
Produzido por Gustavo BarbosaTeoria
Introdução
Fala, galera mais linda do Brasil! Espero que estejam animados porque hoje vamos aprender bastaaaante coisa!
Lembram das aulas de Álgebra Linear, em que aprendemos como resolver sistemas de equações lineares?
É um conteúdo que aprendemos no início da graduação e que depois usamos muito em disciplinas mais aplicadas das engenharias, como Mecânica dos Sólidos e Circuitos Elétricos. Por isso, é muito importante ter ferramentas computacionais na mão quando aparecerem exercícios de disciplinas ou até mesmo em projetos de Engenharia.
“Putz, mas nem lembro mais como se resolvem sistemas de equações! Tô ferrado pelo resto da minha graduação?”, você deve estar pensando. “Oh, e agora? Quem poderá me ajudar?”

Palma, palma! Não priemos cânico! Eu posso te ajudar! =D
Hoje vamos ver como resolvemos sistemas de equações lineares no MATLAB. Você vai ver que com algumas linhas de código conseguimos encontrar rapidinho a solução de sistemas enooormes!
Resolvendo sistemas de equações lineares
Digamos que você queira resolver o seguinte sistema de equações lineares:
Temos três equações e três incógnitas: , e .
Existem várias formas de resolver um sistema de equações lineares no MATLAB. Mas para poder entrar com o sistema de equações no MATLAB, antes devemos deixá-lo no formato matricial:
Onde é uma matriz com os coeficientes das equações, é o vetor com as incógnitas e é o vetor com os valores numéricos à direita do sinal de igual, que não são multiplicados por nenhuma incógnita.
Para o sistema de equações lineares do nosso circuito, temos:
A matriz e os vetores do sistema de equações no formato matricial são as entradas das formas do MATLAB de resolver sistemas de equações lineares. Vamos conhecer estas formas aplicando-as diretamente no nosso exemplo.
Vamos construir em um script novo do MATLAB a matriz de coeficientes do nosso sistema de equações e o vetor :
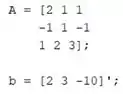
Para construir o vetor , primeiro eu criei um vetor linha e com a aspas simples () eu o transpus e o tranformei em vetor coluna, para ficar igual ao vetor mostrado na parte que construímos a forma matricial do sistema de equações.
Reparou que só entramos com e ? É porque o vetor será a solução do sistema de equações e será o MATLAB quem vai nos dar.
Agora vamos ver as formas com as quais o MATLAB pode resolver nosso sistema.
Forma 1: inversa da matriz A
Vamos dar uma manipulada na forma matricial do sistema de equações , pré-multiplicando cada lado da equação pela inversa de :
Lembra que quando multiplicamos uma matriz pela sua inversa obtemos a matriz identidade ? E quando multiplicamos uma matriz ou um vetor por , o resultado é a própria matriz ou o próprio vetor? Usando essas propriedades na equação acima, temos:
Isto quer dizer que, para encontrarmos a solução do sistema linear de equações, representada pelo vetor , podemos simplesmente pré-multiplicar o vetor pela inversa da matriz de coeficientes . No MATLAB, para o nosso exemplo, a solução do sistema de equações se dá pela seguinte linha de código:
![]()
A função calcula a inversa de uma matriz quadrada.
Ao rodarmos o programa, encontramos que é igual a:

O vetor calculado pelo MATLAB é a solução do sistema de equações lineares. Isto quer dizer que , e .
Apesar de bem prática, esta não é a melhor forma de resolver um sistema de equações. O próprio MATLAB não recomenda usá-la, pois ele tem recursos mais precisos para encontrar a solução. Para um sistema pequenininho de equações, isso pode não fazer diferença, mas se você estiver trabalhando com sistemas maiores, tipo os que vemos em Resistência dos Materiais, é bom termos a melhor precisão possível.
Além disso, pode acontecer de você ter um sistema de equações indeterminado: um sistema onde há mais incógnitas do que equações. Sistemas assim têm infinitas soluções, ao contrário do sistema do nosso exemplo, que é determinado (o número de equações é igual ao número de incógnitas) e possui solução única.
A matriz de um sistema indeterminado não é quadrada, logo, não tem inversa. Por isso é bom conhecer as outras formas que o MATLAB tem para resolver sistemas de equações lineares.
Forma 2: divisão de matrizes
A segunda forma que veremos para resolver o sistema de equações é usando o que se chama de “divisão de matrizes”, usando o símbolo \ (barra invertida).
No MATLAB, substitua o comando por:
![]()
Quando usamos a barra invertida, a matriz de coeficientes (no nosso caso, a matriz ) sempre deve vir antes da barra , como na linha de código acima. Em seguida, vem o vetor com os valores numéricos à direita da igualdade, independentes das incognitas (no nosso caso, o vetor ). Para a barra invertida funcionar, e devem ter o mesmo número de linhas.
Ao rodarmos o programa, obtemos a seguinte solução:
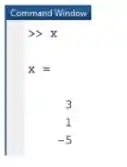
Note que é exatamente o mesmo resultado obtido através de .
Além da maior precisão, outra vantagem de usar a barra invertida é que ela nos retorna uma solução mesmo se o sistema for indeterminado (matriz retangular). Mas não se esqueça que, neste caso, a solução é apenas uma de infinitas possibilidades.
Forma 3: linsolve
Outra forma de resolver sistemas de equações lineares no MATLAB é usando a função . Ela tem a estrutura:
As entradas da função são a matriz de coeficientes e o vetor contendo os valores à direita da igualdade, o vetor . A matriz e o vetor devem ter o mesmo número de linhas para funcionar.
A saída da função é o vetor , que contém a solução do sistema de equações.
No script do nosso exemplo, substitua por:
![]()
Rodando nosso programa, vemos que o resultado é o mesmo obtido usando as formas 1 e 2:
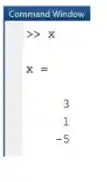
A função também dá uma das infinitas soluções de um sistema indeterminado, isto é quando a matriz é retangular.
Outra característica de , que não veremos em detalhes aqui mas é bom saber que existe, é que ela tem uma entrada opcional onde podemos informar a estrutura da matriz (por exemplo, se ela é triangular). Desta forma, o MATLAB consegue escolher a maneira mais eficiente de resolver o sistema. Isto pode ajudar a resolver sistemas com muuuuuuitas equações de uma maneira mais rápida.
Forma 4: rref
Para finalizar, vamos conhecer a função , que pode ajudar a resolver sistemas determinados e a encontrar soluções para sistemas indeterminados.
A função escalona uma matriz. O nome da função vem do inglês “reduced row echelon form”, que em português quer dizer “forma escalonada reduzida”.
Com um exemplo, fica mais fácil de entender. Digamos que temos a matriz:
Ao aplicarmos a função nela no MATLAB, ele vai nos retornar:
Vamos listar as características da matriz que a função retornou:
- As linhas da matriz que só têm zeros são as últimas da matriz;
- O primeiro elemento diferente de de uma linha está em uma coluna à direita do elemento não nulo da linha de cima;
- Os primeiros elementos diferentes de das linhas são iguais a e são os únicos elementos diferentes de nas suas colunas.
Essas são as características de uma matriz escalonada reduzida.
Agora que conhecemos o básico do que é uma matriz escalonada reduzida e como fazer uma no MATLAB, vamos voltar ao nosso exemplo do circuito elétrico para ver como podemos usar o para resolver um sistema de equações lineares.
A primeira coisa a fazer é criar uma matriz aumentada com e , entrando o seguinte comando no MATLAB:
![]()
Este comando cria uma nova matriz , que será uma matriz , sendo ela uma concatenação da matriz com o vetor . Em outras palavras, este comando vai adicionar uma coluna à matriz , correspondendo ao vetor . Para compreender melhor, a matriz será igual a:
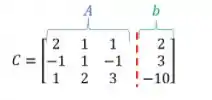
Para encontrar a solução do sistema linear de equações com a matriz aumentada , aplicamos nela a função , usando o comando:
![]()
Neste comando, cria-se a matriz escalonada reduzida da matriz aumentada usando a função . A saída de é a matriz escalonada reduzida de e é armazenada na variável .
A solução do sistema de equações está na matriz . Vamos pedir ao MATLAB para imprimi-la no Command Window:

Perceba que as três primeiras colunas de compõem uma matriz identidade . Isto quer dizer que nosso sistema de equações, com equações e incógnitas, tem solução única. Esta solução única está na quarta coluna de .
Podemos colocar no formato de equações novamente e temos:
Concluindo
Vamos fazer um balanço das quatro formas de resolver sistemas de equações lineares que vimos aqui:
- A inversão de matriz () não é a mais recomendada, pois tem baixa precisão e não fornece uma solução caso tenhamos mais incógnitas do que equações;
- A resolução por divisão de matrizes (uso da barra invertida, ) tem maior precisão e fornece uma das posssíveis soluções de um sistema com mais incógnitas do que equações;
- O comando permite informar ao MATLAB a estrutura da matriz , para que ele aplique um método de resolução que seja mais eficiente para essa estrutura. Isso é muito bom caso tenhamos um código onde temos que resolver vários sistemas lineares ou para sistemas muuuuito grandes, pois diminui o custo computacional;
- Finalmente, o comando é recomendado caso você queira fazer alguma análise de álgebra linear do sistema de equações.
Ufa! Vimos bastante coisa hoje, né? Agora, bora praticar ;D
Forma 1: inversa da matriz A
Forma 2: divisão de matrizes
Forma 3: linsolve
Forma 4: rref
Concluindo
Exercícios Resolvidos
Exercício Resolvido #1
“UnB - Laboratorio de Análise Dinâmica Linear – Simulação de Distemas Dinâmicos. Exercícios para o relatório – Exercício 1 (2017)”
Escreva um algoritmo em arquivo ‘.m’ para resolver o seguinte sistema de equações lineares:
Passo 1
O exercício nos dá um um sistema de equações lineares, com três equações e três incógnitas. As incógnitas são , e .
O enunciado pede para solucionarmos o sistema linear, isto é, encontrarmos os valores de , e . Para isto, usaremos uma das funções que vimos para resolver sistemas de equações lineares no MATLAB: matriz inversa, barra invertida, ou o .
Passo 2
Primeiramente, vamos passar o sistema de equações lineares para o formato matricial:
Onde é uma matriz com os coeficientes das equações, é o vetor com as incógnitas , e e é o vetor com os valores numéricos à direita do sinal de igual, que não são multiplicados por nenhuma incógnita.
No formato matricial, temos:
Crie um script novo no MATLAB e entre a matriz e o vetor :
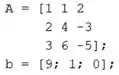
Passo 3
Após entrar com e , podemos resolver o sistema de equações e encontrar o vetor , representando a solução do sistema.
Vimos quatro formas de resolver um sistema linear no MATLAB: inversão de matriz , barra invertida, e . Para resolver este exercício, recomendo utilizar qualquer uma das três primeiras opções, menos a , pois vamos praticar seu uso em outros exercícios mais pra frente. Mas caso queira usar a , não esqueça de construir a matriz aumentada .
Forma 1: inversa da matriz
Caso queira usar a inversão da matriz para resolver o sistema, digite no script a linha de código:
![]()
Forma 2: barra invertida (divisão de matrizes)
Caso queira usar a barra invertida para resolver o sistema, digite a linha de código:
![]()
Forma 3:
Caso queira usar a função para resolver o sistema, digite a linha de código:
![]()
Qualquer uma das três formas retornará o mesmo vetor . Rode seu programa e ele calculará o vetor como:
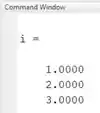
Isto significa que a solução do sistema de equações lineares é , e .
Resposta
A solução do sistema de equações lineares é
Exercício Resolvido #2
“UFC – Apostila de MATLAB – PET Engenharia Elétrica. Exercício 2, p. 14 (2014)”
Resolva o seguinte sistema de equações lineares:

Passo 1
O exercício nos dá um um sistema de equações lineares, com três equações e três incógnitas. As incógnitas são , e .
O enunciado pede para solucionarmos o sistema linear, isto é, encontrarmos os valores de , e . Para isto, usaremos uma das funções que vimos para resolver sistemas de equações lineares no MATLAB: matriz inversa, barra invertida, ou o .
Passo 2
Primeiramente, vamos passar o sistema de equações lineares para o formato matricial:
Onde é uma matriz com os coeficientes das equações, é o vetor com as incógnitas , e e é o vetor com os valores numéricos à direita do sinal de igual, que não são multiplicados por nenhuma incógnita.
No formato matricial, temos:
Note que a terceira equação, , não tem a incógnita , por isso o primeiro elemento da terceira linha de é .
Agora, crie um script novo no MATLAB e entre com a matriz e o vetor :

Passo 3
Após entrar com e , podemos resolver o sistema de equações e encontrar o vetor , representando a solução do sistema.
Vimos quatro formas de resolver um sistema linear no MATLAB: inversão de matriz , barra invertida, e . Para resolver este exercício, recomendo utilizar qualquer uma das três primeiras opções, menos a , pois vamos praticar seu uso em outros exercícios mais pra frente. Mas caso queira usar a , não esqueça de construir a matriz aumentada .
Forma 1: inversa da matriz
Caso queira usar a inversão da matriz para resolver o sistema, digite no script a linha de código:
![]()
Forma 2: barra invertida (divisão de matrizes)
Caso queira usar a barra invertida para resolver o sistema, digite a linha de código:
![]()
Forma 3:
Caso queira usar a função para resolver o sistema, digite a linha de código:
![]()
Qualquer uma das três formas retornará o mesmo vetor . Rode seu programa e ele calculará o vetor como:

Isto significa que a solução do sistema de equações lineares é , e .
Resposta
A solução do sistema linear de equações é:
Exercício Resolvido #3
“Adaptado de MATLAB® for Engineering Applications, de William J. Palm III, McGraw-Hill Education, 4ª edição, 2019. Exemplo 8.2-2, p. 327”
A figura abaixo mostra uma massa suspensa por três cabos presos em três pontos B, C e D.
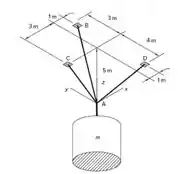
As tensões nos cabos AB, AC e AD são representadas por , e , respectivamente. Se a massa está em equilíbrio estático, a soma dos componentes das tensões nas direções , e deve ser igual a . Isso resulta nas seguintes três equações:
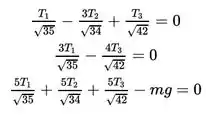
Determine , e . Considere e .
Passo 1
O exercício nos dá um um sistema de equações lineares, com três equações e três incógnitas. As incógnitas são , e .
O enunciado pede para solucionarmos o sistema linear, isto é, encontrarmos os valores de , e . Para isto, usaremos uma das funções que vimos para resolver sistemas de equações lineares no MATLAB: matriz inversa, barra invertida, ou o .
Passo 2
Primeiramente, vamos passar o sistema de equações lineares para o formato matricial:
Onde é uma matriz com os coeficientes das equações, é o vetor com as incógnitas , e e é o vetor com os valores numéricos à direita do sinal de igual, que não são multiplicados por nenhuma incógnita.
Para colocarmos o sistema no formato matricial, temos que dar uma manipuladinha na terceira equação do sistema, jogando à direita da igualdade:
Logo, este é o nosso sistema de equações:
No formato matricial, temos:
Agora, crie um script novo no MATLAB, entre com a massa , a aceleração da gravidade , a matriz e o vetor :

Passo 3
Após entrar com e , podemos resolver o sistema de equações e encontrar o vetor , representando a solução do sistema.
Vimos quatro formas de resolver um sistema linear no MATLAB: inversão de matriz , barra invertida, e . Para resolver este exercício, recomendo utilizar qualquer uma das três primeiras opções, menos a , pois vamos praticar seu uso em outros exercícios mais pra frente. Mas caso queira usar a , não esqueça de construir a matriz aumentada .
Forma 1: inversa da matriz
Caso queira usar a inversão da matriz para resolver o sistema, digite no script a linha de código:
![]()
Forma 2: barra invertida (divisão de matrizes)
Caso queira usar a barra invertida para resolver o sistema, digite a linha de código:
![]()
Forma 3:
Caso queira usar a função para resolver o sistema, digite a linha de código:
![]()
Qualquer uma das três formas retornará o mesmo vetor . Rode seu programa e ele calculará o vetor como:
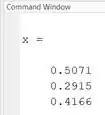
Isto significa que a solução do sistema de equações lineares é , e .
Resposta
As tensões nos cabos AB, AC e AD são , e , respectivamente
Exercício Resolvido #4
“Adaptado de UERJ, Curso de MATLAB 5.1: Introdução à Solução de Problemas de Engenharia, Laboratório de Engenharia Elétrica, p. 104”
Considere o sistema de equações lineares abaixo:
- Resolva o sistema de equações lineares usando o MATLAB;
- Plote as retas das equações e indique no gráfico a solução encontrada na letra a.
Passo 1
O exercício é dividido em duas partes: na letra a, ele nos pede para resolver um sistema de equações lineares composto por duas equações e duas incógnitas. Para isso, podemos usar qualquer um dos comandos aprendidos na aula: matriz inversa, barra invertida, ou o .
Na letra b, o exercício pede para plotarmos as retas das equações e indicar no gráfico gerado o ponto que representa a solução encontrada na letra a. É possível fazer isso porque podemos manipular as equações do sistema para um formato ou (dá na mesma usar qualquer um dos formatos) e plotar as retas em um plano. O ponto onde as duas retas representanto as equações se encontram, isto é, o ponto de intersecção das duas retas, representa a solução do sistema de equações lineares obtida na letra a.
Passo 2
Vamos começar respondendo a letra a. Primeiramente, vamos passar o sistema de equações lineares para o formato matricial:
Onde é uma matriz com os coeficientes das equações, é o vetor com as incógnitas e e é o vetor com os valores numéricos à direita do sinal de igual, que não são multiplicados por nenhuma incógnita.
Para o sistema:
Temos:
Agora, crie um script novo no MATLAB e digite a matriz e o vetor :

Eu entrei o vetor como um vetor linha e transpus ele, usando a aspas simples (), para ele se tornar um vetor coluna. Mas você pode entrar com da forma que quiser.
Passo 3
Após entrar com e , podemos resolver o sistema de equações e encontrar o vetor , representando a solução do sistema.
Vimos quatro formas de resolver um sistema linear no MATLAB: inversão de matriz , barra invertida, e . Para resolver este exercício, recomendo utilizar qualquer uma das três primeiras opções, menos a , pois vamos praticar seu uso em outros exercícios mais pra frente. Mas caso queira usar a , não esqueça de construir a matriz aumentada .
Forma 1: inversa da matriz
Caso queira usar a inversão da matriz para resolver o sistema, digite no script a linha de código:
![]()
Forma 2: barra invertida (divisão de matrizes)
Caso queira usar a barra invertida para resolver o sistema, digite a linha de código:
![]()
Forma 3:
Caso queira usar a função para resolver o sistema, digite a linha de código:
![]()
Qualquer uma das três formas retornará o mesmo vetor . Rode seu programa e ele calculará o vetor como:

Isto quer dizer que a solução do sistema de equações lineares é e . Esta é a resposta da letra a do exercício.
Passo 4
Vamos responder à letra b, que nos pede para gerar um gráfico com as equações do sistema e, em seguida, indicar no gráfico a solução do sistema obtida na letra a.
A primeira coisa que devemos fazer é dar uma manipulada nas equações, para deixá-las na forma ou . Eu escolhi o formato , mas se quiser o formato , sem problemas, o resultado será o mesmo.
Deixando as equações no formato , temos:
Você pode usar o mesmo script do MATLAB onde você fez a letra a ou criar um novo, tanto faz. Para podermos gerar o gráfico, vamos criar um vetor z indo de a , com um passo igual a , com o comando:
![]()
Em seguida, vamos calcular dois vetores, e , representando as funções acima:
![]()
representa o resultado da função , para cada elemento do vetor . Da mesma forma, representa a função , calculada para cada elemento de .
Passo 5
Após criarmos os vetores e , podemos plotar as retas representando as equações do sistema linear. Para isto, digite os comandos:
![]()
O primeiro comando gera, em um mesmo gráfico, as retas representando e .
O primeiro par dentro do , , representa e indica que está no eixo horizontal do gráfico e que está no eixo vertical do gráfico.
Da mesma forma, o segundo par indica que está no eixo horizontal e que está no eixo vertical e representa .
O segundo comando pede que o gráfico gerado pelo tenha linhas de grade, para facilitar a identificação das coordenadas dos pontos das retas.
Ao rodarmos o programa, temos este gráfico:
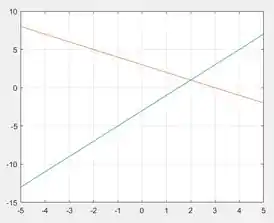
A reta azul representa e a reta vermelha, .
Para indicar no gráfico a solução da letra a, clique no ponto onde as retas se encontram. Veja pelas linhas de garde que elas se interceptam bem em . O MATLAB mostrará as coordenadas do ponto onde você clicou. As coordenadas do ponto de intersecção das retas são a solução do sistema de equações lineares do exercício.
Resposta
- A solução do sistema de equações lineares é e .
- O gráfico abaixo apresenta as retas representando as equações do sistema:

As coordenadas do ponto de intersecção, apresentado no gráfico, representam a solução encontrada na letra a.
Exercício Resolvido #5
“UNICAMP - Lista de exercícios sobre sistemas lineares de INF903 - INTRODUÇÃO AO MATLAB (2003). Exercício 1”
Considere o sistema linear:
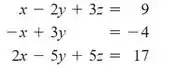
- Use o comando do MATLAB para resolver o sistema;
- Seja a matriz de coeficientes do sistema, e o lado direito das equações:

Use o comando do MATLAB para resolver o sistema.
Passo 1
O exercício nos dá um sistema de equações lineares de 3 equações com 3 incógnitas. Na letra a, ele nos pede para resolver o sistema usando a função , que dá a forma escalonada reduzida de uma matriz.
Para resolver um sistema de equações lineares usando , temos que passar o sistema para o formato matricial:
Onde é uma matriz com os coeficientes das equações, é o vetor com as incógnitas (no caso, , e ) e é o vetor com os valores numéricos à direita do sinal de igual, que não são multiplicados por nenhuma incógnita.
Com a matriz de coeficientes e o vetor , construímos a matriz aumentada . É a matriz aumentada que vai ser escalonada com o , e é a partir da análise de sua forma escalonada reduzida que encontramos uma solução para o sistem linear de equações.
A letra b nos dá a matriz de coeficientes A e o vetor B e pede para resolvermos o mesmo sistema de equações lineares de outra forma: usando a divisão de matrizes, ou seja, a barra invertida ().
Este exercício é legal porque podemos praticar duas formas diferentes de resolver o sistema e comparar os resultados.
Passo 2
Vamos resolver a letra a. A primeira coisa a fazer é criar um script novo no MATLAB e entrar com a matriz de coeficientes e o vetor , que nos são dados na letra b do exercício:
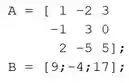
Em seguida, vamos construir a matriz aumentada , usando a linha de código:
![]()
Este comando cria uma nova matriz que é uma junção da matriz com o vetor . Basicamente, adicionamos mais uma coluna à , correspondendo a . Fica melhor de visualizar se pedirmos ao MATLAB para imprimir a matriz aumentada :

Repare que as três primeiras colunas de são a matriz e a última coluna, o vetor .
Passo 3
É com a matriz aumentada que encontraremos a solução do sistema linear, usando-a como entrada da função . No seu script do MATLAB, adicione a linha de código:
![]()
Esta linha de código cria a forma escalonada reduzida de , por meio do , e a armazena na variável .
A solução do sistema de equações está na matriz . Rode seu programa e peça ao MATLAB para imprimi-la no Command Window:

Perceba que as três primeiras colunas de compõem uma matriz identidade . Isto quer dizer que nosso sistema de equações, com equações e incógnitas, tem solução única. Esta solução única está na quarta coluna de .
Podemos voltar ao formato de sistema de equações partindo de . Este processo nos dará a solução do sistema linear, pois teremos:
Pronto! Esta é a solução do sistema. Letra a respondida ;D
Passo 4
Vamos responder à letra b do exercício. Ela pede para resolvermos o mesmo sistema de equações, mas usando divisão de matrizes.
Vamos resolver a letra b no mesmo script onde fizemos a letra a. Como já entramos com a matriz de coeficientes e o vetor , basta adicionarmos a seguinte linha de código para respondermos a letra b:
![]()
O comando calculará a solução do sistema de equações e armazenará o resultado no vetor .
Vamos rodar o programa e pedir ao MATLAB para nos mostrar :
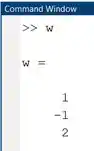
Repare que é igualzinho à quarta coluna de . Logo, chegamos ao mesmo resultado usando e .
Resposta
- A solução do sistema, usando , é:
- A solução do sistema linear de equações, usando , é:
Exercício Resolvido #6
“UNICAMP - Lista de exercícios sobre sistemas lineares de INF903 - INTRODUÇÃO AO MATLAB (2003). Exercício 2”
Entre a matriz no MATLAB:
Use o comando do MATLAB para encontrar a forma escalonada reduzida de . Qual é a solução do sistema linear representado pela matriz aumentada ?
Passo 1
Este exercício nos dá uma matriz e pede para aplicarmos a função nela, para encontrarmos a sua forma escalonada reduzida.
Em seguida, o exercício pergunta qual é a solução do sistema linear representado pela matriz aumentada .
Mas neste exercício não vai ser fácil encontrar uma solução para o sistema linear. Lembra que uma matriz aumentada é a adição de uma coluna a mais na matriz de coeficientes do sistema linear? Em outras palavras, se o nosso sistema linear está no formato matricial:
Onde é uma matriz com os coeficientes das equações, é o vetor com as incógnitas e é o vetor com os valores numéricos à direita do sinal de igual, que não são multiplicados por nenhuma incógnita.
A matriz aumentada é igual a . No caso da matriz do enunciado, temos que:
Perceba que é uma matriz retangular, com 3 linhas e 4 colunas. Isto quer dizer que ela é matriz de coeficientes de um sistema com 3 equações e 4 incógnitas, logo, se trata de um sistema indeterminado, com infinitas soluções.
Portanto, neste exercício, não teremos uma solução única, mas sim, algumas equações que serão obtidas da saída de que representam as infinitas soluções do sistema linear.
Com o passo a passo, vai ficar mais fácil de entender.
Passo 2
Crie um script novo no MATLAB, entre com a matriz e calcule sua forma escalonada reduzida usando a função :

A forma escalonada reduzida de é armazenada na variável . Ao rodarmos o programa, temos que:

Com isso, respondemos a primeira parte do exercício.
Passo 3
Reparou que a última linha de só tem zeros? Isto indica que há uma dependência linear em . Veja que a segunda e a última coluna de são linearmente dependentes: a segunda coluna, , é igual à última coluna, , multiplicada por .
Além disso, a linha de zeros indica que uma das três equações do sistema não ajudaria em nada a encontrar um valor para as incógnitas. Na prática, trata-se de um sistema de 2 equações com 4 incógnitas.
Vamos supor que se tratasse de um sistema de equações onde quiséssemos encontrar os valores de e . A matriz representa esse sistema após alguma manipulações algébricas. O novo sistema teria esta carinha, seguindo os elementos de :
Este sistema tem infinitas soluções. Elas são definidas quando estabelecemos valores para duas incógnitas e usamos as duas equações acima para encontrar as outras duas. Por exemplo, eu podia dizer que e , e, substituindo nas equações acima:
E eu teria e . Claro, essa seria apenas uma das infinitas soluções.
Resposta
O sistema linear representado pela matriz aumentada tem infinitas soluções.
Exercício Resolvido #7
“UNICAMP - Lista de exercícios sobre sistemas lineares de INF903 - INTRODUÇÃO AO MATLAB (2003). Exercício 5”
Escreva aqui o enunciado
Seja a matriz de coeficientes e o lado direito das equações do sistema linear

Entre as matrizes e , e crie a matriz aumentada para este sistema usando o comando do MATLAB . Resolva o sistema usando .
Passo 1
O exercício nos dá um sistema de equações lineares e pede para o resolvermos usando o comando do MATLAB. Contudo, perceba que o sistema tem 4 equações e 3 incógnitas. Isto quer dizer que tem pelo menos uma equação sobrando, que não ajuda a encontrar uma solução para o sistema. O comando vai nos ajudar a ver isso.
Passo 2
O primeiro passo para resolver o exercício é passarmos o sistema de equações para o formato matricial
Onde é uma matriz com os coeficientes das equações, é o vetor com as incógnitas (no caso, , e ) e é o vetor com os valores numéricos à direita do sinal de igual, que não são multiplicados por nenhuma incógnita.
Para o sistema do exercício, temos:
Vamos entrar a matriz e o vetor no MATLAB. Crie um novo script e digite:

Em seguida, vamos criar a matriz aumentada , usando a linha de código:
![]()
Este comando cria uma nova matriz que é uma junção da matriz com o vetor . Basicamente, adicionamos mais uma coluna à , correspondendo a . Fica melhor de visualizar se rodarmos o programa e pedirmos ao MATLAB para imprimir a matriz aumentada :

Repare que as três primeiras colunas de são a matriz e a última coluna, o vetor .
Passo 3
É com a matriz aumentada que encontraremos a solução do sistema linear, usando-a como entrada da função . No seu script do MATLAB, adicione a linha de código:
![]()
Esta linha de código cria a forma escalonada reduzida de , por meio do , e a armazena na variável .
A solução do sistema de equações está na matriz . Rode seu programa e peça ao MATLAB para imprimi-la no Command Window:

Reparou que as duas últimas linhas de só tem zeros? Isto indica que há duas dependências lineares em . Vamos vê-la novamente:

Veja que a segunda e a terceira coluna de são linearmente dependentes: a terceira coluna, , é igual à segunda coluna, , multiplicada por .
Podemos identificar outra dependência linear entre a segunda coluna e a última coluna de : a última coluna, , é igual à segunda coluna, , multiplicada por .
Além disso, as linhas de zeros indicam que duas das quatro equações do sistema não ajudariam em nada a encontrar um valor para as incógnitas. Na prática, trata-se de um sistema de 2 equações com 3 incógnitas.
Se partirmos de para voltar à forma de sistema de equações, temos:
Temos um valor definido para , mas não para e , eles podem assumir qualquer valor, desde que respeitem a equação . Por exemplo, se dissermos que , temos que . Esta é uma dentre as infinitas soluções do sistema.
Logo, este sistema é indeterminado e a segunda equação, , representa essas infinitas soluções.
Resposta
A solução do sistema é:
Exercício Resolvido #8
“Adaptado de An Engineer’s Guide to MATLAB® - With Applications from Mechanical, Aerospace, Electrical, Civil, and Biological Systems Engineering, de Edward B. Magrab, et al, 3ª edição, 2011. Exercício 2.40, p. 124”
Considere dois cilindros longos de materiais diferentes onde um cilindro é encaixado dentro do outro. O raio interno do cilindro interno é e o raio externo, . O raio interno do cilindro externo também é e seu raio externo é . O módulo de Young e o coeficiente de Poisson do cilindro interno são e , respectivamente, e os do cilindro externo são e , respectivamente. A tensão radial , a tensão circunferencial , e o deslocamento radial são dados por:
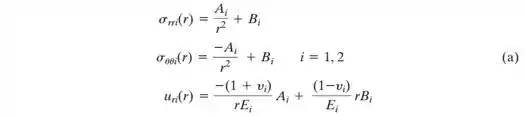
Onde se refere ao cilindro interno e , ao cilindro externo.
Se a superfície externa do cilindro externo é submetida a um deslocamento radial compressivo e a superfície interna do cilindro interno não tem tensões radiais, então as seguintes quatro condições de contorno podem ser usadas para determinar e , :
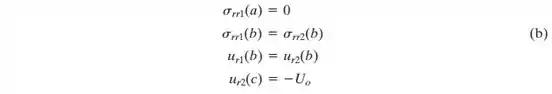
Substituindo as Equações (a) em (b) , o seguinte sistema de equações na forma matricial é obtido:

Determine a tensão circunferencial nos cilindros interno e externo em , considerando , , , , , e .
Passo 1
O enunciado nos dá um sistema de equações lineares na forma matricial, com quatro equações e quatro incógnitas, cuja solução nos dará as constantes , , e , necessárias para o cálculo da tensão circunferencial , dada pela equação:
![]()
O exercício pede para calcular a tensão circunferencial nos cilindros interno e externo em . Para isto, primeiro resolveremos o sistema de equações lineares para obter , , e , usando uma das funções que vimos para resolver sistemas de equações lineares no MATLAB: matriz inversa, barra invertida, ou o .
Com a solução do sistema de equações, podemos calcular a tensão circunferencial de cada cilindro, usando a equação acima e considerando . O cilindro interno é dado por , logo, para calcular sua tensão circunferencial, usaremos e . Já para o cilindro externo, e usaremos e para determinar sua tensão circunferencial.
Passo 2
O sistema de equações lineares no enunciado está no formato matricial:
Onde é uma matriz com os coeficientes das equações, é o vetor com as incógnitas , , e e é o vetor com os valores numéricos à direita do sinal de igual, que não são multiplicados por nenhuma incógnita. Logo, pelo enunciado, temos:
Em um script novo no MATLAB, entre com os dados fornecidos pelo enunciado: os coeficientes de Poisson (representados abaixo por e ), os módulos de Young (representados abaixo por e ), o deslocamento radial compressivo (indicado por abaixo) e os raios , e :
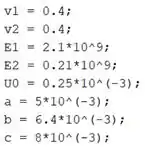
Note que o deslocamento radial e os raios , e foram convertidos de para por meio da multiplicação por . Fazemos isso porque a unidade do módulo de Young está em e para que a unidade da tensão que calcularemos no final também seja em .
Em seguida, entre com a matriz e o vetor :
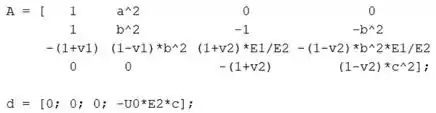
Passo 3
Após definir e , podemos resolver o sistema de equações e encontrar o vetor , representando a solução do sistema.
Vimos quatro formas de resolver um sistema linear no MATLAB: inversão de matriz , barra invertida, e . Você pode usar a forma que quiser, eu escolhi usar a barra invertida:
![]()
Qualquer uma das formas retornará o mesmo vetor . Rode seu programa e ele calculará o vetor como:

Passo 4
Os elementos de são as constantes , , e que servem para calcular a tensão circunferencial , dada pela equação:
![]()
Para facilitar a implementação da equação de para os dois cilindros, vamos armazenar os elementos de em variáveis designando as constantes , , e , por meio das linhas de código:

Na primeira linha, armazenamos o primeiro elemento de na variável , representando a incógnita . Na segunda linha, armazenamos o segundo elemento de na variável , representando a incógnita . e são usados para calcular a tensão circunferencial do cilindro interno.
Na terceira linha, armazenamos o terceiro elemento de na variável , representando a incógnita . Na quarta linha, armazenamos o quarto elemento de na variável , representando a incógnita . e são usados para calcular a tensão circunferencial do cilindro externo.
Tendo feito essas definições, podemos implementar em nosso código a equação que calcula a tensão circunferencial dos dois cilindros, por meio das linhas de código:

Na primeira linha, dizemos que , pois o enunciado pediu que calculássemos a tensão circunferencial nesse valor de raio.
Na segunda linha, calculamos a tensão circunferencial do cilindro interno, designado por , usando a equação de . O resultado é armazenado em .
Na terceira linha, calculamos a tensão circunferencial do cilindro externo, designado por , também usando a equação de . O resultado é armazenado em .
Ao executar o programa, você terá e , que são as tensões circunferenciais nos cilindros interno e externo em :

Resposta
A tensão circunferencial no cilindro interno é:
A tensão circunferencial no cilindro externo é: