Exercícios de Integrais Numéricas - Lista de Exercícios Resolvida

Com o software MATLAB, usando a Regra dos Trapézios, calcule as integrais das seguintes funções:

Seja

Estime pela regra dos trapézios utilizando apenas os valores tabelados abaixo:

A análise do fluxo de um líquido em duto tem aplicação em muitos sistemas diferentes, incluindo o estudo em veias e artérias no corpo humano, o sistema hidráulico de uma cidade, o sistema de irrigação de uma fazenda, o sistema de jato de tinta de uma impressora, etc.

O atrito de um fluxo ao passar num oleoduto circular gera a chamada velocidade de perfil no fluido.

O óleo que está em contato com as paredes do duto não está se movendo na mesma velocidade que o óleo no centro do fluido. O diagrama abaixo mostra como a velocidade do óleo varia de acordo com o diâmetro do duto e define as variáveis usadas para esta análise:

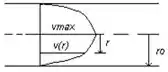
A velocidade de perfil é definida pela seguinte equação:

onde é um número inteiro entre 5 e 10 que define o contorno do escoamento do óleo. A velocidade média de escoamento do óleo pode ser calculada integrando-se a velocidade de perfil no intervalo de a :

Os valores de e de podem ser medidos experimentalmente, e o valor de é o próprio raio do tubo. Escreva um programa no MATLAB para integrar a velocidade de perfil e assim determinar a velocidade média do óleo no duto.

Conside , e .

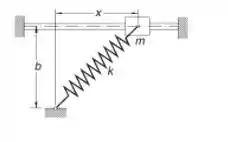
A massa é ligada a uma mola de comprimento livre e rigidez . O coeficiente de atrito entre a massa e a haste horizontal é . A aceleração da massa pode ser demonstrada como , onde

Se a massa é liberada a partir do repouso em , sua velocidade em é dada por

Calcule por meio de integração numérica usando como dados , , , e .

A tabela abaixo mostra a potência fornecida às rodas motrizes de um carro em função da velocidade .

Se a massa do carro é de , determine o intervalo de tempo para que o carro acelere de para . Use o método dos trapézios para a integração. Dica:

que pode ser deduzido a partir da lei de Newton e a definição de potência .

A figura mostra um semi-espaço elástico que carrega um carregamento uniforme de intensidade sobre uma área circular de raio . O deslocamento vertical da superfície no ponto pode ser calculado como

onde é o deslocamento em . Use integração numérica para determinar em .

A tabela abaixo fornece a força do arco em função da distância . Se o arco for puxado , determine a velocidade da flecha de quando ela deixa o arco.

Dica: a energia cinética da flecha é igual ao trabalho realizado ao puxar o arco, isto é:

A fórmula de Debye para a capacidade calorífica de um sólido é , onde

Os termos desta equação são

• número de párticulas no sólido
• constante de Boltzmann
• temperatura absoluta
• temperatura de Debye

Calcule de a em intervalos de e plote os resultados.