Exercícios de Otimização - Lista de Exercícios Resolvida

A figura abaixo mostra um sistema de duas molas com uma carga (representado pelo desenho em linha cheia) e sem carga (desenho em linha tracejada):

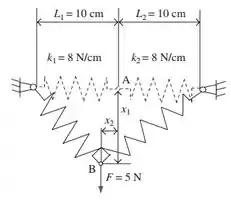
Após a carga ser aplicada no ponto , o sistema se deforma até atingir o equilíbrio no ponto , quando a energia potencial é mínima. A função da energia potencial () é dada pela equação abaixo:

Encontre a localização do ponto onde a energia potencial é mínima de duas maneiras:

1. Plote a superfície e as curvas de nível da função ;
2. Use com um ponto inicial .

Considere o mecanismo de dois pares de barras, mostrado abaixo:

Os elos e têm o mesmo comprimento e os elos e têm o mesmo comprimento . A junta é uma junta fixa, e as juntas e são conexões por pino em duas corrediças que se movem sem atrito ao longo de uma linha horizontal. O mecanismo é submetido a três forças externas. Elas são as forças verticais e nas juntas e , respectivamente, e uma força horizontal na junta . Assume-se que as barras estavam alinhadas e esticadas ao longo de uma linha horizontal antes da aplicação das cargas. Também se assume que o peso do mecanismo é desprezível. O equilíbrio do mecanismo submetido às cargas aplicadas é obtido minimizando a função de energia potencial:

1. Plote a superfície e as curvas de nível da função;
2. Use com ponto inicial radianos para encontrar a energia potencial mínima.

Como achar o mínimo da função com ?

A função

Tem dois mínimos no intervalo . Encontre os valores de e de cada mínimo.

A figura abaixo mostra dois carros A e B conectados por três molas lineares com rigidez igual a , e . Não há atrito no sistema.

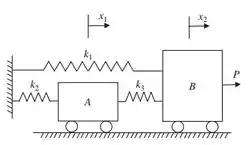
As molas estão em sua posição sem deformação quando a força aplicada é zero. A partir do seguinte problema de otimização para a função da energia potencial :

1. Plote a superfície e as curvas de nível da função;
2. Obtenha os deslocamentos otimizados e usando com ponto inicial e .

A figura abaixo mostra um sistema de molas em posição não-deformada sem cargas (linha tracejada) e em posição deformada com cargas nas juntas entre as molas (linha cheia.)

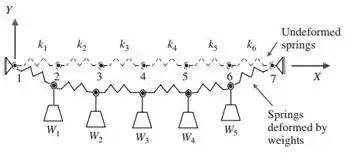
A rigidez da mola é e é definida por:

Onde é o número de cargas. O peso é definido por

O comprimento de cada mola antes da aplicação das cargas é . As coordenadas das juntas das molas (pontos ) são representadas por dez variáveis de projeto: , . Para encontrar a posição de equilíbrio, a seguinte função de energia potencial é minimizada:

Onde

Determine as posições de equilíbrio usando fminsearch, isto é, as posições das juntas para o sistema com as molas deformadas. Use o ponto inicial .

Como achar o máximo da função com ?

Dados os pontos experimentais:

Ajuste os coeficientes () de uma reta () aos dados experimentais.