Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Transformada de Laplace

Ver Todos os Exercícios

Teoria

Introdução

E aí, galera, tudo joia? Não seria legal ter um jeito mais fácil de resolver equações diferenciais? Pois saiba que existe uma forma de converter equações diferenciais em equações algébricas, que em muitos casos vão ser mais fáceis de resolver.

Essa conversão é feita usando a transformada de Laplace, que converte funções como senoides, exponenciais, diferenciais e integrais, normalmente no domínio do tempo t , em funções algébricas no domínio da frequência, em função de uma variável complexa s .

Digamos que você tenha que resolver a seguinte a equação diferencial para encontrar y ( t ) :

a d y d t + y - sin ⁡ t = 0

Para um dado valor inicial y ( 0 ) . Você pode aplicar a transformada de Laplace nela, que dá uma equação algébrica:

a s Y s - a y 0 + Y s - 1 s 2 + 1 = 0

Onde Y ( s ) é a função y ( t ) no domínio s .

Antes, para encontrarmos a função y ( t ) , você teria que usar algum método de solução de equação diferencial, como Runge-Kutta. Com a transformada de Laplace, dá pra isolar Y ( s ) na equação acima:

Y s = 1 a s + 1 1 s 2 + 1 + a y ( 0 )

E aplicar a transformada inversa para voltar à variável t e encontrar y ( t ) . Aqui no Responde Aí, temos uma aula só de transformada de Laplace, caso você queira saber mais como ela funciona.

Usamos muito a transformada de Laplace para programar o controle de sistemas dinâmicos, como um sistema de amortecimento ativo em veículos ou em circuitos elétricos.

O MATLAB tem uma função chamada l a p l a c e ( ) , que determina a transformada de Laplace de uma função, e outra chamada i l a p l a c e ( ) , que determina a tranformada inversa. Na aula de hoje, vamos ver como usar l a p l a c e ( ) e i l a p l a c e ( ) em funções no domínio do tempo f ( t ) ou no domínio da variável s F ( s ) , e como usá-las para resolver equações diferenciais. Partiu?

Transformada de Laplace de uma função f(t)

A função l a p l a c e do MATLAB tem a estrutura:

F = l a p l a c e ( f )

Ela retorna a transformada de Laplace da função f , armazenando-a na variável F .

Digamos que você tenha a função f ( t ) = 2 t e queira encontrar a sua transformada de Laplace usando o MATLAB. Em seu script, defina que t é uma variável simbólica e crie a função f ( t ) = 2 t :

Vamos aplicar l a p l a c e em f   :

Vamos rodar o programa e pedir para o MATLAB mostrar o resultado no Commad Window:

Temos que a transformada de Laplace de f ( t ) = 2 t é F ( s ) = 2 / s ² .

Repare que não precisamos informar que a função de entrada f era em função da variável independente t , nem que queríamos que saída F fosse em função de s . É que, por padrão, o MATLAB considera que f depende de uma variável t e que a variável da transformada F é s . Você pode alterar isso adicionando mais entradas à função l a p l a c e :

F = l a p l a c e ( f , v a r _ i n d e p e n d e n t e , v a r _ l a p l a c e   )

Com este comando, dizemos que a função f tem como variável independente o que pusermos no lugar de v a r _ i n d e p e n d e n t e . A transformada F gerada pelo MATLAB será em função do que pusermos no lugar de v a r _ l a p l a c e .

Por exemplo, digamos que você queira encontrar a transformada de Laplace da função:

f a = e - t a

Sendo que a é a variável independente de f ( a ) .

Além disso, você quer que a transformada de Laplace de f ( a ) seja em função de y . Por isso, você terá que usar a função l a p l a c e no MATLAB como no print abaixo:

Na primeira linha, criamos as variáveis simbólicas a , t e y .

Na segunda linha, criamos a função f a = e - t a .

Na terceira linha, usamos l a p l a c e ( f , a , y ) para encontrar a transformada de Laplace de f . Perceba que no lugar de v a r _ i n d e p e n d e n t e , coloquei a ; e que no lugar de v a r _ l a p l a c e , coloquei y . Isto quer dizer que a saída F será em função de y .

Rodando o programa, temos:

Inversa da transformada de Laplace de uma função F(s)

Digamos que agora você tem uma função no domínio da frequência s e quer encontrá-la no domínio do tempo t . Você pode usar a função do MATLAB i l a p l a c e , que calcula a inversa da transformada de Laplace de uma função. Ela tem o formato:

f = i l a p l a c e ( F )

Ela retorna a inversa da transformada de Laplace da função F , armazenando-a na variável f .

Vamos de exemplo. Temos a função no domínio da frequência:

F ( s ) = 2 s ²

E queremos encontrá-la no domínio do tempo t usando o MATLAB. Para isso, digite em um novo script as linhas de código:

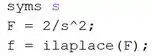
Na primeira linha, definimos a variável simbólica s .

Na segunda linha, entramos com a função F ( s ) = 2 / s ² .

Na terceira linha, aplicamos i l a p l a c e ( F ) para encontrar a inversa da transformada de Laplace de F .

Rodando o programa, temos como resultado:

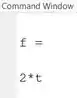
Temos que a inversa da transformada de Laplace de F ( s ) = 2 / s ² é f ( t ) = 2 t . Reparou que é o mesmo exemplo da seção anterior? =)

Assim como na função l a p l a c e , por padrão, em i l a p l a c e , o MATLAB considera que f depende de uma variável independente t e que a variável da transformada F é s . Você também pode alterar isso adicionando mais entradas à função i l a p l a c e :

f = i l a p l a c e ( F , v a r _ i n d e p e n d e n t e , v a r _ i n v _ l a p )

Com este comando, dizemos que a função F tem como variável independente o que pusermos no lugar de v a r _ i n d e p e n d e n t e . A inversa da transformada de Laplace f gerada pelo MATLAB será em função do que pusermos no lugar de v a r _ i n v _ l a p .

Transformada de Laplace para resolver uma equação diferencial

Vimos como usar l a p l a c e em funções f ( t ) . Agora vamos ver como usamos transformada de Laplace para resolver equações diferenciais. Lembram daquela equação diferencial do começo da aula? Essa aqui:

a d y d t + y - sin ⁡ t = 0

Vamos encontrar uma solução para y ( t ) usando as funções l a p l a c e e i l a p l a c e . Primeiramente, vamos entrar com a equação diferencial em um novo script do MATLAB:

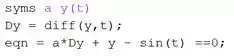
Na primeira linha, definimos as variáveis simbólicas a e y ( t ) (indicamos que y é em função de t ).

Na segunda linha, calculamos a derivada d y d t usando a função d i f f ( y , t ) do MATLAB. Como estamos trabalhando com variáveis simbólicas, d i f f ( y , t ) calcula a derivada de y em relação a t e armazena a resposta em D y . Como a função y não é conhecida, se pedirmos ao MATLAB para nos mostrar D y , ele indicará:

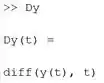
Na terceira linha, criamos uma variável e q n que armazena a equação diferencial.

Vamos aplicar l a p l a c e em e q n para transformar a equação diferencial em uma equação algébrica, armazenada em E :

Vamos ver como ficou? Rode o programa e peça ao MATLAB para imprimir no Command Window a variável E :

Perceba que o MATLAB usa l a p l a c e ( y ( t ) , t , s ) em alguns elementos de E , que tem exatamente a mesma estrutura da função l a p l a c e . Essa expressão representa a transformada de Laplace de y ( t ) e pode ser substituída por Y ( s ) . Logo, o resultado seria assim:

Y s - a y 0 - s Y s - 1 s 2 + 1 = 0

Esse E ficou meio comprido, né? Podemos substituir l a p l a c e ( y ( t ) , t , s ) por Y , representando Y ( s ) , usando o comando s u b s :

Primeiramente, devemos criar mais duas variáveis simbolicas: s e Y . Em seguida, usamos a função s u b s para pedir ao MATLAB que substitua em E a expressão l a p l a c e ( y ( t ) , t , s ) por Y . O resultado da substituição é armazenado em E , ficando no lugar aquela expressão comprida que vimos.

Após a substituição, E fica assim:

Para encontrar y ( t ) , precisamos encontrar Y ( s ) para daí aplicar nela a inversa da tranformada de Laplace. Em E , a variável Y representa Y ( s ) e podemos usar a função s o l v e do MATLAB para encontrá-la. Adicione em seu código:

Com este comando, a função s o l v e resolve a equação E para a variável Y e armazena a solução em L . Na prática, isolamos Y na equação com este comando e L representa Y ( s ) . Rodando o programa, temos que L é igual a:

Isto quer dizer que:

L = Y s = a y 0 + 1 s 2 + 1 a s + 1 = 1 a s + 1 1 s 2 + 1 + a y ( 0 )

Para encontrar y ( t ) , aplicamos a inversa da transformada de Laplace em Y ( s ) , isto é, usamos i l a p l a c e em L :

O resultado é armazenado em I . Na prática, I = y ( t ) , logo, quando rodarmos o programa, encontraremos y ( t ) .

Temos que I é igual a:

A expressão acima corresponde a y ( t ) , logo, encontramos a solução da equação diferencial.

E aí? Curtiu a aula de hoje? Além de aprendermos a usar l a p l a c e e i l a p l a c e , vimos de quebra outras funçõesinhas do MATLAB, como s u b s e s o l v e . Agora bora fazer os exercícios para fixar bem o conteúdo ;D

Transformada de Laplace de uma função f(t)

Inversa da transformada de Laplace de uma função F(s)

Transformada de Laplace para resolver uma equação diferencial

Exercícios Resolvidos

Exercício Resolvido #1

“USP – Departamento de Engenharia Elétrica e Computação – 2016 Brazil Study Abroad Program – Texas A&M University – University of São Paulo”

Usando o MATLAB, calcule a transformada de Laplace de f ( t ) = c o s ( w t ) .

Passo 1

O exercício pede para encontrarmos a transformada de Laplace da função f ( t ) = c o s ( w t ) usando o MATLAB. Logo, usaremos a função l a p l a c e ( ) neste exercício.

Como o enunciado não especificou nada, consideraremos que a variável independente de f ( t ) é t e que a transformada de Laplace da função será em função de s , que é o padrão adotado pelo MATLAB. Em outras palavras, a transformada de Laplace de f ( t ) será representada por F ( s ) .

Passo 2

Antes de partirmos para o MATLAB, vamos relembrar como é a função l a p l a c e . A função l a p l a c e do MATLAB tem a estrutura:

F = l a p l a c e ( f )

Ela retorna a transformada de Laplace da função f , armazenando-a na variável F . Como não tem mais nenhuma entrada em l a p l a c e além de f , o MATLAB assumirá que a variável independente de f é t e fará que a transformada de Laplace F seja em função de s .

Em um novo script do MATLAB, entre com a função f ( t ) = c o s ( w t ) :

Na primeira, definimos duas variáveis simbólicas: w e t .

Na segunda linha, entramos com a função f ( t ) = c o s ( w t ) , que é armazenada na variável f .

Passo 3

Após ter entrado com f ( t ) , vamos usar l a p l a c e para encontrar a transformada de Laplace de f :

A transformada de Laplace de f é armazenada na variável F .

Rode o programa para ver como fica F :

Resposta

A transformada de Laplace de f ( t ) = c o s ( w t ) é:

F ( s ) = s s 2 + w ²

Exercício Resolvido #2

“USP – Departamento de Engenharia Elétrica e Computação – 2016 Brazil Study Abroad Program – Texas A&M University – University of São Paulo”

Usando o MATLAB, calcule a transformada de Laplace de:

  1. Degrau unitário u ( t ) ;
  2. Impulso unitário δ ( t ) .

Passo 1

O exercício pede para encontrarmos a transformada de Laplace, usando o MATLAB, de duas funções muito utilizadas na área de controle: a função degrau unitário e a função impulso unitário.

Para criarmos a função degrau unitário no MATLAB, usaremos a função h e a v i s i d e ( ) . Já para a função impulso, usaremos a função d i r a c ( ) . Essa deve ser a primeira vez que você vê essas funções, mas não se preocupe, vamos ver direitinho como elas funcionam. Ao final, usaremos a função l a p l a c e ( ) para encontrar as transformadas de u ( t ) e δ ( t ) .

Como o enunciado não especificou nada, consideraremos que a variável independente de u ( t ) e δ ( t ) é t e que a transformada de Laplace delas será em função de s , que é o padrão adotado pelo MATLAB. Em outras palavras, a transformada de Laplace de u ( t ) e δ ( t ) será representada por U ( s ) e D ( s ) , respectivamente.

Passo 2

Vamos começar pela letra a. Para criarmos o degrau unitário u ( t ) no MATLAB, usaremos a função h e a v i s i d e , que tem a estrutura:

u = h e a v i s i d e ( t )

Ela cria um degrau unitário e o armazena em u : quando t   <   0 , u = 0 . Se t = 0 , u = 1 / 2 . Finalmente, para t >   0 , u = 1 .

Em um script novo, digite as duas linhas de código:

Na primeira linha, criamos a variável simbólica t .

Na segunda linha, usamos a função h e a v i s i d e para criar o degrau unitário, que é armazenado em u . Como t é uma variável simbólica, se você rodar o programa e pedir pra ver u , o MATLAB vai te retornar isso:

Como não foi definido se t é maior, menor ou igual a 0 , o MATLAB vai armazenar em u a função h e a v i s i d e ( t ) mesmo.

Passo 3

Após criar o degrau unitário, podemos achar sua transformada de Laplace usando o comando l a p l a c e , que tem a estrutura:

F = l a p l a c e ( f )

Ela retorna a transformada de Laplace da função f , armazenando-a na variável F . Como não tem mais nenhuma entrada em l a p l a c e além de f , o MATLAB assumirá que a variável independente de f é t e fará que a transformada de Laplace F seja em função de s .

Adicione ao seu script o comando:

Ele vai calcular a transformada de Laplace de u e vai armazenar o resultado em U .

Vamos ver a carinha de U ? Rode o programa e você terá:

Pronto! Letra a concluída.

Passo 4

Vamos fazer a letra b. Para criarmos o impulso unitário δ ( t ) no MATLAB, usaremos a função d i r a c , que tem a estrutura:

d = d i r a c ( t )

No MATLAB, d i r a c calcula o delta de Dirac de t , que basicamente diz que pra qualquer valor t ≠ 0 , d = 0 . Já para t = 0 , d = ∞ . Logo, isso representa matematicamente um sinal de impulso.

Em um novo script do MATLAB, digite as duas linhas de código:

Na primeira linha, criamos a variável simbólica t .

Na segunda linha, usamos a função d i r a c para criar o impulso unitário, que é armazenado em d . Como t é uma variável simbólica, se você rodar o programa e pedir pra ver d , o MATLAB vai te retornar isso:

Como não foi definido se t é igual ou diferente a 0 , o MATLAB vai armazenar em d a função d i r a c ( t ) mesmo.

Passo 5

Após criar a função impulso d , vamos usar l a p l a c e para encontrar a transformada de Laplace de d , adicionando no código o comando:

A transformada de Laplace de d é armazenda na variável D .

Ao rodarmos o programa, vemos que a transformada de Laplace do impulso unitário é:

Resposta

  1. A transformada de Laplace de u ( t ) é

    2. U s = 1 s

  2. A transformada de Laplace de δ ( t ) é

D s = 1

Exercício Resolvido #3

“USP – Departamento de Engenharia Elétrica e Computação – 2016 Brazil Study Abroad Program – Texas A&M University – University of São Paulo”

Usando o MATLAB, calcule a inversa da transformada de Laplace de

F s = 1 s + a 2

Passo 1

O exercício pede para encontrarmos a inversa da transformada de Laplace F ( s ) = 1 / s + a 2 usando o MATLAB. Logo, usaremos a função i l a p l a c e ( ) neste exercício.

Como o enunciado não especificou nada, consideraremos que a variável independente de F ( s ) é s e que a sua inversa será em função de t , que é o padrão adotado pelo MATLAB. Em outras palavras, a inversa da transformada de Laplace F ( s ) será representada por   f ( t ) .

Passo 2

Antes de partirmos para o MATLAB, vamos relembrar como é a função i l a p l a c e . A função i l a p l a c e do MATLAB tem a estrutura:

f = i l a p l a c e ( F )

Ela retorna a inversa da transformada de Laplace de F , armazenando-a na variável f . Como não tem mais nenhuma entrada em i l a p l a c e além de F , o MATLAB assumirá que a variável independente de F é s e fará que a inversa da transformada de Laplace f seja em função de t .

Em um novo script do MATLAB, entre com a função F ( s ) dada no enunciado:

Na primeira linha, criamos duas variáveis simbólicas: s e a .

Na segunda linha, entramos com a função F ( s ) dada pelo enunciado, armazenando-a na variável F .

Passo 3

Após ter entrado com F ( s ) , vamos usar i l a p l a c e para encontrar a inversa da transformada de Laplace de F :

A inversa da transformada de Laplace de F é armazenada na variável f .

Rode o programa para ver qual é a cara de f :

Resposta

A inversa da transformada de Laplace F ( s ) = 1 / s + a 2 é f t = t e - a t .

Exercício Resolvido #4

“Elaboração Própria”

Usando as funções l a p l a c e e i l a p l a c e do MATLAB, encontre y ( t ) resolvendo a equação diferencial abaixo:

d ² y d t ² + 2 ξ d y d t + y = u ( t )

Onde u ( t ) é a função degrau unitário. Considere y ( 0 ) = 0 e d y ( 0 ) / d t = 0 .

Passo 1

O exercício pede para encontrarmos a solução y ( t ) de uma equação diferencial de segunda ordem, usando transformada de Laplace. Primeiramente, aplicaremos a função l a p l a c e do MATLAB na equação diferencial para encontrarmos a transformade de y ( t ) . Como o enunciado não especificou nada, consideraremos que a variável independente das transformadas de Laplace é s , que é o padrão do MATLAB. Logo, a transformada de Laplace de y ( t ) será Y ( s ) .

Após encontrarmos Y ( s ) , vamos aplicar i l a p l a c e para encontrar a inversa da transformada, isto é, y ( t ) , que é a solução da equação diferencial.

Passo 2

Vamos começar entrando com a equação diferencial no MATLAB, termo a termo. Em um script novo, digite as linhas de código:

Na primeira linha, criamos duas variáveis simbólicas: c s i (representando a letra grega ξ ) e y ( t ) (indicamos que y é em função de t ).

Na segunda linha, calculamos a derivada d y d t usando a função d i f f ( y , t ) do MATLAB. Como estamos trabalhando com variáveis simbólicas, d i f f ( y , t ) calcula a derivada de y em relação a t e armazena a resposta em D y . Como a função y não é conhecida, se pedirmos ao MATLAB para nos mostrar D y , ele indicará:

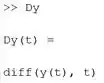
Na terceira linha, calculamos a derivada d ² y d t ² , pedindo ao MATLAB para calcular a derivada de D y em função de t ( d i f f ( D y , t ) ).

Na quarta linha, criamos um degrau unitário u em função de t usando a função h e a v i s i d e ( t ) .

Tendo definido os termos da equação, vamos criá-la e armazená-la na variável e q n :

Perceba que joguei o degrau unitário u para o lado esquerdo da equação, e deixei tudo igual a 0 .

Passo 3

Com a equação diferencial no MATLAB, podemos usar a função l a p l a c e para calcular a transformada de Laplace dela. Lembrando que l a p l a c e tem como estrutura:

F = l a p l a c e ( f )

Ela retorna a transformada de Laplace da função f , armazenando-a na variável F . Quando não tem mais nenhuma entrada em l a p l a c e além de f , o MATLAB assume que a variável independente de f é t e fará que a transformada de Laplace F seja em função de s .

Acrescente em seu programa o comando abaixo para calcular a transformada de Laplace de e q n :

O resultado é armazenado em E .

Vamos ver como ficou E ? Rodando o programa que fizemos até agora, temos:

Nossa, ficou bem grandinho, né? Pra caber na página, tive que deixar a letra beeeem pequeninha.

Vamos resolver isso fazendo umas substituições. Perceba que o MATLAB usa l a p l a c e ( y ( t ) , t , s ) em alguns elementos de E , que tem exatamente a mesma estrutura da função l a p l a c e . Essa expressão representa a transformada de Laplace de y ( t ) e pode ser substituída por Y ( s ) . No caso, chamaremos Y ( s ) só de Y .

Adicione os comandos abaixo em seu programa para fazer a substituição:

Primeiramente, devemos criar mais duas variáveis simbolicas: s e Y . Em seguida, usamos a função s u b s para pedir ao MATLAB que substitua em E a expressão l a p l a c e ( y ( t ) , t , s ) por Y . O resultado da substituição é armazenado em E , ficando no lugar aquela expressão comprida que vimos.

Após a susbtituição, E fica assim:

Note que tem mais coisa pra substituir aí. O enunciado disse para considerarmos y ( 0 ) = 0 e d y ( 0 ) / d t = 0 . O y ( 0 ) é fácil de achar ali em cima, mas e o d y ( 0 ) / d t ? Ele é representado por s u b s ( d i f f ( y ( t ) ,   t ) ,   t ,   0 ) .

Para fazer as substituições, adicione ao seu programa as duas linhas de código:

Na primeira linha, substituímos y ( 0 ) por 0 em E e armazenamos a nova expressão em E , no lugar daquele E mais comprido.

Na segunda linha, substituímos s u b s ( d i f f ( y ( t ) ,   t ) ,   t ,   0 ) por 0 , isto é, fazemos que d y ( 0 ) / d t = 0 , no E gerado na linha anterior. A nova expressão é armazenada em E , no lugar da anterior.

Executando o programa, podemos ver como E está agora:

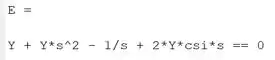
Bem mais enxuta, né?

Passo 4

Para encontrar y ( t ) , precisamos encontrar Y ( s ) para daí aplicar nela i l a p l a c e , para termos a inversa da tranformada de Laplace. Em E , a variável Y representa Y ( s ) e podemos usar a função s o l v e do MATLAB para encontrá-la. Adicione em seu código:

Com este comando, a função s o l v e resolve a equação E para a variável Y e armazena a solução em Y , atualizando seu valor. Na prática, isolamos Y na equação com este comando e Y passa a representar a expressão algébrica de Y ( s ) . Rodando o programa, temos que Y é igual a:

Quer dizer que:

Y s = 1 s 3 + 2 ξ s 2 + s

Para encontrarmos y ( t ) , devemos aplicar a inversa da transformada de Laplace em Y ( s ) , isto é, usar a função i l a p l a c e do MATLAB em Y . A função i l a p l a c e tem a estrutura:

f = i l a p l a c e ( F )

Ela retorna a inversa da transformada de Laplace de F , armazenando-a na variável f . Quando não tem mais nenhuma entrada em i l a p l a c e além de F , o MATLAB assume que a variável independente de F é s e fará que a inversa da transformada de Laplace f seja em função de t .

Para encontrar y ( t ) , entre o comando:

Com este comando, o MATLAB calcula a inversa da transformada de Laplace de Y e armazena o resultado em y , atualizando seu valor. y é a solução da equação diferencial.

Rodando o programa, temos que y é igual a:

Resposta

y t = 1 - e - ξ t cosh ⁡ t ξ 2 - 1 + ξ sinh ⁡ t ξ 2 - 1 t ξ 2 - 1

Exercício Resolvido #5

“Adaptado de MATLAB® for Engineering Applications, de William J. Palm III, McGraw-Hill Education, 4ª edição, 2019. Exemplo T11.5-2, p. 493”

Use a transformada de Laplace para resolver o problema:

5 y ¨ + 20 y ˙ + 15 y = 30 u - 4 u ˙

Onde u ( t ) é a função degrau unitário e y ( 0 ) = 5 , y ˙ ( 0 ) = 1 .

Passo 1

O exercício pede para encontrarmos a solução y de uma equação diferencial de segunda ordem, usando transformada de Laplace. Primeiramente, aplicaremos a função l a p l a c e do MATLAB na equação diferencial para encontrarmos a transformada de y .

Consideraremos que y é em função de t , pois a função degrau dada no enunciado é apresentada como u ( t ) .

Como o enunciado não especificou nada, consideraremos que a variável independente das transformadas de Laplace é s , que é o padrão do MATLAB. Logo, a transformada de Laplace de y ( t ) será Y ( s ) .

Após encontrarmos Y ( s ) , vamos aplicar i l a p l a c e para encontrar a inversa da transformada, isto é, y ( t ) , que é a solução da equação diferencial.

Passo 2

Vamos começar entrando com a equação diferencial no MATLAB, termo a termo. Em um script novo, digite as linhas de código:

Na primeira linha, criamos a variável simbólicas y ( t ) , indicamos que y é em função de t .

Na segunda linha, calculamos a derivada y ˙ usando a função d i f f ( y , t ) do MATLAB. Como estamos trabalhando com variáveis simbólicas, d i f f ( y , t ) calcula a derivada de y em relação a t e armazena a resposta em D y . Como a função y não é conhecida, se pedirmos ao MATLAB para nos mostrar D y , ele indicará:

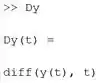
Na terceira linha, calculamos a derivada y ¨ , pedindo ao MATLAB para calcular a derivada de D y em função de t ( d i f f ( D y , t ) ).

Na quarta linha, criamos um degrau unitário u em função de t usando a função h e a v i s i d e ( t ) .

Na quinta linha, calculamos a primeira derivada do degrau unitário u ˙ usando d i f f ( u , t ) . A derivada é armazenada em D u .

Tendo definido os termos da equação, vamos criá-la e armazená-la na variável e q n :

Perceba que joguei os termos 30 u e - 4 u ˙ para o lado esquerdo da equação e fiz que tudo é igual a 0 .

Passo 3

Com a equação diferencial no MATLAB, podemos usar a função l a p l a c e para calcular a transformada de Laplace dela. Lembrando que l a p l a c e tem como estrutura:

F = l a p l a c e ( f )

Ela retorna a transformada de Laplace da função f , armazenando-a na variável F . Quando não tem mais nenhuma entrada em l a p l a c e além de f , o MATLAB assume que a variável independente de f é t e fará que a transformada de Laplace F seja em função de s .

Acrescente em seu programa o comando abaixo para calcular a transformada de Laplace de e q n :

O resultado é armazenado em E .

Vamos ver como ficou E ? Rodando o programa que fizemos até agora, temos:

Nossa, ficou bem grandinho, né? Pra caber na página, tive que deixar a letra beeeem pequeninha.

Vamos resolver isso fazendo umas substituições. Perceba que o MATLAB usa l a p l a c e ( y ( t ) , t , s ) em alguns elementos de E , que tem exatamente a mesma estrutura da função l a p l a c e . Essa expressão representa a transformada de Laplace de y ( t ) e pode ser substituída por Y ( s ) . No caso, chamaremos Y ( s ) só de Y .

Adicione os comandos abaixo em seu programa para fazer a substituição:

Primeiramente, devemos criar mais duas variáveis simbolicas: s e Y . Em seguida, usamos a função s u b s para pedir ao MATLAB que substitua em E a expressão l a p l a c e ( y ( t ) , t , s ) por Y . O resultado da substituição é armazenado em E , ficando no lugar aquela expressão comprida que vimos.

Após a susbtituição, E fica assim:

Ainda tem mais coisa pra substituir aí. O enunciado disse para considerarmos y ( 0 ) = 5 e y ˙ ( 0 ) = 1 . O y ( 0 ) é fácil de achar ali em cima, mas e o y ˙ ( 0 ) ? Ele é representado por s u b s ( d i f f ( y ( t ) ,   t ) ,   t ,   0 ) .

Para fazer as substituições, adicione ao seu programa as duas linhas de código:

Na primeira linha, substituímos y ( 0 ) por 5 em E e armazenamos a nova expressão novamente em E , no lugar daquele E mais comprido.

Na segunda linha, substituímos s u b s ( d i f f ( y ( t ) ,   t ) ,   t ,   0 ) por 1 , isto é, fazemos que y ˙ ( 0 ) = 1 , no E gerado na linha anterior. A nova expressão é armazenada em E , no lugar da anterior.

Executando o programa, podemos ver como E está agora:

Bem mais bonitinha, né?

Passo 4

Para encontrar y ( t ) , precisamos encontrar Y ( s ) para daí aplicar nela i l a p l a c e , para termos a inversa da tranformada de Laplace. Em E , a variável Y representa Y ( s ) e podemos usar a função s o l v e do MATLAB para encontrá-la. Adicione em seu código:

Com este comando, a função s o l v e resolve a equação E para a variável Y e armazena a solução em Y , atualizando seu valor. Na prática, isolamos Y na equação com este comando e Y passa a representar a expressão algébrica de Y ( s ) . Rodando o programa, temos que Y é igual a:

Quer dizer que:

Y s = 25 s + 30 s + 101 5 s 2 + 2 0 s + 15

Para encontrarmos y ( t ) , demos aplicar a inversa da transformada de Laplace em Y ( s ) , isto é, usar a função i l a p l a c e do MATLAB em Y . A função i l a p l a c e tem a estrutura:

f = i l a p l a c e ( F )

Ela retorna a inversa da transformada de Laplace de F , armazenando-a na variável f . Quando não tem mais nenhuma entrada em i l a p l a c e além de F , o MATLAB assume que a variável independente de F é s e fará que a inversa da transformada de Laplace f seja em função de t .

Para encontrar y ( t ) , entre o comando:

Com este comando, o MATLAB calcula a inversa da transformada de Laplace de Y e armazena o resultado em y , atualizando seu valor. y é a solução da equação diferencial.

Rodando o programa, temos que y é igual a:

Podemos transformar as frações, como 23 / 5 , em números decimais, usando o comando v p a do MATLAB. Este elemento avalia cada elemento de uma expressão simbólica e identifica as frações com números reais, e as transforma em números “quebrados”.

Acrescente no seu código o comando:

Este comando aplica a função v p a em y e armazena o resultado em y , substituindo a expressão anterior. Ao rodar programa, podemos ver y com seus coeficientes transformados em números decimais:

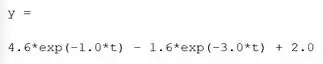
Resposta

y t = 4,6 e - t - 1,6 e - 3 t + 2

Exercício Resolvido #6

“Adaptado de MATLAB® for Engineering Applications, de William J. Palm III, McGraw-Hill Education, 4ª edição, 2019. Exercício 45, p. 558”

A equação diferencial que modela o torque m ( t ) de um motor exigido para um certo sistema de controle de velocidade é

4 m ¨ + 4 K m ˙ + K 2 m = K 2 v ˙ d

Onde v d ( t ) é a velocidade desejada e K é uma constante chamada “ganho”.

Use o método da transformada de Laplace para encontrar a resposta ao degrau unitário (isto é, v d ( t ) é uma função degrau unitário). Use condições iniciais nulas.

Passo 1

O exercício pede para encontrarmos a resposta do torque m ( t ) a v d ( t ) igual a um degrau unitário, usando a transformada de Laplace. Em outras palavras, vamos encontrar a solução m da equação diferencial de segunda ordem dada pelo enunciado. Primeiramente, aplicaremos a função l a p l a c e do MATLAB na equação diferencial para encontrarmos a transformada de m .

Como o enunciado não especificou nada, consideraremos que a variável independente das transformadas de Laplace é s , que é o padrão do MATLAB. Logo, a transformada de Laplace de m ( t ) será M ( s ) .

Após encontrarmos M ( s ) , vamos aplicar i l a p l a c e para encontrar a inversa da transformada, isto é, m ( t ) , que é a solução da equação diferencial.

Passo 2

Vamos começar entrando com a equação diferencial no MATLAB, termo a termo. Em um script novo, digite as linhas de código:

Na primeira linha, criamos as variáveis simbólicas K e m ( t ) , indicando que m é em função de t .

Na segunda linha, calculamos a derivada m ˙ usando a função d i f f ( m , t ) do MATLAB. Como estamos trabalhando com variáveis simbólicas, d i f f ( m , t ) apenas representa a derivada de m em relação a t e é armazenado em D m .

Na terceira linha, calculamos a derivada m ¨ , pedindo ao MATLAB para calcular a derivada de D m em função de t ( d i f f ( D m , t ) ).

Na quarta linha, criamos um degrau unitário v _ d em função de t usando a função h e a v i s i d e ( t ) , representando a velocidade desejada do motor.

Na quinta linha, definimos a primeira derivada do degrau unitário v ˙ d usando d i f f ( v _ d , t ) . A derivada é armazenada em D v _ d .

Tendo definido os termos da equação, vamos criá-la e armazená-la na variável e q :

Note que joguei todos os termos da equação diferencial para a esquerda, e que fiz tudo igual a 0 .

Passo 3

Com a equação diferencial no MATLAB, podemos usar a função l a p l a c e para calcular a transformada de Laplace dela. Lembrando que l a p l a c e tem como estrutura:

F = l a p l a c e ( f )

Ela retorna a transformada de Laplace da função f , armazenando-a na variável F .

Acrescente em seu programa o comando abaixo para calcular a transformada de Laplace de e q :

O resultado é armazenado em E . Vamos ver como ele ficou? Rode o programa que fizemos até agora e imprima E no Command Window:

Ficou um expressão bem comprida, tá até difícil de ler.

Vamos resolver isso fazendo umas substituições. Perceba que o MATLAB usa l a p l a c e ( m ( t ) , t , s ) em alguns elementos de E , que tem exatamente a mesma estrutura da função l a p l a c e . Essa expressão representa a transformada de Laplace de m ( t ) e pode ser substituída por M ( s ) . No caso, chamaremos M ( s ) só de M .

Adicione os comandos abaixo em seu programa para fazer a substituição:

Primeiramente, devemos criar mais duas variáveis simbolicas: s e M . Em seguida, usamos a função s u b s para pedir ao MATLAB que substitua em E a expressão l a p l a c e ( m ( t ) , t , s ) por M . O resultado da substituição é armazenado em E , substituindo a expressão anterior. Após a susbtituição, E fica assim:

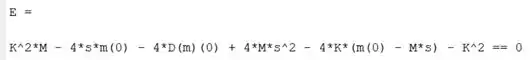
Melhorou bastante, né? Agora vamos substituir as condições iniciais em E . O enunciado disse que elas são nulas, logo, m 0 = m ˙ 0 = 0 . Na expressão acima, é fácil de identificar quem é m ( 0 ) . Já m ˙ 0 é representado por D ( m ) ( 0 ) .

Para fazer as substituições, adicione ao seu programa a linha de código:

Com este comando, substituímos em E m ( 0 ) e D ( m ) ( 0 ) por 0 e armazenamos a nova expressão em E , no lugar da antiga. Note que usei aspas simples em ' D ( m ) ( 0 ) ' . Elas servem para indicar que é uma expressão só. Se você tentar rodar o programa sem elas, o MATLAB acusará erro de sintaxe.

Vamos ver a nova cara de E :

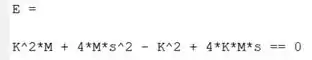
Passo 4

Agora podemos encontrar m ( t ) . Para isto, precisamos encontrar M ( s ) para daí aplicar nele i l a p l a c e , para termos a inversa da tranformada de Laplace. Em E , a variável M representa M ( s ) e podemos usar a função s o l v e do MATLAB para encontrá-la. Adicione em seu código:

Com este comando, a função s o l v e resolve a equação E para a variável M e armazena a solução em M , atualizando seu valor. Na prática, isolamos M na equação com este comando e M passa a representar a expressão algébrica de M ( s ) . Rodando o programa, temos que M é igual a:

Passo 5

Para encontrarmos m ( t ) , devemos aplicar a inversa da transformada de Laplace em M ( s ) , isto é, usar a função i l a p l a c e do MATLAB em M . A função i l a p l a c e tem a estrutura:

f = i l a p l a c e ( F )

Ela retorna a inversa da transformada de Laplace de F , armazenando-a na variável f .

Para encontrar m ( t ) , entre o comando:

Com este comando, o MATLAB calcula a inversa da transformada de Laplace de M e armazena o resultado em m , atualizando seu valor. m é a solução da equação diferencial, representadno a resposta do sistema ao degrau unitário. Rodando o programa, temos que m é igual a:

Resposta

A resposta ao degrau unitário é:

m t = K 2 t e - K t 2 4

Exercício Resolvido #7

“Adaptado de MATLAB® for Engineering Applications, de William J. Palm III, McGraw-Hill Education, 4ª edição, 2019. Exercício 42, p. 556”

O circuito RLC abaixo pode ser usado como um filtro de banda estreita. Se a tensão de entrada v i ( t ) consiste na soma de tensões de variação sinusoidal com diferentes frequências, o filtro de banda estreita permitirá passar somente tensões cujas frequências estão dentro de uma faixa estreita. Esses filtros são usados em circuitos de sintonia, como os usados em rádios AM, para permitir a recepção apenas do sinal portador da estação de rádio desejada.

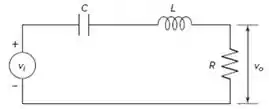
O circuito RLC tem a seguinte equação diferencial:

L C v ¨ 0 + R C v ˙ 0 + v 0 = R C v ˙ i ( t )

Onde v 0 ( t ) é a tensão de saída.

Use o método da transformada de Laplace para encontrar a resposta ao degrau unitário de v 0 ( t ) para condições iniciais nulas, onde C = 10 ∙ 10 - 5   F e L = 5 ∙ 10 - 3   H . Para modelar um filtro de banda larga, use R = 1000   Ω . Já para modelar um filtro de banda estreita, use R = 10   Ω . Compare a resposta ao degrau dos dois casos.

Passo 1

O exercício pede para encontrarmos a resposta de v 0 ( t ) a v i ( t ) igual a um degrau unitário, usando a transformada de Laplace. Em outras palavras, vamos encontrar a solução v 0 da equação diferencial de segunda ordem dada pelo enunciado. Primeiramente, aplicaremos a função l a p l a c e do MATLAB na equação diferencial para encontrarmos a transformada de v 0 . A transformada de Laplace de v 0 ( t ) será indicada por V 0 ( s ) .

Após encontrarmos V 0 ( s ) , vamos aplicar i l a p l a c e para encontrar a inversa da transformada, isto é, v 0 ( t ) , que é a solução da equação diferencial.

Vamos fazer esse procedimento considerando C , L e R simbólicos, substituindo-os pelos valores dados pelo enunciado somente no final. Para compararmos a resposta ao degrau, substituiremos em v 0 ( t ) os dois valores de R e veremos como ficará a expressão simbólica para ambos os casos.

Passo 2

Comece entrando com a equação diferencial no MATLAB, termo a termo. Em um script novo, digite as linhas de código:

Na primeira linha, criamos as variáveis simbólicas L , C , R e v _ 0 ( t ) , indicando que v _ 0 é em função de t .

Na segunda linha, calculamos a derivada v ˙ 0 usando a função d i f f ( v _ 0 , t ) do MATLAB. Como estamos trabalhando com variáveis simbólicas, d i f f ( v _ 0 , t ) apenas representa a derivada de v _ 0 em relação a t e é armazenado em D v _ 0 .

Na terceira linha, calculamos a derivada v ¨ 0 , pedindo ao MATLAB para calcular a derivada de D v _ 0 em relação a t ( d i f f ( D v _ 0 , t ) ).

Na quarta linha, criamos um degrau unitário v _ i em função de t usando a função h e a v i s i d e ( t ) , representando a tensão de entrada do circuito.

Na quinta linha, definimos a primeira derivada do degrau unitário v ˙ i usando d i f f ( v _ i , t ) . A derivada é armazenada em D v _ i .

Tendo definido os termos da equação, vamos criá-la e armazená-la na variável e q :

Repare que joguei todos os termos da equação da para a esquerda, para fazer com que ela seja igual a 0 .

Passo 3

Com a equação diferencial no MATLAB, podemos usar a função l a p l a c e para calcular a transformada de Laplace dela. Lembrando que l a p l a c e tem como estrutura:

F = l a p l a c e ( f )

Ela retorna a transformada de Laplace da função f , armazenando-a na variável F .

Acrescente em seu programa o comando abaixo para calcular a transformada de Laplace de e q :

O resultado é armazenado em E . Vamos ver como ele ficou? Rode o programa que fizemos até agora e imprima E no Command Window:

Ficou uma expressão bem comprida, tive que deixar a letra minúscula para caber aqui. Mas podemos dar uma enxugada nessa expressão: note que aparecem uns termos l a p l a c e ( v _ 0 ( t ) , t , s ) em E , e eles têm exatamente a mesma estrutura da função l a p l a c e . Essa expressão representa a transformada de Laplace de v 0 ( t ) e pode ser substituída por V 0 ( s ) . No caso, chamaremos V 0 ( s ) só de V 0 .

Digite os comandos abaixo para fazer a substituição:

Primeiramente, devemos criar mais duas variáveis simbólicas: s e V 0 . Em seguida, usamos a função s u b s para pedir ao MATLAB que substitua em E a expressão l a p l a c e ( v _ 0 ( t ) , t , s ) por V 0 . O resultado da substituição é armazenado em E , atualizando a expressão anterior. Após a susbtituição, E fica assim:

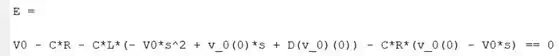
Já deu uma boa enxuagada. Agora vamos substituir as condições iniciais em E . O enunciado disse que elas são nulas, logo, v 0 0 = v ˙ 0 0 = 0 . Na expressão acima, é fácil de identificar quem é v 0 ( 0 ) . Já v ˙ 0 0 é representado por D ( v _ 0 ) ( 0 ) , um pouco mais sutil.

Para fazer as substituições, adicione ao seu programa a linha de código:

Com este comando, substituímos em E v _ 0 ( 0 ) e D ( v _ 0 ) ( 0 ) por 0 e armazenamos a nova expressão em E , no lugar da antiga. Note que usei aspas simples em ' D ( v _ 0 ) ( 0 ) ' , para indicar que os parênteses pertencem a uma expressão só. Se você tentar rodar o programa sem elas, o MATLAB acusará erro de sintaxe.

Agora E está assim:

Passo 4

Agora podemos encontrar v 0 ( t ) . Para isto, precisamos encontrar V 0 ( s ) para daí aplicar nele i l a p l a c e , para termos a inversa da tranformada de Laplace. Em E , a variável V 0 representa V 0 ( s ) e podemos usar a função s o l v e do MATLAB para encontrá-la. Adicione em seu código:

Com este comando, a função s o l v e resolve a equação E para a variável V 0 e armazena a solução em V 0 , atualizando seu valor. Na prática, isolamos V 0 na equação e V 0 passa a representar a expressão algébrica de V 0 ( s ) . Rodando o programa, temos que V 0 é igual a:

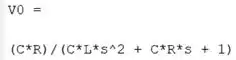
Para encontrarmos v 0 ( t ) , devemos aplicar a inversa da transformada de Laplace em V 0 ( s ) , isto é, usar a função i l a p l a c e do MATLAB em V 0 . A função i l a p l a c e tem a estrutura:

f = i l a p l a c e ( F )

Ela retorna a inversa da transformada de Laplace de F , armazenando-a na variável f .

Logo, em seu código, entre o comando:

Com este comando, o MATLAB calcula a inversa da transformada de Laplace de V 0 e armazena o resultado em v _ 0 , atualizando seu valor. v _ 0 é a solução da equação diferencial, representadno a resposta do sistema ao degrau unitário. Rodando o programa, temos que v _ 0 é igual a:

A expressão acima ficou grandinha, mas ela vai encolher quando substituirmos R , L e C pelos valores fornecidos no enunciado.

Passo 5

Vamos comparar as respostas ao degrau de um filtro de banda larga, com R = 1000   Ω , e de um filtro de banda estreita, com R = 10   Ω . O primeiro passo é substituir em v _ 0 C e L por C = 10 ∙ 10 - 5   F e L = 5 ∙ 10 - 3   H , usando o comando s u b s :

Com este comando, v _ 0 foi atualizado com valores numéricos de C e L .

Em seguida, vamos substituir R por R = 1000   Ω , para ver a resposta ao degrau do filtro de banda larga:

Armazenamos em v _ 0 _ b l a expressão de v _ 0 com R = 1000 . Vamos ver como ela ficou?

Podemos transformar as frações e as exponenciações em números decimais, usando o comando v p a do MATLAB. Este comando avalia cada elemento de uma expressão simbólica e identifica as frações ou as exponenciações com números reais, e as transforma em números “quebrados”. Por isso, acrescente no seu código o comando:

Este comando aplica a função v p a em v _ 0 _ b l e armazena o resultado em v _ 0 _ b l , substituindo a expressão anterior. Ele vai nos dar os coeficientes de v _ 0 _ b l com 7 algarismos significativos. Ao rodar programa, podemos ver v _ 0 _ b l com seus coeficientes transformados em números decimais:

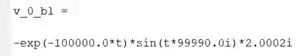
Repare que v _ 0 _ b l tem números complexos, identificados por multiplicarem i .

Vamos agora ver como é v 0 ( t ) em um filtro de banda estreita, isto é, vamos substituir R por R = 10   Ω :

Armazenamos em v _ 0 _ b e a expressão de v _ 0 com R = 10 . Rode o programa e imprima-a no Command Window para ver v _ 0 _ b e :

Bem mais simpática que v _ 0 _ b l , não?

Resposta

A resposta ao degrau do filtro de banda larga é:

v 0 B L ( t ) = - 2 i ∙ e - 10 5 t sin ⁡ ( 99990 i ∙ t )

A resposta ao degrau do filtro de banda estreita é:

v 0 B E ( t ) = 2 e - 10 3 t sin ⁡ ( 1000 t )

Exercício Resolvido #8

“Adaptado de MATLAB® for Engineering Applications, de William J. Palm III, McGraw-Hill Education, 4ª edição, 2019. Exercício 44, p. 557”

A equação diferencial que modela um certo sistema de controle de posição de uma ferramenta de corte de metal é

d 3 x d t 3 + 6 + K D d 2 x d t 2 + 11 + K P d x d t + 6 + K I x = K D d 2 x d d t 2 + K P d x d d t + K I x d

Onde a posição real da ferramenta é x , a posição desejada é x d ( t ) , e K P , K I e K D são constantes chamadas “ganhos”. Use o método da transformada de Laplace para encontrar a resposta ao degrau unitário (isto é, x d ( t ) é uma função degrau unitário). Use condições iniciais nulas. Compare a resposta para três casos:

  1. K P = 30 ,   K I = K D = 0
  2. K P = 27 ,   K I = 17,18 , K D = 0
  3. K P = 36 ,   K I = 38,1 , K D = 8,52

Passo 1

O exercício pede para encontrarmos a resposta de x ( t ) a x d ( t ) igual a um degrau unitário, usando a transformada de Laplace. Em outras palavras, precisamos encontrar a solução x ( t ) da equação diferencial de terceira ordem dada pelo enunciado. Primeiramente, aplicaremos a função l a p l a c e do MATLAB na equação diferencial para encontrarmos a transformada de x ( t ) . A transformada de Laplace de x ( t ) será indicada por X ( s ) .

Após encontrarmos X ( s ) , vamos aplicar i l a p l a c e para encontrar a inversa da transformada, isto é, x ( t ) , que é a solução da equação diferencial.

Vamos fazer esse procedimento primeiro considerando K P , K I e K D simbólicos, substituindo-os pelos valores dados pelo enunciado somente no final. Para compararmos a resposta nos três casos, substituiremos em x ( t ) os valores de K P , K I e K D e veremos como ficará a expressão simbólica para cada caso.

Passo 2

Comece entrando com a equação diferencial no MATLAB, termo a termo. Em um script novo, digite as linhas de código:

Na primeira linha, são criadas as variáveis simbólicas K p , K i , K d e x ( t ) , sendo indicado que x é em função de t .

Na segunda linha, calculamos a derivada d x d t usando a função d i f f ( x , t ) do MATLAB. Como estamos trabalhando com variáveis simbólicas, d i f f ( x , t ) apenas representa a derivada de x em relação a t e é armazenado em D x .

Na terceira linha, calculamos a derivada d 2 x d t 2 , pedindo ao MATLAB para calcular a derivada de D x em relação a t ( d i f f ( D x , t ) ). A segunda derivada de x é registrada em D 2 x .

Na quarta linha, calculamos a derivada d 3 x d t 3 , pedindo ao MATLAB para calcular a derivada de D 2 x em relação a t ( d i f f ( D 2 x , t ) ). A terceira derivada de x é registrada em D 3 x .

Na quinta linha, criamos um degrau unitário x _ d em função de t usando a função h e a v i s i d e ( t ) , representando a posição desejada da ferramenta.

Na sexta linha, definimos a primeira derivada do degrau unitário d x d d t usando d i f f ( x _ d , t ) . A derivada é armazenada em D x _ d .

Finalmenten na sétima linha, é definida a segunda derivada d 2 x d d t 2 , aplicando d i f f em D x _ d e derivando-o em relação a t ( d i f f ( D x _ d , t ) ). d 2 x d d t 2 é registrada em D 2 x _ d .

Tendo definido os termos da equação, vamos criá-la e armazená-la na variável e q , jogando todos os termos para a esquerda da igualdade e fazendo com que e q   =   0 :

Note que usei o recurso dos três pontos (...) para “quebrar” a linha de código, de forma que conseguimos ver e q inteira sem ter que usar uma barra de rolagem.

Passo 3

Tendo entrado a equação diferencial no MATLAB, vamos usar a função l a p l a c e para calcular a transformada de Laplace dela. Lembrando que l a p l a c e tem a sintaxe:

F = l a p l a c e ( f )

Ela retorna a transformada de Laplace da função f , armazenando-a na variável F .

Acrescente em seu programa o comando abaixo para calcular a transformada de Laplace de e q :

A transformada de e q é armazenada em E . Para ver como E ficou, execute o programa que fizemos até agora e imprima E no Command Window:

E ficou tão grande que quebrei ele em três prints, mas já vamos dar uma boa enxugada nele. Note que aparecem uns termos l a p l a c e ( x ( t ) , t , s ) em E , e eles têm exatamente a mesma estrutura da função l a p l a c e . Essa expressão representa a transformada de Laplace de x ( t ) e pode ser substituída por X ( s ) . No caso, chamaremos X ( s ) só de X .

Para fazer a substituição, implemente as linhas de código:

Primeiramente, criamos mais duas variáveis simbólicas: s e X . Em seguida, usamos a função s u b s para pedir ao MATLAB que substitua em E a expressão l a p l a c e ( x ( t ) , t , s ) por X . O resultado da substituição é armazenado em E , atualizando a expressão anterior. Após a susbtituição, E fica assim:

Novamente, tive que quebrar E em mais de um print, porque ainda tá enorme. Vamos fazer mais uma substituiçãozinha: o enunciado disse que as condições iniciais são nulas, isto é, x 0 = d x d t ( 0 ) = d 2 x d t 2 ( 0 ) = 0 . Na expressão acima, identificamos de cara quem é x ( 0 ) . Já d x d t ( 0 ) e d 2 x d t 2 ( 0 ) não são tão evidentes: elas são representadas por D ( x ) ( 0 ) e D ( D x ) ( 0 ) , respectivamente.

Para fazer as substituições das condições iniciais, adicione ao seu programa a linha de código:

Com este comando, substituímos em E x ( 0 ) , D ( x ) ( 0 ) e D ( D x ) ( 0 ) por 0 e armazenamos a nova expressão em E , no lugar da antiga. Note as aspas simples em ' D ( x ) ( 0 ) ' e ' D ( D x ) ( 0 ) ' , elas indicam que os múltiplos parênteses pertencem a uma expressão só, isto é, compõem uma variável simbólica. Se você tentar rodar o programa sem elas, o MATLAB acusará erro de sintaxe.

Vamos ver a nova cara de E :

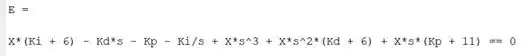
Ficou bem mais bonitinho =)

Passo 4

Com o E mais enxuto, podemos encontrar x ( t ) . Para isto, precisamos encontrar X ( s ) para daí aplicar nele i l a p l a c e , para termos a inversa da tranformada de Laplace. Em E , a variável X representa X ( s ) e podemos usar a função s o l v e do MATLAB para encontrá-la. Adicione em seu código:

Com este comando, a função s o l v e resolve a equação E para a variável X e armazena a solução em X , atualizando seu valor. Na prática, isolamos X na equação e X passa a representar a expressão algébrica de X ( s ) . Rodando o programa, temos que X é igual a:

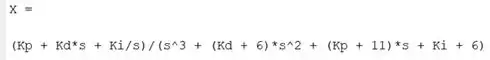
Para encontrarmos x ( t ) , devemos aplicar a inversa da transformada de Laplace em X ( s ) , isto é, usar a função i l a p l a c e do MATLAB em X . A função i l a p l a c e tem a estrutura:

f = i l a p l a c e ( F )

Ela retorna a inversa da transformada de Laplace de F , armazenando-a na variável f .

Logo, em seu código, adicione o comando:

Com este comando, o MATLAB calcula a inversa da transformada de Laplace de X e armazena o resultado em x , atualizando seu valor. x é a solução da equação diferencial, representando a resposta do sistema ao degrau unitário.

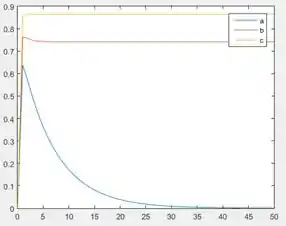
Se você rodar o programa para ver x , você vai ver que ele ficou uma expressão bem longa, com algumas comandos esquisitos (tipo r 3   i n   R o o t O f ). Vamos fazer a substituição dos ganhos K P , K I e K D para plotar curvas de x , facilitando a comparação das respostas ao degrau.

Passo 5

As opções de substituição são:

  1. K P = 30 ,   K I = K D = 0
  2. K P = 27 ,   K I = 17,18 , K D = 0
  3. K P = 36 ,   K I = 38,1 , K D = 8,52

Para implementá-las no nosso programa, usaremos a função s u b s e substituiremos as variáveis K p , K i e K d de x pelos ganhos apresentados acima:

Na primeira linha, substituímos em x as variáveis K p , K i e K d pelos ganhos da letra a e armazenamos o resultado em x _ a .

Nas linhas seguintes, fazemos a mesma coisa para os ganhos das letras b e c , registrando a substituição nas variáveis x _ b e x _ c , respectivamente.

Para plotar as curvas de x _ a , x _ b e x _ c , criamos um vetor t e m p o , indo de 0 a 50 . A ideia é substituir a variável simbólica t das expressões de x _ a , x _ b e x _ c por cada elemento de t e m p o e calcular o valor numérico de x _ a , x _ b e x _ c . Para isto, usaremos o comando s u b s para fazer a substituição de t pelo vetor t e m p o e usaremos a função d o u b l e para converter o resultado de simbólico para valores numéricos:

Por exemplo, na segunda linha acima, a variável simbólica t é substituída por cada elemento do vetor t e m p o em x _ a . O resultado dessa substituição é convertido de simbólico para numérico usando d o u b l e . O resultado da conversão é o vetor x _ a _ p l o t , que contém os valores de x _ a para cada elemento de tempo. O mesmo é feito para x _ b e x _ c .

Para gerar as curvas das respostas ao degrau, digite os dois comandos:

A função p l o t gerará o gráfico com as curvas de x _ a _ p l o t em relação a t e m p o , x _ b _ p l o t em relação a t e m p o e x _ c _ p l o t em relação a t e m p o .

O comando l e g e n d cria a legenda do gráfico, indicando que o primeiro par de vetores de p l o t representa a curva da resposta ao degrau com os ganhos de a, o segundo par, com os ganhos de b e o último par, com os ganhos de c.

Ao executar o programa, você terá as curvas de x ( t ) para cada uma das três alternativas de ganhos.

Resposta