Exercícios de Transformada de Laplace - Lista de Exercícios Resolvida

Use a transformada de Laplace para resolver o problema:

Onde é a função degrau unitário e , .

Usando o MATLAB, calcule a transformada de Laplace de .

A equação diferencial que modela o torque de um motor exigido para um certo sistema de controle de velocidade é

Onde é a velocidade desejada e é uma constante chamada “ganho”.

Use o método da transformada de Laplace para encontrar a resposta ao degrau unitário (isto é, é uma função degrau unitário). Use condições iniciais nulas.

Usando as funções e do MATLAB, encontre resolvendo a equação diferencial abaixo:

Onde é a função degrau unitário. Considere e .

A equação diferencial que modela um certo sistema de controle de posição de uma ferramenta de corte de metal é

Onde a posição real da ferramenta é , a posição desejada é , e , e são constantes chamadas “ganhos”. Use o método da transformada de Laplace para encontrar a resposta ao degrau unitário (isto é, é uma função degrau unitário). Use condições iniciais nulas. Compare a resposta para três casos:

Usando o MATLAB, calcule a inversa da transformada de Laplace de

Usando o MATLAB, calcule a transformada de Laplace de:

1. Degrau unitário ;
2. Impulso unitário .

O circuito RLC abaixo pode ser usado como um filtro de banda estreita. Se a tensão de entrada consiste na soma de tensões de variação sinusoidal com diferentes frequências, o filtro de banda estreita permitirá passar somente tensões cujas frequências estão dentro de uma faixa estreita. Esses filtros são usados em circuitos de sintonia, como os usados em rádios AM, para permitir a recepção apenas do sinal portador da estação de rádio desejada.

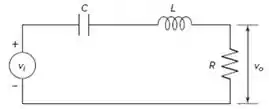
O circuito RLC tem a seguinte equação diferencial:

Onde é a tensão de saída.

Use o método da transformada de Laplace para encontrar a resposta ao degrau unitário de para condições iniciais nulas, onde e . Para modelar um filtro de banda larga, use . Já para modelar um filtro de banda estreita, use . Compare a resposta ao degrau dos dois casos.