Teoria
Quando a gente faz uma análise a gente pega uma amostra para obter informações de uma coisa muito maior, de uma população ou universo e a nossa amostra é a única fonte de informações sobre essa população!
Logo é muito muito muito importante que essa amostra represente bem o todo, certo?!
É disso que a gente vai falar hoje!!
Amostra representativa
Esse é um dos passos mais importantes de toda a análise, afinal se a amostra não for coerente com a população então os resultados não são confiáveis.
Esse problema parece bem simples quando pensamos em uma amostra de um líquido homogênio, mas a complexidade aumenta para uma mistura heterogênia e ainda mais para um sólido, como é o exemplo dos minérios.
Podemos dizer que a amostragem é dividida em três etapas:
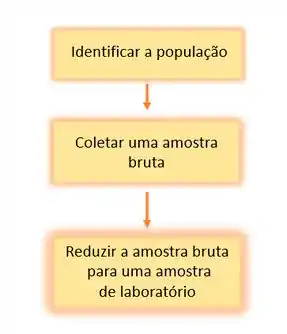
Identificar a população é a parte mais simples aqui, afinal a população é o objeto de interesse!
Chamamos de amostra bruta uma amostra composta por várias unidades de amostragem ou incrementos de amostragem, que são como mini amostras aleatórias de diferentes partes do todo.
A etapa de coletar uma amostra bruta pode ser desafiadora, dependendo do material com o qual estamos lidando!
Após essa coleta é importante adequar essa amostra para realizar as análises, de modo que a gente tenha uma pequana amostra a homogênia.
Dimensão da amostra bruta
Quanto mais incrementos de amostragem comporem a amostra bruta melhor ela vai representar a população, mas por outro lado não parece muito conveniênte ter uma amostra bruta de uma tonelada, concorda? Hahah
Então devemos tolerar um nível de incerteza e a amostra bruta deve pesar apenas o suficiente para nos dar uma resposta nesse nível de incerteza. O tamanho da amostra bruta também vai aumentar de acordo com sua heterogeneidade.
Como geralmente estamos lidando com algum nível de heterogeneidade, é mais interessante dimensionar a amostra bruta de acordo com o número de partículas .
Para uma amostra composta por partículas e , se for a probabilidade de se retirar aleatóriamente a partícula , então o desvio padrão do número de partículas do tipo retiradas é:
Podemos também escrever o desvio padrão relativo :
Mas se quisermos determinar o número de partículas para um desvio padrão escolhido, podemos fazer:
Amostragem de soluções homogênias de líquidos e gases
Em uma solução homogênia a amostra bruta pode ser bem menor que em sólidos, já que aqui a heterogeneidade esta em nível molecular e um pequeno volume de líquido tem um grande número de partículas!
Para garantir que a solução estaja homogênia a gente pode dar uma sacodida logo antes da amostragem! Mas nem sempre isso é possível, então são retiradas várias pequenas amostras que posteriormente são misturadas em um agitador!
Agora bora exercitar o que a gente terminou de aprender!!??
Dimensão da amostra bruta
Amostragem de soluções homogênias de líquidos e gases
Exercícios Resolvidos
Exercício Resolvido #1
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 8 , exercício 8-1.
Descreva as etapas envolvidas na operação de amostragem.
Passo 1
O objetivo da amostragem é obter uma amostra mais representativa possível da população ou universo. Para isso existem 3 etapas!!
Etapa 1: Identificar a população
Essa é a etapa mais direta, se queremos analizar a concentração de cloro em uma piscina, então a população é a água contida na piscina!
Etapa 2: Coletar uma amostra bruta
No exemplo da psicina se consideramos que o cloro forma uma solução com a água e portanto a concentração é uniforme em toda a piscina, então só temos que pegar um pouco da água e pronto!
Mas e se o que estivermos querendo determinar é a composição de uma amostra sólida e heterogênia?!
Nesse caso a amostra deve ser composta de um conjunto de pequenas partes tiradas de vários locais do material!
Etapa 3: Redução da amostra bruta
Nessa etapa a amostra bruta retirada da população deve ser reduzida a uma pequena quantidade de material homogênio que para ser analisado!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 8 , exercício 8-2.
Qual a função da etapa de amostragem em uma análise?
Passo 1
A etapa de amostragem é uma das etapas mais difíceis que envolve a análise e onde tem a maior fonte de erros. Isso porque a função da amostragem é garantir que a amostra é uma boa representação do todo, para obtermos um valor médio da amostra que seja uma estimativa para a média da população !
Para isso a amostra deve ser aleatória, o que não significa que a amostra seja escolhida de uma forma casual, para cada situação é importante criar um sistema para garantir essa aleatoriedade!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 8 , exercício 8-9.
Na determinação de chumbo em uma amostra de pintura, sabe-se que a variância
da amostra é de 10 ppm e a da medida é de 4 ppm. Dois esquemas de amostragem estão
sendo considerados:
Esquema a: Tome cinco incrementos da amostra e misture-os. Realize uma análise
em duplicata da amostra composta.
Esquema b: Tome três incrementos da amostra e realize uma análise em duplicata
de cada um deles.
Que esquema de amostragem, se existir algum, deve ter a menor variância em relação à média?
Passo 1
Queremos determinar qual esquema vai ter a menor variância e consequentemente vai ser o mais eficiênte.
Para isso vamos primeiro refrescar a memória e lembrar o que é variância:
A variância é inversamente proporcional a , que é o número de medidas.
Então resolvemos o problema, né? Melzinho na chupeta! No esquema A teremos duas medidas e no esquema B teremos medidas, logo o esquema B terá a menor variância, certo?!
ERRADO!!
A variância é uma medida de dispersão, ou seja mostra o quanto uma medida esta próxima da média. Então pensa comigo, em qual situação o conjunto de resultados vai ser mais preciso?
Uma duplicata realizada a partir de uma amostra homogênia ou três duplicatas de três incrementos diferentes que podem ser heterogênios?
Isso mesmo!! Os resultados a partir de uma amostra que foi misturada vão tender a ser mais próximos da média.
Portanto o esquema A deve ter menor variância com relação a média!
Resposta
Esquema A.
Exercício Resolvido #4
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 8 , exercício 8-8.
Acredita-se que aproximadamente das partículas contidas em um carregamento de
um minério de prata são de argentinita, ; o restante é silício e essencialmente não contém prata.
(a) Calcule o número de partículas que deve ser tomado para a amostra bruta se for
esperado que o desvio relativo devido à amostragem seja de 1% ou menos.
(b) Estime a massa da amostra bruta considerando que as partículas sejam esféricas
e tenham um diâmetro médio de 4,0 mm.
(c) A amostra tomada para a análise deve pesar 0,600 g e deve conter o mesmo número
de partículas que a amostra bruta. Que diâmetro devem ter as partículas para satisfazer estes critérios?
Passo 1
A gente vai tirar uma amostra bruta de um material heterogêneo, minério de prata e a primeira coisa que queremos saber é o número de partículas que devemos ter para que o desvio padrão relativo da amostragem seja de no máximo .
Para isso usamos a expressão:
Onde é o número de partículas, a probabilidade de encontramos aleatóriamente a particula de interesse e o desvio padrão relativo.
Se a particula de interesse for a argenita, o enunciado diz que do minério é composto por ela, logo a , substituindo:
Ou:
Passo 2
Mas não é muito viável ficar contando partículas, certo?! Então vamos calcular a massa dessa amostra!
Se as partículas são uniformes com ou , podemos calcular o volume da amostra:
Substituindo e calculando:
Para calcular a massa fazemos:
Mas a amostra é heterogênia, com de e de então podemos fazer:
Sabendo que e , então:
Calculando achamos:
Passo 3
Pra acabar, a gente quer saber qual é o diâmetro que as partículas devem ter para que uma massa de tenha o mesmo número de partículas que a amostra bruta!
Para isso vamos usar a expressão que usamos no passo anterior:
Substituindo a fórmula de volume:
Vamos dar uma arrumadinha:
Isolando o raio:
Mas queremos o diâmetro, então:
E ficamos com:
Substituindo os dados, lembrando que agora a massa é de :
Calculando:
Uhuuul, gostei de ver!!!!
Resposta
Exercício Resolvido #5
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 8 , exercício 8-11.
O vendedor de uma lavra de mineração tomou uma amostra do minério que pesava
5,0 kg e que tinha um diâmetro médio de partícula de 5,0 mm. Uma inspeção revelou
que cerca de 1% da amostra era de argentinita ; e o restante tinha uma densidade de cerca de e não continha prata. O potencial comprador insistiu em saber o conteúdo em prata da lavra com um erro relativo não superior a 5%. O vendedor forneceu uma amostra suficientemente grande para permitir essa avaliação?
Passo 1
Vamos ajudar o comprador descobrir se a amostra foi ou não suficiente!!
Primeiro de tudo, vamos calcular o número de partículas que uma amostra deve ter para esse desvio padrão:
Sabendo que a probabilidade de encontrar prata é de ou , temos:
Passo 2
Para achar a massa desse número de partículas, precisamos calcular seu volume:
Se o raio das partículas é , então:
Passo 3
Mas existem duas partículas com densidades diferentes, 1% de argenita e de outro material, então fazemos:
Substituindo:
Calculando:
Ou:
Mas a amostra era de , logo a amostra não é suficiente!!
Resposta
A amostra não tem tamanho suficiente.