Lei da Condutância
Teoria
A Condutância elétrica a habilidade de transportar corrente elétrica, ou seja o inverso da resistência:
Quando a gente tem um fio transportando corrente elétrica, podemos calcular essa resistência usando a lei de Ohm. Mas…e se ao invés de um fio a gente tiver uma solução?!
Condutância em uma Solução Eletrolítica
Quando uma solução contêm íons dissociados ela pode transportar corrente elétrica! Chamamos essa solução de solução eletrolítica e para medir a condutância usamos o seguinte esqueminha:
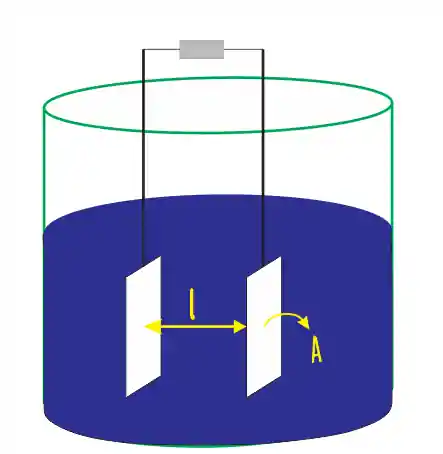
Na figura acima temos uma solução eletrolítica e um circuito fechado com dois eletrodos. A resistência desse sistema pode ser escrita como:
Onde
Podemos também definir a condutividade
📢 Clique para ver mais:
Condutividade molar
A condutividade molar é a condutância equivalente, ela corresponde a condutância de um equivalente-grama do eletrólito dissolvido em um volume que seja suficiente para preencher o espaço entre dois eletrodos separados de 1 cm. Podemos calcula-la da seguinte forma:
Onde
Lei de Kohlrausch - Migração Independente dos Íons
Lei de Kohlrausch diz que: Quando a dissociação de um eletrólito é completa, em diluição infinita, e todos os efeitos interiônicos desaparecem, cada íon migra independentemente de seu contra-íon e faz uma contribuição definida para a condutividade molar a diluição infinita do eletrólito, independente da natureza do outro íon do eletrólito.
Matematicamente podemos escrever:
A partir dessa lei podemos determinar a condutividade molar de eletrólitos fracos, a partir de valores da condutividade a diluição infinita de eletrólitos fortes.
Agora vamos praticar com exercícios?
Lei de Kohlrausch - Migração Independente dos Íons
Exercícios Resolvidos
Exercício Resolvido #1
Cadernos de Físico-Química Eletroquímica - Professora: Sonia Regina
Defina condutância, condutividade e condutância equivalente de um condutor iônico.
Passo 1
Fala aí! Vamos consolidar nossos conhecimentos com uma questãozinha teórica, beleza?
Vamos começar com o conceito de condutância, ok? Ela mede a capacidade de um solução conduzir eletricidade, ou seja, quanto maior a condutância melhor será a condução de eletricidade daquela solução.
Show! Agora vamos definir a condutividade, ela é uma propriedade usada para descrever quão bem nossa solução eletrolítica permite que os elétrons fluam por ela.
E pra fechar, vamos definir a condutância equivalente! Ela corresponde a condutância de um equivalente-grama do eletrólito dissolvido em um volume que seja suficiente para preencher o espaço entre dois eletrodos separados de … Prontinho!
Show de bola! Conseguimos!
Resposta
Passo 1.
Exercício Resolvido #2
Cadernos de Físico-Química Eletroquímica - Professora: Sonia Regina
O que diz a equação de Kohlrausch? Ela pode ser aplicada a qualquer eletrólito? Por quê?
Passo 1
Vamos dar conta de mais uma questãozinha teórica!
A lei de Kohlrausch ajuda a gente a determinar a condutividade molar de eletrólitos fracos, usando essa equação aqui:
Onde o coeficiente linear () é chamado de condutividade equivalente a diluição infinita e o coeficiente angular é a constante empírica .
Foi Kohlrausch que disse também, através da migração independente de íons, que a condutividade equivalente pode ser encontrada da seguinte forma:
Essa definição dele é válida tanto para eletrólitos fortes como para fracos, massss as condutividades molares limites dos íons só podem ser determinadas pelo estudo de eletrólitos fortes, beleza?
Arrasamos! Conseguimos!
Resposta
Passo 1.
Exercício Resolvido #3
Adaptado de Técnicas Eletroquímicas - Professor: João Batista Floriano
Determinar a solubilidade (expressar em conc. em quantidade de substância) do na água, a , sabendo que a condutividade da solução saturada deste sal é . Tendo-se usado uma água cuja condutividade é desprezível.
Dados:
Passo 1
Partiu resolver essa questão, beleza? Bom, pra isso precisamos relembrar que a relação de condutividade molar com a solubilidade é dada pela equação:
Sendo assim a solubilidade será:
Já que temos todos os dados, vamos ficar com:
Achamos a solubilidade! Conseguimos!
Resposta
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Universidade Tecnológica Federal DO Paraná - Físico-Química III
Calcule a condutividade molar limite do ácido acético e do cloreto de prata.
Dados: , , , , e .
Passo 1
Vamos fazer essa questãozinha juntos, ok?
Precisamos encontrar a condutividade molar de duas substâncias, primeiro do ácido acético () e do cloreto de prata ()... Para isso vamos usar a lei da diluição infinita de eletrólitos, beleza?
Ela diz pra gente que:
Aplicando isso aos nossos dados, vamos começar com os cálculos! Para o ácido acético vamos ter:
E para o cloreto de prata teremos:
Arrasamos! Show de bola!
Resposta
Exercício Resolvido #5
Universidade Federal do Paraná - Físico-Química
Para a , . A resistência medida para esta solução em uma dada célula foi de . Para uma solução de , a resistência medida foi de . Calcular para o .
Passo 1
Fala aí! Partiu resolver essa questão aí!
Precisamos encontrar a condutividade molar ... Para isso vamos usar a seguinte relação:
A concentração molar a gente tem, que é:
Mas ta faltando o nosso , podemos encontrar ele usando a equação:
Esse aí é a constante da célula… Vish! Não temos ele! E o é a resistência do , ela a gente tem, né?
Então, vamos encontrar a constante da célula, beleza?
Esse dados nós podemos usar do , olha só:
Sendo assim, vamos lá:
Passo 2
Agora que temos a constante da célula, a gente pode encontrar o usando a resistência do :
Agora simmmmm!! Vamos ao que nos interessa! A condutividade molar do será:
ou
Conseguimos! Uhul!