Tonoscopia, Ebulioscopia e Crioscopia
Produzido por Marcelo BrillantinoTeoria
Olar, tudo bom? 😊
Até agora já vimos váaarias coisas sobre soluções e solubilidade, mas existem algumas propriedades que ainda não vimos: as propriedades coligativas.
Propriedades coligativas são propriedades de uma solução que dependem somente da quantidade de soluto e de solvente em solução!
Ou seja, as propriedades coligativas não dependem da natureza química do soluto!
Vou repetir pra fixar na sua cabeça: a gente se interessa só na QUANTIDADE de soluto, e não em quem é esse soluto!!!!
As quatro propriedades coligativas que vamos ver são: abaixamento da pressão de vapor do solvente, aumento do ponto de ebulição do solvente, abaixamento do ponto de congelamento do solvente e a pressão osmótica 😊
Mas antes disso...
Medidas de concentração: molalidade e fração molar
Como as propriedades dependem da razão entre moléculas de soluto e de solvente, algumas unidades são bem úteis quando falamos de propriedades coligativas: a molalidade e a fração molar.
A molalidade é uma medida de concentração expressa por:
Ela é expressa por b, então também pode ser escrito:
Sua unidade mais utilizada é mol soluto/kg solvente.
Já a fração molar é a medida de proporção soluto:solvente:
Ou seja,
Abaixamento da pressão de vapor do solvente: Tonoscopia
Você lembra que a pressão de vapor de um líquido é a pressão que um gás excerce quando está em equilíbrio dinâmico com um líquido, né?
Ou seja, a pressão de vapor de um solvente é a pressão que a fase gasosa desse solvente está exercendo durante seu equilíbrio dinâmico com a fase líquida!
Um químico chamado Raoult foi ainda além, e determinou como a gente calcula essa pressão de vapor quando o líquido em questão é uma solução, e não mais uma substância pura.
A lei de Raoult diz que a pressão de vapor de um solvente é proporcional a sua fração molar em uma solução.
Onde P é a pressão de vapor do solvente em solução, a fração molar do solvente e a pressão de vapor do solvente se ele estivesse sozinho, ou seja, se a solução não fosse uma solução.
Confuso né? Vamos pegar um exemplo! Se tivermos uma solução de água com açúcar de concentração 10g açúcar/100g de água a 20oC, podemos calcular a pressão de vapor da água em solução da seguinte maneira:
Primeiro, precisamos calcular a concentração em fração molar, pra usar a lei de Raoult... Para isso, é só calcular as quantidades molares de soluto e solvente: 10g açúcar (considerando o açúcar como sacarose, de massa molar 342,3g/mol) e 100 g de água correspondem a:
Logo, a fração molar do solvente é:
Sua pressão de vapor, então, vai ser (considerando a pressão de vapor da água pura a 20oC como 17,54 Torr):
Quando comparamos a pressão de vapor da água pura (17,54 Torr) com a pressão de vapor calculada para a água em solução (17,45 Torr), percebemos que há um ligeiro abaixamento da pressão de vapor.
Podemos ampliar essa diferença para todos os solventes e todos os solutos não voláteis:
A adição de solutos não voláteis a um solvente diminui sua pressão de vapor.
Essa propriedade se chama tonoscopia.
Observação: Embora as propriedades coligativas não se “importem” com o tipo de soluto e sim com a quantidade deles, para a aplicação da lei de Raoult vamos considerar apenas solutos não voláteis, pois são os solutos que interferem na pressão de vapor...
Soluções ideais x não ideais
- Soluções ideais: são soluções que obedecem à lei de Raoult em todas as concentrações. Nessa solução as inteirações soluto-solvente são muito parecidas com as soluto-soluto e solvente-solvente.
- Soluções não ideais: são soluções que não obecem à lei de Raoult em alguma concentração de soluto.
Mas e na vida real?
As soluções reais podem ser consideradas ideais em concentrações de soluto beem baixas!
Mas relaxa que, a não ser que o exercício indique, praticamente todas as soluções são consideradas ideais.
Elevação do ponto de ebulição do solvente: Ebulioscopia
O ponto de ebulição de um líquido é a temperatura em que a pressão de vapor do líquido se iguala a pressão exterior.
Vimos que a adição de partículas não voláteis em uma solução (ou seja, o aumento da quantidade de soluto) diminui a pressão de vapor, né?
Com isso, olhando no gráfico abaixo, a curva “solução” é mais embaixo do que a curva “solvente”, que representa o solvente puro.
Para que a pressão de vapor – agora mais baixa por conta do soluto – se iguale à pressão exterior é necessário aumentar a temperatura, ou seja, um ponto de ebulição maior.
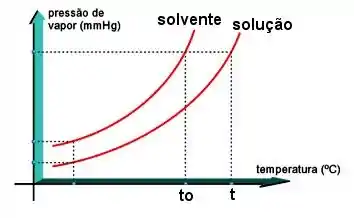
A adição de partículas de solutos não voláteis, portanto, aumenta o ponto de ebulição do solvente (propriedade que se chama ebulioscopia).
Essa propriedade de fato é pouco intuitiva, mas a gente a usa bastante na vida real.
Cozinhando macarrão, por exemplo, e colocando sal na água, estamos nos aproveitando dessa propriedade. O sal (partícula de soluto não volátil) diminui a pressão de vapor e aumenta o ponto de ebulição da água. Assim, a água pode esquentar mais antes de evaporar e mais calor é passado para o macarrão antes da água entrar em ebulição, o que acelera o tempo de cozimento.
Abaixamento do ponto de congelamento: Crioscopia
O abaixamento do ponto de congelamento é mais uma consequência do abaixamento da pressão de vapor do solvente. Assim como o ponto de ebulição muda, o ponto de congelamento também muda (e, consequentemente, o ponto triplo), como podemos ver no gráfico:
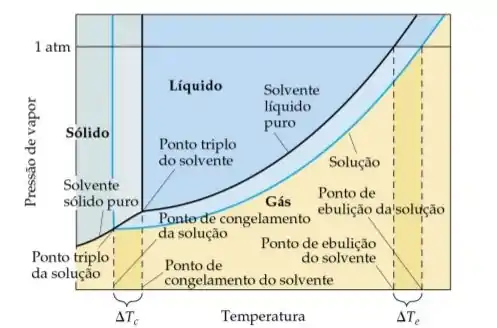
A adição de partículas de solutos não voláteis à uma solução diminui seu ponto de congelamento, e essa propriedade se chama crioscopia.
Um exemplo prático acontece nos países onde neva: para derreterem a neve que se forma nas ruas, jogam sal na neve. Esse sal funciona como o soluto não volátil na solução, e, ao diminuir o ponto de congelamento da água, faz com que a neve derreta.
E como a gente quantifica isso?
O aumento no ponto de ebulição pode ser calculado graças à proporcionalidade dessa propriedade com a molalidade da solução.
Onde é a constante do ponto de congelamento, calculada experimentalmente para cada solvente, a molalidade da solução e o fator de van’t Hoff.
O fator de van’t Hoff serve para solutos que são eletrólitos! Isso porque em soluções de eletrólitos (como ácidos, bases e sais), os íons se comportam de maneira diferente de solutos moleculares.
Por exemplo, para o HCl, que se ioniza em e , temos um fator de van’t Hoff 2, equanto pra glicose (soluto molecular), o valor é 1.
Esse fator é uma medida experimental e vamos combinar uma coisa: toda vez que o exercício não disser qual é o fator de van’t Hoff, pode considerar que é 1!
Um pouco confuso, mas se acalma que tem uns exercícios pra facilitar o rolê!
Vamos praticar?