Distribuição Normal
Produzido por Juliana EcheniqueTeoria
Imagine a seguinte situação: Estamos fazendo uma experimento químico, para isso passamos por vários passos, tiramos um volume da amostra, pesamos, tiramos a temperatura, dissolvemos, preparamos um reagente..e por ai vai!
Cada pequeno passo que a gente da pode gerar diversos erros aleatórios, um errinho somado com outro que gera um erro significativo, mas lembrando que o mesmo experimento é repetido diversas vezes, qual é a probabilidade de todos os erros aconteceram ao mesmo tempo?!
É exatamente esse o espirito da coisa na distribuição normal!
Curva de distribuição padrão
Se um experimento, repetido várias vezes tiver apenas erros aleatórios, então os resultados tendem a se agrupar em torno de um valor médio!
Seguindo esse raciocínio a gente tem a curva de distribuição normal ou curva gaussiana:
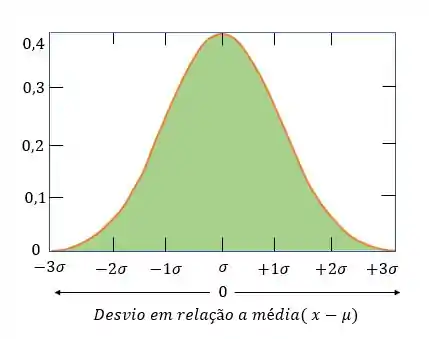
A curva de distribuição normal é muito utilizada para modelar fenômenos naturais. Mas ai você me pergunta: “ o que fenômenos naturais tem a ver com análise de dados em um experimento químico?!”
Mas o que são fenômenos naturais se não eventos aleatórios!!
Segundo a curva de distribuição normal dos dados estão entre e desvio-padrão, entre e entre . A equação da curva é dada pela seguinte expressão:
Parâmetros
Na curva de distribuição normal encontramos os parâmetros que queremos estimar nas análises estatísticas, a média da população e o desvio-padrão da população , que são fornecidos pelas seguintes equações:
Diferente da média da amostra , aqui é o número total de medidas de toda a população.
O desvio-padrão da população é dado por:
Histograma
Uma forma de trazer a curva gaussiana um pouco mais pra realidade da estatística é fazendo um histograma. Por exemplo, ao analisar a concentração de óleo no mar por causa de um derramamento de óleo, poderiamos ter um histograma da seguinte forma:
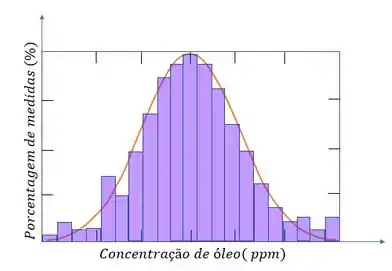
Os dados obtidos foram organizados em faixas de ordem crescente e o eixo mostra a porcentagem em que cada faixa aparece. A ideia é que quanto mais dados a gente tem mas o histograma fica com o formato parecido com a curva de distribuição normal!
A medida que então !!
Os parâmetros são determinados pelas medidas da amostra, o desvio-padrão da amostra pode ser dado por:
Ou:
E o quadrado do desvião-padrão da amostra é sua varância, que nada mais é do que outra forma de determinar precisão:
Agora bora exercitar o que a gente aprendeu!!!