Introdução a Métodos Estatísticos
Produzido por Juliana EcheniqueTeoria
Imagina que houve um derramamento de petróleo no mar e você é o responsável por fazer testes que vão determinar sua proporção!
Não tem como analisar TODA água do mar, certo?!
Então você vai pegar parcela da água do mar em diversos raios para analisar e determinar a concentração de óleo!
Os métodos estatísticos ajudam a gente tratar os dados para que eles reproduzam com o máximo de fidelidade a realidade!
Mas primeiro vamos a alugumas definições..
- População
- Amostra
- Média
- Mediana
- Precisão
- Exatidão
A população, ou universo é o nosso objeto de interesse, no nosso exemplo a população é um raio dentro do mar, a partir do local onde o acidente aconteceu!
De uma forma geral, podemos dizer que a população é o conjunto de todos os ítens ou indivíduos que tem pelo menos uma característica em comum a ser analisada, onde estão todas as medidas de interesse!
Muitas vezes a população é conceitual, impossível de se analisar, como é o caso do exemplo de derramamento de petróleo! Em outros momentos é só muito burocrático estudar toda a população, e é ai que entra a estatística!
Ao invés de realizar medidas em toda a população, elas são realizadas em um subconjunto da população cuidadosamente selecionada, chamada de amostra!
Para a gente entender a relação população x amostra a gente pode dar uma olhadinha nesse diagrama:
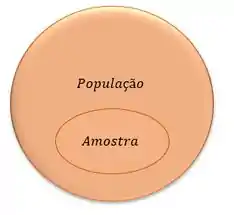
Aqui é legal a gente ficar atento na diferença de amostra estatística para amostra analítica, essa amostra que a gente esta definindo é a amostra estatística, enquanto a amostra estatística resulta em um conjunto de medidas a amostra analítica representa apenas uma medida.
Como vários testes são feitos não é interessante estudar cada um individualmente, certo?! Podemos então calcular a média aritmétrica dos resultados, :
Onde é cada medida e é o número de réplicas.
A mediana é um valor central de um conjunto. Por exemplo, análises foram feitas na água do mar contaminada com óleo e foram obtdos os seguines resultados em partes por milhão, ppm:
Pra a gente descobrir a mediana, primeiro organizamos esses valores em ordem crescente e depois identificamos o valor central:
Nesse caso a mediana é . Mas e se não tiver um valor central? E se o número de medidas for par?!
Vamos supor que ao invés de medidas tenhamos :
Nesse caso temos dois valores centrais e para descobrir a mediana, calculamos sua média:
Achamos a mediana igual a !!!
A precisão esta relacionada ao quão bem uma medida é reproduzida! Em um conjunto de medidas precisa os seus valores numéricos estão próximos entre si.
Vamos imaginar as medidas como um tiro ao alvo! Cada pontinho vermelho é uma medida:
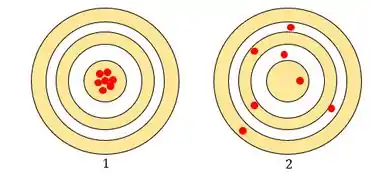
No primeiro alvo, os tiros são precisos, diferente do segundo que cada pontinho ta distante um do outro!
Uma forma de mensurar precisão é o desvio em relação a média:
Onde é a diferença da média e o valor real!
Se todas as medidas possuem um valor próximo entre sí, dizemos que a medida é precisa mas e se o instrumento estiver mal calibrado?! Então mesmo que as medidas sejam próximas, elas não vão representar bem a realidade, certo?!
É ai que entra a exatidão!!!
A exatidão é o quanto uma medida esta próxima da realidade! Voltando ao exemplo do tiro ao alvo, vamos adicionar mais duas situações:
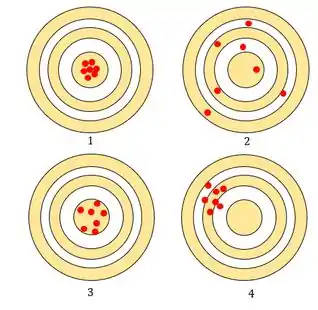
O objetivo é atirar no centro, então vamos dizer que os tiros são exatos quando eles estão o mais próximo do centro!
Nesse caso os tiros do primeiro alvo são precisos e exatos e do segundo não são nem precisos nem exatos. Agora no terceiro, todos os tiros estão no centro, eles são exatos e relativamente precisos também, porém menos do que no primeiro!
E por último a gente tem vários tiros juntinhos, logo eles são precisos, mas como estão longe do centro, não podemos dizer que eles são exatos. Esse é o caso de medidas realizadas a partir de um instrumento mal calibrado!
A exatidão de um resultado é expressa pelo erro, o erro absoluto, , é a diferença entre o valor verdadeiro e o valor medido:
Aqui é o valor verdadeiro.
Uma forma mais interessante é calcular o erro relativo que da pra a gente o percentual do erro:
Mas agora eu te pergunto, se o que queremos na análise é justamente achar o valor verdadeiro, como a gente vai calcular o erro?!
Estimar o erro é um grande desafio nas análises e é por isso que temos que entender quais são os tipos de erros, como evita-los e como conviver com os que a gente não consegue evitar!
Tipos de Erros
Os erros podem ser sistemáticos ou aleatórios e tratamos cada tipo de erro de uma maneira diferente!
Os erros sistemáticos também são chamados de erros determinados, conhecemos sua causa e apesar deles serem impossíveis de eliminar, podem ser reduzidos e calculados! Por exemplo se tirarmos alíquotas de da amostra de água do mar com uma pipeta mal calibrada teremos várias medidas com volumes parecidos, porém distantes do valor real.
Em outras palavras as medidas vão ser precisas mas não exatas.
Já os erros aleatórios, é a verdadeira pedra no nosso sapato! Conhecemos ele como erros indeterminados, esses erros existem em todas as medidas, são provocados por inúmeras varáveis que não podemos controlar e muitas vezes nem a fonte do erro pode ser identificada!
Quanto maior o número de medidas, mais o valor da média vai se aproximar do valor real, e as medidas vão se distribuir aleatoriamente ao redor do valor verdadeiro.
Sendo assim, termos medidas extas porém pouco precisas!
Agora partiu exercitar!!??