Limites de Confiança
Produzido por Juliana EcheniqueTeoria
Imagina que queremos determinar a dureza da água de uma fonte, para isso a gente determina a concentração dos íons de determinados minerais, principalmente e , vários testes são realizados e isso da para a gente alguns resultados que variam um pouco entre si.
Ai eu te pergunto, qual o resultado que corresponde a realidade?!
A verdade é que a gente não consegue ter de certeza de um resultado, por ao invés de ir atrás de um resultado verdadeiro, é mais interessante falar de um intervalo que é uma faixa de valores em torno da média da amostra onde existe uma probabilidade da média da população estar.
Esse intervalo é chamado intervalo de confiança, IC e o menor valor e o maior valor ao redor da média são chamados limites de confiança!
Dizemos que a probabilidade do parâmetro estar entre oss limite inferior, superior é de e esse é o nosso nível de confiança, NC.
Lembrando que o parâmetro é o valor real que queremos estimar, nesse caso é a média da população .
Por exemplo, se dizemos que é 90% provável que a concentração de cálcio na água esteja em um intervalo de , então o NC é de , é o IC, o é e o é !
IC quando é uma boa estimativa de
A amplitude do IC pode ser calculado a partir do desvio padrão da população , o problema é que dificilmente vai ser possível conhecer esse valor, porque é impossível analisar TODA a água da fonte, por exemplo.
Mas quando realizamos muitos testes podemos dizer que o desvio padrão da amostra é uma boa estimativa para o parâmetro !
Nesse caso IC é dado por:
Onde é o número de amostras e é uma nova variável, definida como:
Dessa forma quando a diferença entre uma medida e a média é de um desvio padrão () então , quando essa diferença é , e assim sucessivamente! diz pra gente o desvio que um dado tem da média de uma forma relativa.
Quanto maior a amplitude do IC maior é a probabilidade de estar dentro do intervalo de confiança, mas na prática a gente quer um IC pequeno para o maior NC possível!
Para uma distribuição normal, temos:
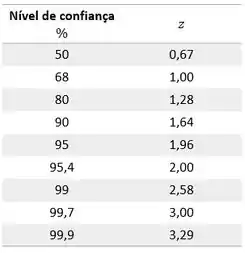
que pode ser escrito como:
Dessa forma:
E:
De uma forma geral, podemos dizer que :
IC quando não pode ser estimado
Aprendemos a calcular o IC quando pode ser estimado por , o problema é que muitas análises químicas, por limitação de tempo ou recursos, são feitas em duplicatas ou triplicatas! Isso é, repetidas duas ou três vezes.
Como discutimos, só é uma boa estimativa de quando estamos trabalhando com muitas medidas!
Nesse caso pode ser interessante usar intervalos de confiança maiores e a variabilidade de pode ser dado por:
Esse parâmetro é bem parecido com o , a única diferença é que substituimos por ! Para medidas podemos escrever:
Nesse caso, para calcular o intervalo de confiança, usamos:
Podemos obter consultando essa tabelinha aqui:

Onde o grau de liberdade é dado por .
Agora bora exercitar!!!
IC quando s é uma boa estimativa de σ
IC quando σ não pode ser estimado
Exercícios Resolvidos
Exercício Resolvido #1
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 7 , exercício 7-2.
Considerando um grande número de medidas de forma que s seja uma boa estimativa de , determine que nível de confiança foi usado para cada um dos intervalos de confiança:
Passo 1
Opaa, temos então várias expressões para intervalos de confiança!
Só pra refrescar a memória, vamos ver a expressão geral, o problema diz que é uma boa estimativa de , então podemos considerar:
E como a gente pode saber o nível de confiança?!
Muito simples, a gente vai consultar essa tabelinha aqui:
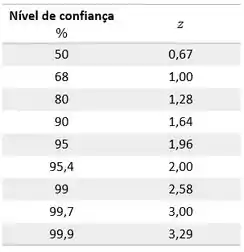
E como podemos ver, o é o número que esta multiplicando o em cada letra! Então vamos começar com a letra
Consultando a tabela achamos que para o nível de confiança é de !
Passo 2
Agora vamos fazer a mesma coisa para as outras letras!
Na letra temos , consultando a tabela ;
Para , essa é a nossa letra ;
E pra acabar, para , ;
Molezinha, não é!?
Resposta
Exercício Resolvido #2
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 7 , exercício 7-3.
Discuta como a dimensão do intervalo de confiança da média é influenciada pelos
seguintes aspectos (todos os outros fatores são constantes):
- O tamanho N da amostra.
- O nível de confiança.
- O desvio padrão s
Passo 1
Vamos ver se a gente aprendeu direitinho sobre os conceitos de Limites de confiança!!!
A medida que o número de medidas aumenta, então a média das amostras, se aproxima mais da média da população .
E o que isso tem a ver com o intervalo de confiança?!
Tudo! Isso significa que o resultado é mais confiável, assim o intervalo de confiança pode ser menor!
Matemáticamente temos:
Aqui vemos que o intervalo de confiança é inversamente proporcional ao número de amostras. aumenta e diminui, como discutimos!!!
Passo 2
O nível de confiança é nada mais nada menos do que a probabilidade de estar dentro do intervalo de confiança estabelecido, certo?!!
Concorda comigo então que se eu aumento o intervalo de confiança essa probabilidade aumenta?!
Isso mesmo, a medida que aumenta, o aumenta também!
Passo 3
A relação entre e a gente também pode ver matemáticamente:
que nada mais é do que o desvio padrão da população estimado por é diretamente proporcional a .
Se a gente parar pra pensar faz bastante sentido, porque o aumento de significa que as medidas não são muito precisas, logo a gente tem que aumentar o intervalo onde provavelmente vai estar!
Resposta
- diminuiu com o aumento de na proporção de ;
- aumenta com o aumento do ;
- aumenta na mesma proporção que o aumento de .
Exercício Resolvido #3
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 12 , exercício 12-9.
Os níveis de glicose de um paciente que sofre de diabetes foi monitorado durante um mês por meio de um método analítico espectrofotométrico e os seguintes dados foram obtidos:

Determine os intervalos de confiança de 80% e 95% para (a) o primeiro registro (b) o valor médio, considerando uma boa estimativa para .
Passo 1
O problema diz pra a gente que é uma boa estimativa para , logo podemos usar a seguinte expressão:
Podemos consultar a tabelinha da teoria que relaciona o nível de confiança com e vemos que para um e para , substituindo:
Calculando:
E:
Ficamos com:
Passo 2
Agora para o valor médio, :
Esse é o limite de confiança que a gente calculou no passo , então podemos usar ele:
Calculando:
Agora para de confiança:
Ficamos com:
Awee, muito bem!!!
Resposta
- , ;
- , .
Exercício Resolvido #4
Lista poli-USP.
Se uma amostra aleatória , tem uma média amostral de e uma desvio padrão populacional de . Construa o intervalo com de confiança para a média populacional .
Passo 1
Queremos construir um intervalo de confiança que tenho um nível de confiança de .
O problema nos da o número de medidas, , e o pode ser calculado por:
Sabendo que para , , então:
Calculando:
Outra forma de escrever é:
Resposta
Exercício Resolvido #5
Lista poli-USP
Uma marca particular de margarina diet foi analisada para determinar o nível em porcentagem de ácidos graxos insaturados. Uma amostra de seis pacotes resultou nos seguintes dados: 16,8; 17,2; 17,4; 16,9; 16,5 e 17,1. Encontre o intervalo de confiança de 99% para a amostra
Passo 1
Queremos achar para um , mas o problema não so disse se é uma boa estimativa de , logo vamos assumir que não é!
Assim vamos usar:
Sabemos que o número de medidas é 6 e precisamos então calcular , e determinar !
Passo 2
Vamos começar calculando a média :
Agora o desvio padrão, :
Calculando:
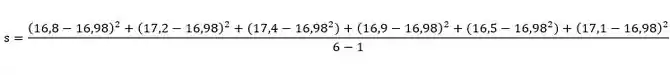
Achamos .
para um nível de confiança de com graus de liberdade é !
Passo 3
Agora podemos achar nosso intervalo de confiança:
Calculando achamos:
Ou também podemos escrever: