Fórmulas Químicas
Produzido por Juliana EcheniqueTeoria
Fala aí! Seja muito bem vindo ao RespondeAí! Bora aprender as diferentes Fórmulas Químicas!
Existem várias formas de representar uma molécula, algumas dão mais informações sobre o composto, enquanto outras dão menos, mas cada uma é útil no seu momento!
Então sem mistério, se liga nessa imagem com todas as fórmulas químicas que você precisa saber!
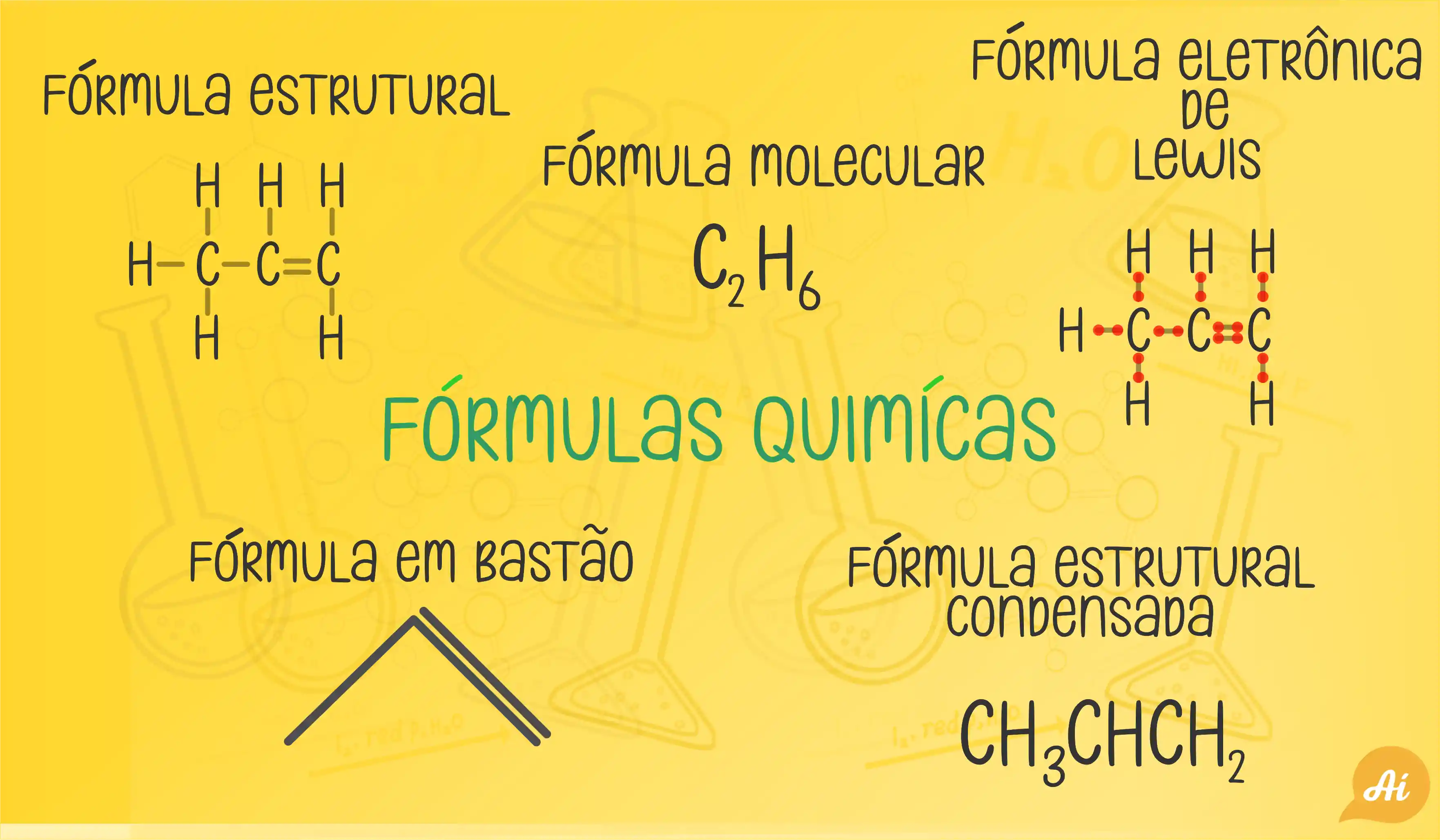
Pra entender melhor cada fórmula química você pode conferir esse vídeo aqui em baixo! 👇
Ou então segue comigo pra um resuminho em texto! 😉
Fórmula Molecular
É a maneira mais simples de representar uma molécula. Ela informa quais átomos estão presentes na molécula e suas respectivas quantidades.
Por exemplo:
Que é a fórmula molecular da glicose! Ela nos diz que essa molécula tem então 6 átomos de carbono (C), 12 átomos de hidrogênio (H) e 6 átomos de oxigênio (O).
Agora você me pergunta, eu posso colocar os átomos em qualquer ordem? Por que que o carbono vem primeiro?
Então, tem uma ordem certa sim! E isso ai é tudo convenção que a galera da antiga escolheu. Se liga nessa dica maneira que eu vou dar!
Quando você quiser escrever a fórmula molecular de um substância, lembra da palavra MACHO, e vai na ordem:
- Metais
- Ametais
- Carbono
- Hidrogênio
- Oxigênio
Fórmula Estrutural
Essa aqui é a fórmula estrutural do propano, que tem como fórmula molecular
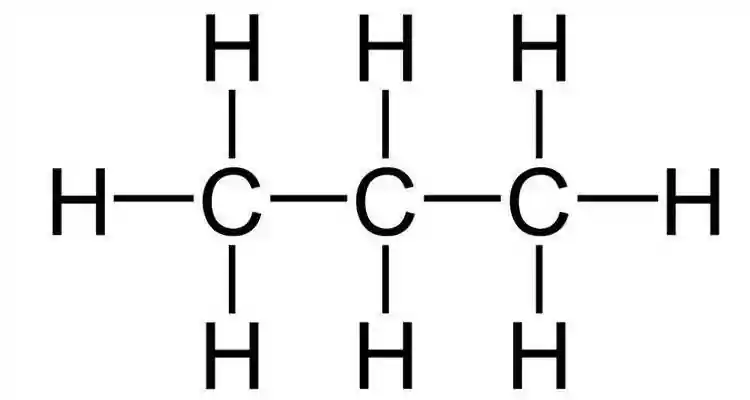
Fórmula Estrutural Condensada
Essa fórmula é como se fosse uma mistura da fórmula estrutural e a fórmula molecular. Se quisermos colocar a molécula do exemplo anterior, propano na fórmula estrutural condensada ele vai ficar com essa carinha aqui:
Fórmula em Bastão
É a fórmula mais usada, também conhecida como fórmula condensada linear! Essa estrutura mostra a estrutura e ligações das moléculas, omitindo os átomos de carbono, de forma que a estrutura fique simplificada
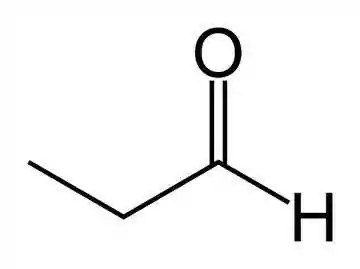
Essa é a estrutura do propanal! É um aldeído que tem 3 átomos de carbono e uma dupla ligação com o oxigênio no carbono da ponta.
Os carbonos e os hidrogênios ligados a eles ficam omitidos! A estrutura dele na fórmula estrutural é essa aqui:
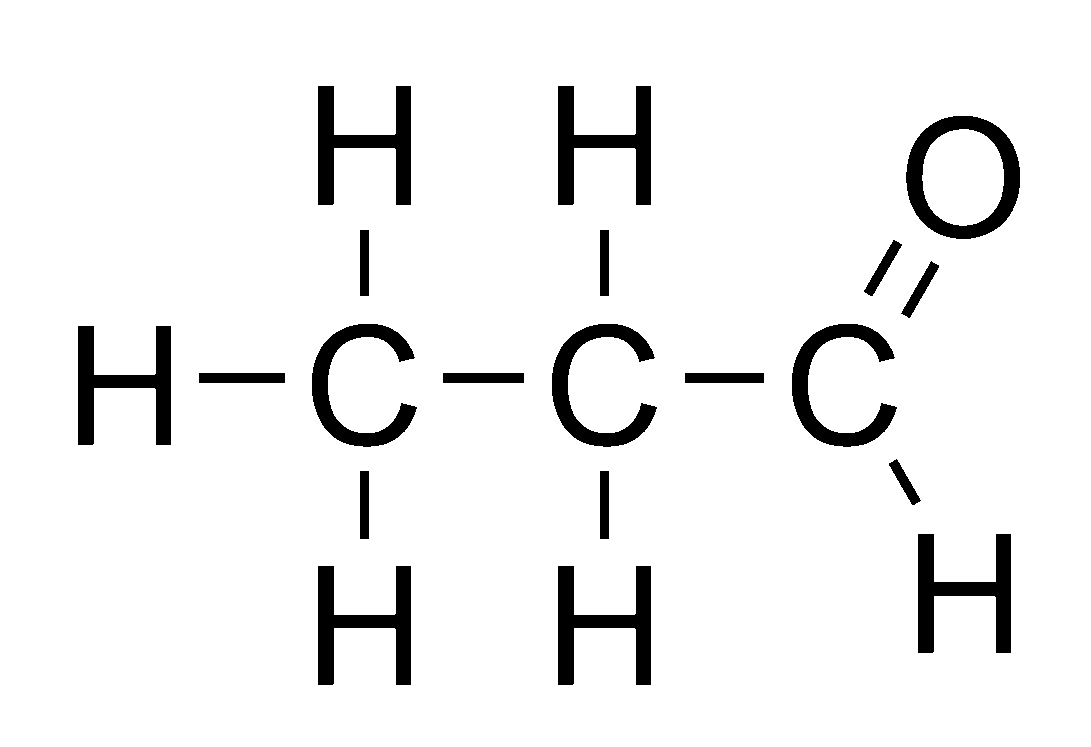
Fórmula Eletrônica de Lewis
Essa forma de representação é menos usada, mas ela é interessante, porque nesse tipo de estrutura os elétrons da camada de valência são representados por bolinhas!
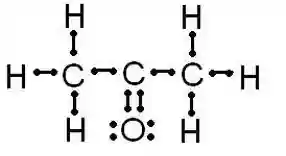
Essa fórmula mostra a quantidade e a posição dos elétrons que estão na última camada eletrônica do átomo. As ligações existentes são representadas por esses traços que ligam um elétron ao outro, e no caso de ligações dativas, elas são representadas por setas.
Resumo:
- A fórmula molecular nos diz quais e quantos átomos de cada elemento estão presentes em uma molécula de um composto.
- A fórmula estrutural nos mostra a estrutura e as ligações entre os átomos.
- A fórmula condensada nos mostra cada fragmento da estrutura como uma fórmula molecular parcial.
- A fórmula em bastão ou condensada linear nos mostra a estrutura e as ligações, omitindo os carbonos e os hidrogênios.
- Por último, a fórmula eletrônica de Lewis mostra a estrutura, as ligações e os elétrons da camada de valência de cada átomo.
A maioria dos exercícios envolvendo fórmulas químicas pedem pra você converter uma na outra. Então você vai precisar saber as informações que cada fórmula dá e usar um pouquinho de matemática para convertê-las.
Agora bora praticar com exercícios?!
Fórmula Molecular
Fórmula Estrutural
Fórmula Estrutural Condensada
Fórmula em Bastão
Fórmula Eletrônica de Lewis
Resumo:
Exercícios Resolvidos
Exercício Resolvido #1
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp F49-F.4.
A espectrometria de massas dá para a vitamina C a massa molar . Sabendo que a fórmula empírica é , qual é a fórmula molecular da vitamina C?
Passo 1
Aqui o objetivo é passar da fórmula mínima para a fórmula molecular.
E como fazemos isso?
Vamos calcular a “massa molar” do composto caso sua fórmula molecular fosse igual a sua fórmula mínima.
Depois, vamos dividir a massa molar real pela massa molar da fórmula mínima. Assim, vamos ver quantas vezes a fórmula mínima precisa ser multiplicada para “atingir” a fórmula molecular.
Partiu?
Passo 2
Massa molar da fórmula unitária:
Passo 3
Dividindo a massa molar da vitamina C (fornecida pelo enunciado) pela massa molar da fórmula mínima, encontramos:
Portanto, na fórmula molecular da vitamina C, multiplicamos os índices da fórmula mínima pelo fator :
Resposta
Exercício Resolvido #2
UFRJ – Química Geral I (Estequiometria, teoria atômica e periódica). Prof. Emerson. Questão 02.
Dê a fórmula mínima de cada um dos seguintes compostos, se uma amostra contém:
a) mol de , mol de e mol de ;
b) g de ferro e g de oxigênio.
Passo 1
a) A fórmula mínima deverá mostrar a proporção entre () através de números inteiros.
Analisando o número de mols de cada elemento, percebemos que é a metade de , que é um terço de .
Portanto, se representarmos a quantidade de oxigênio ( mol) por , a quantidade de carbono () deverá ser 2, para que seja o dobro. E a quantidade de H, para que seja o triplo da quantidade de carbono, deverá ser 6.
A fórmula mínima é, então, dada por:
Passo 2
b) No item b, vamos transformar as massas fornecidas em número de mol através da massa molar dos elementos. E analisaremos as proporções entre os números de mols para determinar a fórmula mínima.
Olha aí a massa molar do ferro e do oxigênio:
E as massas de e , dadas no enunciado:
Portanto, o número de mols de cada um pode ser calculado por:
E a fórmula mínima poderia ser assim:
Só que não.
Porque a gente precisa de números inteiros como índices, certo?
Mantendo as proporções, a fórmula mínima do composto será:
Resposta
a)
b)
Exercício Resolvido #3
UFS – Lista de Físico-Química. Prof. Dr. Juvenal Filho. Questão 05.
Sabendo que a fórmula mínima do benzeno é e que a sua massa molar é de , determine a fórmula molar do benzeno.
Passo 1
Mais uma vez vamos calcular a “massa molar” da fórmula mínima e ver quantas vezes ela precisa ser repetida para atingir a massa molar do benzeno.
O fator que multiplica a massa molar da fórmula mínima para atingir a massa molar será o mesmo que multiplicará os índices na fórmula mínima para atingir a fórmula molecular (que foi chamada de fórmula molar).
Passo 2
A massa molar da fórmula mínima será dada por:
A razão entre a massa molar do benzeno e de sua fórmula mínima é, então:
Como precisamos de um número inteiro, vamos considerar que o fator seja 6.
Passo 3
A fórmula molecular do benzeno será, então:
Resposta
Exercício Resolvido #4
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp F46-Teste F.1A. Modificado.
Há séculos, os aborígenes australianos usam folhas de eucalipto para aliviar gargantas irritadas e outras dores. O ingrediente ativo primário foi identificado e recebeu o nome de eucaliptol. A análise de uma amostra de eucaliptol de massa total g mostrou em sua composição g de carbono, g de hidrogênio e g de oxigênio. Determine as percentagens em massa de carbono, hidrogênio e oxigênio no eucaliptol. Determine ainda sua fórmula molecular, sabendo a massa molar do composto é igual a g/mol.
Passo 1
Pro cálculo de composição percentual a gente só vai dividir a massa de cada um dos elementos pela massa total da amostra.
Quem prefere calcular porcentagem por regra de três, fica a vontade viu. Somos de exatas e sabemos que a matemática nos permite calcular por caminhos diversos chegando ao mesmo resultado.
Passo 2
Pra determinar a fórmula molecular, precisamos determinar a fórmula mínima primeiro.
Para isso, vamos calcular o número de mols de cada um dos elementos na amostra mencionada pelo enunciado.
Na tabela periódica vemos que:
E o número de mols dessa galera pode ser calculado por:
Vamos considerar que a fórmula mínima contem 1 oxigênio.
Como a proporção entre e é dada por , a fórmula mínima terá 10 carbonos.
Sendo a proporção entre H e C dada por , a fórmula mínima terá 18 hidrogênios.
Passo 3
Por último, precisamos transformar a fórmula mínima em fórmula molecular.
Para isso vamos calculr a massa molar da fórmula mínima, dividir a massa molar por essa massa que calculamos e determinar qual o fator que multiplicando a fórmula mínima nos leva à fórmula molecular.
A massa molar da fórmula mínima será:
Dividindo a massa molar do eucaliptol (fornecida pelo enunciado) pela massa molar da fórmula mínima, encontramos:
Portanto, na fórmula molecular coincide com a fórmula mínima.
Resposta
Fórmula molecular:
Exercício Resolvido #5
Unicamp – Química Geral e Inorgânica. Prof. Nelson. P1-2015.1. Questão 01.
Uma amostra de (monóxido de dinitrogênio) contendo 4,33 g é composta de 63,65% de nitrogênio () e 36,35% de oxigênio (), em massa. Qual a composição percentual de uma amostra de 14,9 g de ?
Passo 1
Isso aí tá ate parecendo pegadinha.
Mas olha só... A porcentagem em massa (composição percentual) de uma amostra é uma propriedade intensiva, ou seja, independe da quantidade de massa analisada.
Portanto, se você pegar 1 g de uma amostra ou 100 g da mesma amostra, a composição percentual delas será a mesma!
Passo 2
Se 4,33 g de uma amostra de tem composição percentual igual a 63,65% de nitrogênio e 36,35% de oxigênio , a composição percentual de uma amostra de 14,9 g do mesmo composto será igual: 63,65% de nitrogênio e 36,35% de oxigênio.
Aliás, qualquer amostra de puro terá essa composição. Olha só:
Em 1 mol de ( g), a gente tem 2 mols de ( g) e 1 mol de ( g).
Portanto, a composição percentual será dada por:
Resposta
63,65% de nitrogênio e 36,35% de oxigênio.
Exercício Resolvido #6
USP – Lista de Exercícios de Estequiometria. Questão 05.
O cobre forma dois óxidos. Em um deles, existem g de oxigênio combinado com g de cobre. No outro, existem g de oxigênio combinados com g de cobre. Demonstre que estes dados ilustram a lei das proporções múltiplas.
Passo 1
Primeiramente, o que é essa tal lei das proporções constantes?
Essa lei foi enunciada por Dalton. Aquele do modelo atômico bola de bilhar.
Como Dalton ficava lá dizendo que o átomo era indivisível, ele acreditava que, ao formar compostos, os átomos se combinavam através de números inteiros.
Ou seja: era impossível você ter 1 átomo de hidrogênio se combinando com átomos de oxigênio. Se esses caras se combinavam na razão de 2:1, então 2 átomos de hidrogênio deveriam se combinar com 1 átomo de oxigênio.
Embora o modelo atômico de Dalton tenha caído em desuso, a Lei das Proporções Múltiplas é válida!
Ela diz que os átomos se combinam através de números inteiros e que, caso dois elementos sejam capazes de se combinar formando mais de um composto (tipo , , ...), caso a gente fixe a massa de um dos elementos em todos os compostos, as massas do outro elemento nos diferentes compostos terão entre si uma razão inteira.
Entre e , por exemplo, fixando a massa de oxigênio com g, temos g e g de nitrogênio, respectivamente. E a razão entre e é um número inteiro: .
Passo 2
O papo tá bom (mentira), mas vamos para o que interessa.
No primeiro óxido entre Cu e O, o número de mols de Cu é dado por:
E o número de mols de O:
Como o número de mols de Cu é o dobro do de O, a fórmula mínima desse óxido seria .
E no segundo óxido:
Como o número de mols de Cu e O são iguais, a fórmula mínima do óxido será .
E os átomos então combinado através de números inteiros, mas isso meio que a gente “faz acontecer” né.
Passo 3
Mas a Lei das Proporções Múltiplas diz que fixando a massa de um dos elementos, as massas do outro elemento terão entre si uma razão inteira.
O enunciado já fixa a massa de Cu em 10 g, só precisamos ver se, de fato, a razão entre as massas de oxigênio dos dois óxidos é um número inteiro:
Beleza! Os óxidos de cobre expostos estão ilustrando a lei das proporções múltiplas.
Resposta
Exercício Resolvido #7
UFS – Lista de Físico-Química. Prof. Dr. Juvenal Filho. Questão 02.
Qual a fórmula molecular de cada um dos compostos?
a) Fórmula mínima , massa molar g/mol
b) Fórmula mínima , massa molar g/mol
c) Fórmula mínima , massa molar g/mol
Passo 1
Faremos a mesma coisa nos três itens:
Primeiro calculamos a massa molar da fórmula mínima.
Depois calculamos a razão entre a massa molar do composto e da fórmula mínima.
Por último, utilizamos o fator calculado acima para multiplicar a fórmula mínima, encontrando a fórmula molecular.
Passo 2
a)
Fórmula molecular será a fórmula mínima com os índices multiplicados pelo fator 6:
Passo 3
b)
E a fórmula mínima coincide com a fórmula molecular!
Passo 4
c)
E a fórmula molecular será a fórmula mínima com os índices multiplicados pelo fator 2:
Resposta
Exercício Resolvido #8
UFRJ/IQ – Química Geral. Prof. Luiz Fernando Malta. P3. Questão 03.
A combustão de 11,5 g de etanol forneceu 22,0 g de e 13,5 g de . Determine a sua fórmula mínima.
Passo 1
A combustão envolve a reação de um composto com oxigênio (é uma oxidação). Caso a combustão seja completa, os produtos serão e água ().
Então a combustão do etanol será algo como (não balanceada):
Vamos fingir que a gente não tem a menor idéia de como é o composto etanol, ok?
Observe que, como temos carbono e hidrogênio nos produtos, o etanol precisar ter esses elementos na sua fórmula química. Além disso, ele pode ou não ter oxigênio.
Passo 2
Como foi dada a massa de e O formada, e podemos descobrir a massa de consumida (por diferença entre a massa de produtos e reagentes), assim como a massa molar dessa galera, vamos descobrir o número de mols envolvidos na reação.
O que faz com que a nossa equação química “semi-balanceada” fique igual a:
Trabalhando com número inteiros:
Como temos 2 carbonos do lado direito da equação, precisamos ter 2 carbonos no lado esquerdo:
Contando os hidrogênios e os oxigênios:
E a fórmula mínima do etanol foi encontrada!
Perceba que todos os índices são inteiros e não podemos reduzir a fórmula ainda mais porque temos um índice igual a 1!
Resposta
Exercício Resolvido #9
UFRJ – Química Geral I (Estequiometria, teoria atômica e periódica). Prof. Emerson. Questão 5. Modificada.
O glutamato monossódico (GMS) é suspeito de ser o responsável pela “síndrome do restaurante chinês”. Nos indivíduos sensíveis, os sintomas começam 20 minutos após a ingestão do glutamato monossódico. O GMS tem a seguinte composição em massa: 35,51% C, 4,80% H, 37,82% O e 8,29% N e 13,60% Na.
Qual a fórmula molecular desse composto, sabendo que a sua massa molar é cerca de 170 g?
Passo 1
Para transformar a composição percentual em fórmula molecular, começamos “fingindo” que temos uma amostra de 100 g do composto. Neste caso, teremos 35,51 g de C, 4,80 g de H, 37,82 g de O, 8,29 g de N e 13,60 g de Na.
Com essas massas e as massas molares dos elementos, vamos calcular o número de mols de cada elemento na fórmula mínima. Confere a massa dos elementos na tabela periódica.
A nossa fórmula mínima deve obedecer, portanto, a seguinte proporção:
Mas só podemos usar números inteiros.
Uma boa estratégia para fazer isso é igualar o menor a 1. Nesse caso estaremos usando um fator de multiplicação igual a , que deverá ser aplicado a todos os compostos:
Fórmula mínima encontrada!
Para transformar a fórmula mínima em fórmula molecular, vamos usar a massa molar do composto.
Passo 2
O enunciado já diz que:
E a massa molar da fórmula mínima é dada por:
Para a determinação da fórmula molecular, dividimos a massa molar pela massa molar da fórmula mínima, obtendo:
Como precisamos de um valor inteiro, utilizamos a aproximação .
Portanto, a fórmula molecular será idêntica à fórmula mínima.
Já podíamos desconfiar, considerando que o nome do composto é MONOssódico né?!
Resposta
Exercício Resolvido #10
Unicamp – Química Geral e Inorgânica. Prof. Nelson. P3 – 2015.1. Questão 03. Modificada.
O gás cianogênio é composto de 46,2% de C e 53,8% de N em massa. A 25°C e 751 torr, 1,05 g deste gás tóxico ocupa 500 mL. Considerando que o gás tenha comportamento ideal, defina a fórmula molecular desse gás.
Dados:
R = 0,082 L.atm/mol.K
1 torr = 0,0013 atm
g/mol
g/mol
Lei dos gases ideais:
Passo 1
A questão envolve essa parte de gases ideais que talvez você ainda não tenha estudado.
Mas vamos no passo-a-passo que vai dar tudo certo!
Para transformar a composição percentual em fórmula molecular, começamos “fingindo” que temos uma amostra de 100 g do gás. Neste caso, teremos 46,2 g de C e 53,8 g de N.
Com essas massas e as massas molares do C e do N, vamos calcular o número de mols de C e N na fórmula mínima.
Então a proporção molar entre C e N no gás cianogênio é de 1:1. E a fórmula mínima será dada por: .
Mas a fórmula molecular pode ser: , , ...
Para transformar a fórmula mínima em fórmula molecular, precisamos conhecer a massa molar do composto.
Passo 2
Pra isso, vamos utilizar a lei dos gases ideais, que nos diz o volume () ocupado por determinado número de mols () de um gás, dada determinada condição de temperatura () e pressão ():
Onde é a constante dos gases ideais.
Pelo enunciado temos que:
Observe que o “definiu” quais unidades a gente precisou usar pra .
Calculando então:
O enunciado nos diz, ainda, que a amostra é de g do gás.
Podemos então calcular a massa molar do gás por:
Passo 3
Para a determinação da fórmula molecular, dividimos a massa molar pela massa molar da fórmula mínima, obtendo:
Como precisamos de um valor inteiro, utilizamos a aproximação .
Portanto, a fórmula molecular será a fórmula mínima com os índices multiplicados pelo fator 2:
Resposta