29 – Pesquisadores que trabalham com polímeros, frequentemente registram os seus dados em unidades estranhas. Por exemplo, na determinação de massas molares de polímeros por osmometria, as pressões osmóticas são frequentemente registradas em gramas por centímetro quadrado (g cm-2), e as concentrações, em gramas por centímetro cúbico (g cm-3)

A) Com essas unidades, quais seriam as unidades de R na eq. de van’t Hoff?

B) Os dados da tabela a seguir, da pressão osmótica do polissobuteno em clorobenzeno, a 25°C, em função da concentração. A partir desses dados, determine a massa molar do polissobuteno fazendo o gráfico de П/c contra c.

C) Solventes teta são solventes para os quais o segundo coeficiente osmótico é zero; para solventes ‘ruins’, o gráfico é linear, e para ‘bons’ solventes é não linear. A partir do gráfico que foi feito, como você classificaria o clorobenzeno como solvente para o polissobuteno? Discuta o resultado em termos da estrutura molecular do polímero e do solvente.

D) Determine o segundo e o terceiro coeficientes osmóticos do virial fazendo o ajuste dos dados à equação da pressão osmótica na forma do virial.

Vamos agora atribuir as unidades para as constantes R e g:

Em unidades de joule, kelvin e mol, a constante dos gases ideais possui um valor de:

Vamos relembrar que a unidade de joule, J, é expressa em termos das unidades do SI como

Assim,

A constante da aceleração da gravidade possui um valor de:

Assim,

Convertendo para grama e centímetro:

B)

Com os dados fornecidos no enunciado, para baixas concentrações, até 0,033 g cm-3, plota-se o seguinte gráfico de П/c versus c:

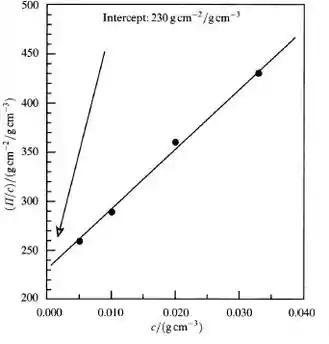
Pela equação de van’t Hoff, o coeficiente linear da reta da pressão osmótica dividida pela concentração, П/c, contra a concentração, c, que é exatamente o intercepto da reta, é dado por:

Assim, isolando M

Pelo gráfico

Assim,

Para sabermos se o clorobenzeno é um bom solvente ou não para o polissobuteno, vamos determinar o gráfico de П/c versus c em altas concentrações, pegando os dados da tabela fornecida, e se o gráfico tiver um comportamento não linear, o clorobenzeno será um bom solvente para o polissobuteno.

Com os dados em completo, plota-se o seguinte gráfico:

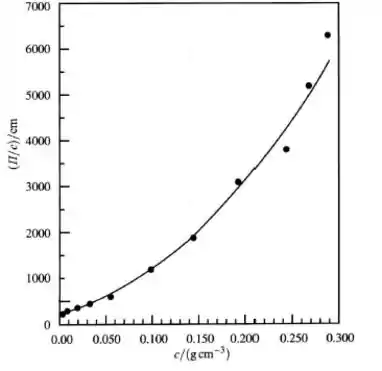
Pode-se ver que o comportamento da curva segue um padrão não linear, assim o clorobenzeno é um bom solvente.

Como achamos anteriormente, o clorobenzeno é um bom solvente para o polissobuteno, isso pode ser explicado pelas suas estruturas moleculares.

O clorobenzeno, possui uma característica de não polaridade em sua molécula, ou seja, é uma molécula apolar devido a presença do anel aromático. O polissobuteno também é uma molécula apolar, por possuir em sua molécula canônica, isto é, o monômetro, constituída por uma cadeia de hidrocarbonetos.

Com isso, devido a essa similaridade de natureza apolar em suas moléculas, o clorobenzeno acaba tendo uma grande interação intermolecular com o polissobuteno e sendo assim servindo bem como um solvente para o polissobuteno.

D)

A equação da pressão osmótica na forma do virial é:

Podemos rearranjar a expressão acima e coloca-la na forma de uma equação da reta, para que depois consigamos fazer um ajuste a uma reta e determinarmos o segundo e o terceiro coeficientes do virial (B’ e C’, respectivamente). Rearranjando,

Dividindo por c:

Assim, o segundo coeficiente do virial, B’, será o coeficiente linear da eq. da reta acima, e o terceiro coeficiente do virial, C’, será o coeficiente angular da reta.

Para você obter a estes coeficientes, você pode fazer uma regressão linear para o gráfico dado pela seguinte relação:

Obtém-se a seguinte equação da reta, obtida pelo ajuste dos dados a uma reta:

Assim,