Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 2.Problemas Numéricos - Ex. 1

Uma amostra consistindo em 1 mol de um gás perfeito monoatômico, com Cvm=3R/2, efetua o ciclo da figura. (a) calcule as temperaturas 1, 2 e 3. (b) Calcule q ,   w ,   ∆ U   e   ∆ H para cada etapa do ciclo e para todo o ciclo. Se a resposta numérica não for possível de ser obtida a partir da informação fornecida, escreva +, -, 0, ou ?, conforme o apropriado.

Passo 1

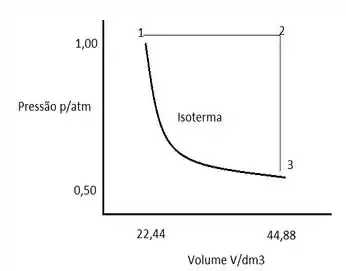
Esse gráfico assusta, mas calma que nós vamos desmembrar ele!

Logo de início a questão nos pede para calcular as temperaturas de 1,2 e 3. Para isso, nós usamos a fórmula:

T = p V n R

Aqui olhamos a tabela e pegamos o volume para 1, 2 e 3, sendo respectivamente: 22,4; 44,88 e 44,8. Também pegamos na tabela os valores de p sendo eles: 1;1 e 0,5. A variável n será de 1 mol para todos e o valor R já temos tabelado (0,0821 d m 3   a t m   m o l - 1 K - 1 ).

Agora jogamos os dados na fórmula:

T 1 = 1 a t m × 22,4   d m 3 1   m o l   ×   0,0821   d m 3   a t m   m o l - 1 K - 1 = 273   K

T 2 = 1 a t m × 44,8   d m 3 1   m o l   ×   0,0821   d m 3   a t m   m o l - 1 K - 1 = 546   K

T 3 = 0,5 a t m × 44,8   d m 3 1   m o l   ×   0,0821   d m 3   a t m   m o l - 1 K - 1 = 273   K

Passo 2

Agora vamos calcular q ,   w ,   ∆ U   e   ∆ H para e t a p a   1 → 2  

Para calcular o trabalho faremos:

w = - n R ∆ T

Todos esses dados nós já possuímos então basta aplicar:

w = - ( 1 m o l ) ( 8,3114   J K - 1 m o l - 1 ) ( 546 - 273 ) K

w = - 2,27   K J

Para variação de energia interna, a questão também já nos forneceu todas as informações:

∆ U = n C v m ∆ T

∆ U = 1   m o l 3 / 2 ( 8,3114   J K - 1 m o l - 1 ) ( 273 K )

∆ U = 3,4   K J

O calor será dado por:

q = ∆ U - w

q = 3,4   K J - ( - 2,27   K J )

q = 5,67   K J

A variação de entalpia será igual ao calor portanto:

∆ H = q = 5,67   K J

Passo 3

Agora vamos calcular q ,   w ,   ∆ U   e   ∆ H para e t a p a   2 → 3  

Como estamos tratando aqui de uma reação com volume constante não ocorre trabalho, portanto:

w = 0

O calor e a variação de energia interna serão iguais e dados por:

q = ∆ U = n C v m ∆ T

q = ∆ U = 1   m o l 3 / 2 ( 8,3114   J K - 1 m o l - 1 ) ( - 273 K )

q = ∆ U = - 3,4   K J

A variação de entalpia será:

∆ H = ∆ U + n R ∆ T

∆ H = - 3,4   K J + ( 1   m o l ) ( 8,3114   J K - 1 m o l - 1 ) ( - 273   K )

∆ H = - 5,67   K J

Passo 4

Agora vamos calcular q ,   w ,   ∆ U   e   ∆ H para e t a p a   3 → 1  

Aqui estamos em um processo isotérmico, então temos que ∆ U   e   ∆ H são zero.

O calor despendido será o inverso do trabalho sendo dado por:

w = - q = - n R T l n l n   V 1 V 3  

w = - q = ( - 1 ) ( 8,3114   J K - 1 m o l - 1 ) ( 273   K ) l n ( 22,4 44,8 d m 3 )

w = - q = 1,57   K J

Passo 5

Agora vamos calcular q ,   w ,   ∆ U   e   ∆ H para o ciclo. Para saber isso basta somar os resultados obtidos para cada etapa chegaremos a:  

  w = - q = 0,70   K J ; ∆ U =   ∆ H = 0,70   K J  

Resposta

T 1 = 273   K = T 3

T 2 = 546 K

E t a p a   1 → 2  

w = - 2,27   K J ;   q = + 5,67   k j   ∆ U = + 3,4   K J ;   ∆ H = + 5,67   K J  

E t a p a   2 → 3  

w = 0 ;   q v = ∆ U = - 3,4   K J ;   ∆ H = - 5,67   K J  

E t a p a   3 → 1  

w = - q = + 1,57   K J ;   ∆ U = ∆ H = 0  

C i c l o

w = - q = 0,70   K J ; ∆ U =   ∆ H = 0,70   K J  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um certo líquido tem ∆ v a p H + = 32,0K Jm o l - 1 . Calcule q ,w , ∆ He∆ U , quando se vaporiza 0,70 mol do líquido a 260 K e 765 Torr.
3.6 (b) Um sistema constituído por 1,5 mol de C O 2 g , inicialmente a 15°C e 9 atm, é confinado num cilindro de seção reta uniforme de 100,0 cm^2, provido de um pistão móvel. O gás se expande adiabat
3.4 (b) Uma amostra de 2,00 mol de um gás perfeito diatômico, a 250 K, é comprimida reversível e adiabaticamente até sua temperatura chegar a 300 K. Dado que C V , m = 27,5JK - 1 g - 1 , calcule q ,w
3.6 (a) Um sistema constituído por 2,0 mol de C O 2 g , inicialmente a 25°C e 10 atm, é confinado num cilindro de seção reta uniforme de 10,0 cm^2, provido de um pistão móvel. O gás se expande adiabat
3.4 (a) Uma amostra de 3,00 mol de um gás perfeito diatômico, a 200 K, é comprimida reversível e adiabaticamente até sua temperatura chegar a 250 K. Dado que C V , m = 27,5JK - 1 g - 1 , calcule q ,w