Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 2.1 - Ex. 105
(a)Mostre que as energias de rede são inversamente proporcionais à distância entre os íons em MX (M = metal alcalino, X = íons halogeneto), lançando em gráfico as energias de rede de KF, KCl e KI contra as distâncias internucleares, dM-X . As energias de rede de KF, KCl e KI são 826,717 e 645 kJ.mol-1, respectivamente. Use os raios iônicos encontrados no Apêndice 2D para calcular dM-X. Será que a correlação é boa? Você deve usar um programa gerador de gráficos padrão para construir o gráfico. Ele gera uma equação para a reta e calcula um coeficiente de correlação. (b) Estime a a energia de rede do KBr a partir de seu gráfico. (c) Encontre um valor experimental para a energia de rede do KBr na literatura e compare esse valor com o calculado em (b). Eles concordam?
Passo 1
Nossa, esse enunciado é bem grande e confuso. Vamos então distrinchá-lo para entender melhor. Temos que provar que as energias de rede são inversamente proporcionais á distância entre os íons em MX. Como vamos fazer isso? Através de um gráfico.
Então, primeiro passo é fazer um gráfico para coletar as duas informações que serão plotadas no gráfico.
Para testarmos se a correlação do gráfico é boa, temos que checar a informação do R2. Que deve ser o mais próximo de 1 possível.
Depois disso, vamos testar a qualidade do gráfico com outro halogênio, o Br. Primeiro a partir do gráfico, depois comparando com a literatura.
Passo 2
Vamos começar construindo uma tabela. Com os dados da questão e os valores do Apêndice 2D.
Agora, com auxílio do Excel, vamos montar este gráfico.
Passo 3
Com a ajuda do Excel montamos o seguinte gráfico:
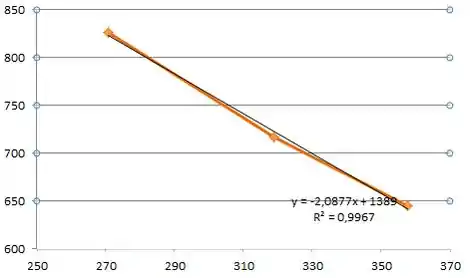
Temos como resultado, a equação da reta:
Y= -2,0877 X + 1389
R2 = 0,9967
Como R2 é aproximadamente 1, podemos considerar que a correlação é boa.
Passo 4
Agora, vamos estimar a energia de rede de KBr pelo gráfico encontrado. Temos, portanto, a equação da reta. Y= -2,0877 X + 1389
Olhando no Apêndice 2D, temos a distância 334 pm.
Queremos a energia de rede, logo, eixo Y. Portanto,
Y= -2,0877. 334 +1389
Y= 691,7082 kJ/mol
Passo 5
Agora, buscamos o valor da energia de rede na literatura, temos que a energia de rede do KBr é 689 kJ/mol. Este valor é muito próximo do achado pelo nosso método gráfico, ou seja, eles coincidem.
Resposta
(a) Y= -2,0877 X + 1389
R2 = 0,9967
(b) Y= 691,7082 kJ/mol
(c) Coincidem.