Nesta tarefa, precisamos calcular E° para a reação dada. Então, precisamos escrever uma notação e uma equação da célula. Por fim, precisamos calcular o pI da célula.

1. Podemos calcular E° da célula usando uma equação de Nernst:

onde E é o potencial da célula, E° é o potencial padrão da célula, n é o número de elétrons transferidos, [produtos] são concentrações de produtos elevados a uma potência de seus coeficientes estequiométricos, e [reagentes] são concentrações de reagentes elevadas a uma potência de seus coeficientes estequiométricos.

Como podemos ver pela reação, é reduzido a Pb sólido. Reescreva a reação de redução e encontre seu potencial padrão de redução no Apêndice 5:

Como podemos ver, E° é -0.126 V e o número de elétrons transferidos é 2.

Agora podemos inserir os dados da reação anterior na equação de Nernst:

Como as concentrações de sólidos e líquidos puros são constantes, não precisamos incluir o Pb sólido no termo do logaritmo:

Observe que precisamos calcular a concentração de . Para isso, podemos usar a constante do produto de solubilidade de para expressar a concentração de . A constante pode ser encontrada no Apêndice 3.

Lembre-se de que a constante do produto de solubilidade é uma constante de equilíbrio para uma espécie sólida dissolvida em uma solução aquosa. É igual ao produto da concentração de íons elevada pela potência de seus coeficientes estequiométricos. A equação geral para calculá-lo é:

onde A é o cátion da espécie, a é o coeficiente estequiométrico do cátion, B é o ânion da espécie e b é o coeficiente estequiométrico do ânion.

Passo 2

Agora podemos escrever a constante do produto de solubilidade de usando a equação geral

Divida a equação com então você obtém termo sozinho:



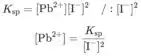
Observe que temos na equação de Nernst, então precisamos reverter a concentração de :





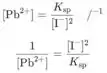
Observando o Apêndice 3, a constante do produto de solubilidade de é então a concentração inversa de é:

Agora podemos inserir a concentração calculada na equação de Nernst e calcular o potencial da célula:



2. Nesta tarefa, precisamos descrever uma célula usando uma notação se a célula consiste em um eletrodo de calomelano saturado e um eletrodo indicador de chumbo.

A notação geral de uma célula para análise potenciométrica é:

Para nossa tarefa, eletrodo de referência é um eletrodo de calomelano padrão (ECP), a solução de analito consiste em e solução saturada de , e eletrodo indicador é o eletrodo condutor.

Agora podemos escrever uma notação para a tarefa b):

3. Nesta tarefa, precisamos escrever uma equação que defina o potencial da notação da tarefa b). Para fazer isso, podemos usar a equação 21-1 que leva em consideração o potencial de dois eletrodos na célula:

A Equação 21-1 para nossa tarefa é:

Primeiro, podemos calcular o potencial de célula. A equação de Nernst para isso é:



Lembre-se que as concentrações de sólidos e líquidos puros são constantes, então não precisamos incluir [] na equação de Nernst. Além disso, calculamos na tarefa a).

Passo 3

Potencial do indicador eletrodo é:



Lembre-se que pI pode ser calculado a partir de [] desta forma:

Se substituirmos o termo do logaritmo por , a equação para calcular o potencial de

é:



O potencial do ECP pode ser encontrado no Apêndice 5 em mercúrio em KCl saturado:

Agora podemos inserir o potencial de dois eletrodos na equação 21-1:

Se subtrairmos dois valores potenciais, obtemos:

Para obter uma equação para pI, inverta os lados esquerdo e direito da etapa anterior:

Coloque 0,110 no lado direito:

Coloque 0,110 no lado direito:

4. Por fim, precisamos calcular o pI da célula se o potencial for -0,348 V. Basta inserir o valor do potencial na equação da tarefa c):