Enunciado
Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 6.Problemas Numéricos - Ex. 10
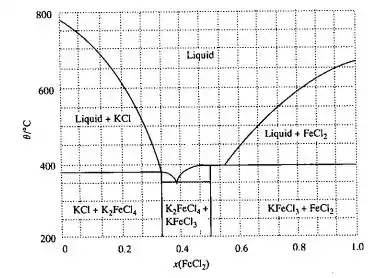
O cloreto de ferro (II) (PF de 677°C) e o cloreto de potássio (PF 776°C) formam os componentes KFeCl3 e K2FeCl4, a temperaturas elevadas. O KFeCl3 se funde congruentemente a 380°C e o K2FeCl4 incongruentemente a 399°C. Formam-se eutéticos com as seguintes composições (com x sendo a fração molar do FeCl2 e com a temperatura eutética sendo dada entre parênteses): a x =0,38 (fundindo-se a 351°C) e a x = 0,54 (fundindo-se a 393°C). A curva de solubilidade KCl encontra a curva do K2FeCl4 em x = 0,34. Esboce o diagrama de fases. Dê as fases em equilíbrio quando se resfria uma mistura a composição x = 0,36 de 400°C até 300°C.
Passo 1
E aí galerinha, tudo bem? Vamos para mais um desafio da físico-química juntos? Então, primeiramente vamos plotar os dados que nos foram cedidos no enunciado. Em 360°C, K2FeCl4(s) aparece. A solução começa a ficar cada vez mais rica em FeCl2 até que a gente consiga atingir uma temperatura de 351°C, nesse ponto temos agora que também o nosso amiguinho KFeCl3(s) começa a aparecer também. Por sua vez, abaixo de 351°C o sistema é uma mistura desses dois componentes que a gente viu, que seria uma mistura de K2FeCl4(s) e KFeCl3(s). E aí assim nosso diagrama fica da seguinte forma:
Resposta
Ei, a resposta está no passo a passo :)