Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 13.Problemas Numéricos - Ex. 5

A constante de rotação do CO é 1,9314   c m - 1 no estado fundamental e 1,6116   c m - 1 no primeiro estado excitado de vibração. De quanto se altera a distância entre os núcleos em consequência dessa transição?

Passo 1

Falaaaaaaaaaaaaaaaa Tribuxo?

Bora resolver mais uma questão!?

Vamos começar entendendo o que o exercício quer, ele quer saber de quanto se altera a distância entre os núcleos, para isso primeiro precisamos saber a fórmula da distância do núcleo:

I = m e f f R 2

Mas quem é I , podemos achá-lo por:

B = ℏ 4 π c I

Isolando I :

I = ℏ 4 π c B

Agora só precisamos substituir na primeira fórmula:

R 2 = ℏ 4 π c m e f f B

Onde h constante de Planck, c velocidade da luz, B constante rotacional, e:

m e f f = m C m O m C + m O   .   1,66054 × 10 - 27

Como estamos com um estado fundamental e outro excitado acharemos R 0 2 para o fundamental e R 1 2 para o excitado.

Passo 2

Vamos começar achando m e f f :

m e f f = m C m O m C + m O .   1,66054 × 10 - 27

m e f f = 12   .   16 12 + 16 .   1,66054 × 10 - 27

m e f f = 1,139 × 10 - 26   k g

Passo 3

Agora para encontrar os R 0 2 e R 1 2 :

R 2 = ℏ 4 π c m e f f B

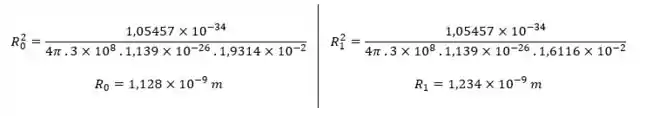
A gente pode fazer uma comparação em porcentagem:

1,234 × 10 - 9 - 1,128 × 10 - 9 1,128 × 10 - 9   .   100 = 9 , 397 %

Bora matar mais uma!

Resposta

R 0 = 1,128 × 10 - 9   m

R 1 = 1,234 × 10 - 9   m

Variou 9,397 % .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na constelação de Ofiúco (Serpentário) há uma nuvem de gás interestelar iluminada pela estrela τ -Ofiuci. A análise das linhas de absorção de Fraunhofer, no espectro de rotação, vibração e eletrônico
A proteína hemoritrina é responsável pela ligação e transporte de O, em alguns invertebrados. Cada molécula de proteína tem dois íons Fe2+ muito próximos e que atuam conjuntamente para ligar uma moléc
Uma mistura de dióxido de carbono (2,1%) e hélio, a 1,00 bar e 258K e numa célula de gás de 10 cm de comprimento, tem uma banda de absorção no infravermelho centrada em 2349 cm-1, com absorvâncias, A(
Calcule a separação, em frequência, dos níveis de energia dos estados do spin nuclear do núcleo de 13C num campo magnético de 14,4 T, sabendo razão giromagnética é de 6,73 × 10 7T - 1 s - 1 .
Calcule a separação, em frequência, entre os níveis de energia dos estados do spin nuclear do núcleo de 14N num campo magnético de 15,4 T, sabendo razão giromagnética é de 1 , 9 3 × 10 7T - 1 s - 1 .