Uma mistura de dióxido de carbono (2,1%) e hélio, a 1,00 bar e 258K e numa célula de gás de 10 cm de comprimento, tem uma banda de absorção no infravermelho centrada em 2349 cm-1, com absorvâncias, A(), dadas por
onde os coeficientes são a1= 0,932, a2= 0,005050 cm², a3= 2333 cm-1, a4= 1,504, a5= 0,01521 cm², e a6 = 2362 cm-1.
(a) Faça gráficos de A, e de ɛ Qual é a origem da banda e da largura da banda? Quais são as transições permitidas e proibidas dessa banda?
(b) Calcule os números de onda das transições e as absorvâncias da banda usando o modelo simples do oscilador harmônico e do rotor rígido e compare os resultados com os espectros experimentais. O comprimento da ligação do CO é de 116,2 pm.
(c) Em que altura, h, a radiação emitida da superfície da terra nessa banda é quase que totalmente absorvida pelo dióxido de carbono atmosférico? A fração molar do CO2, na atmosfera é 3,3x 10-4 e T/K = 288 – 0,0065(h/m) abaixo de 10 km. Represente graficamente uma superfície da transmitância atmosférica da banda em função da altura e do número de onda.
Passo 1
E aii, pessoal!! Essa questão traz uma concretização de entendimento sobre muito do que está presente na seção 13. Então, vamos revisar e entender melhor.
Começando pela letra a, como sabemos, a absorção molar do coeficiente ɛ é dada pela seguinte equação, que pode ser encontrada na seção 13.4, 1.8 e 1.15.
em que T=298K, l=10cm, p= 1 bar e xCO2=0.021.
A banda de absorção se origina com a transição de 001 ← 000 do modo vibratório de estiramento antissimétrico em 2349 cm-1 (Figura 13.40). A banda é muito ampla por causa das transições rotacionais e do alargamento da vida útil de cada absorção individual (também chamado de alargamento de pressão, presenta na seção 13.3).
O espectro revela que o ramo Q está faltando, então concluímos que a transição ∆J = 0 é proibida (Seção 13.12) para o grupo de pontos D∞ de CO2. O ramo P (∆J = -1) é evidente em energias mais baixas e o ramo R (∆J = 1) é evidente em energias mais altas. Agora, vamos revisar as figuras 13.6 a e b, presentes na seção do livro, para demonstrarmos os gráficos:
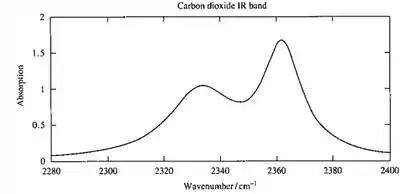
Figura 13.6 (a).
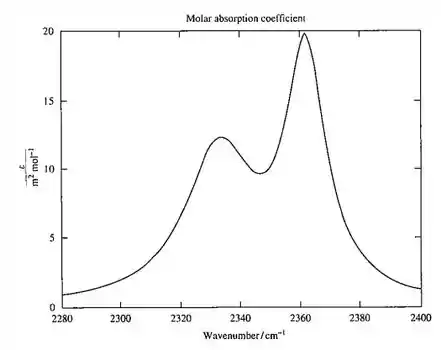
Figura 13.6 (b)
Passo 2
Na letra b, a molécula 160-12C-160 tem dois núcleos idênticos de spin zero, de modo que a função de onda do CO2 deve ser um intercâmbio nuclear w/r/t e deve obedecer às estatísticas nucleares de Bose-Einstein (da seção 13.8). Consequentemente, J assume valores pares apenas para o estado vibracional v = 0 e valores ímpares apenas para o estado v = 1. Os estados (v, J) para esta banda de absorção são (1, J + I) ← (0, J) para J = 0,2,4,...
De acordo com a eq. 13,61, a energia do estado simétrico (0, J) é:
Em que
Além disso,
Assim, encontramos B:
As transições dos ramos P e R ocorrem em
.
A maior transição de energia do ramo P está em ; a transição de energia mais baixa do ramo R está em + 2B. As transições são separadas por 4B (1,5608 cm-1) dentro de cada ramificação. A probabilidade de cada transição é proporcional à população do estado inferior, que presumimos ser dada pela distribuição de Boltzman com uma degenerescência de 2J +1. A probabilidade de transição também é proporcional a um fator de degenerescência nuclear (eq. 13,43) e a um momento de dipolo de transição, que é aproximadamente independente de J. Os primeiros fatores são absorvidos pela constante de proporcionalidade:
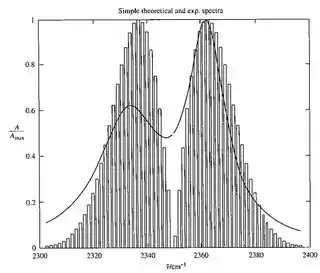
Um gráfico do lado direito desta equação contra J em 298 K indica uma probabilidade de transição máxima em Jmax =16. Nós "normalizamos" o máximo na estrutura prevista e eliminamos a probabilidade:
O gráfico, Figura 13.6 (c), da razão acima contra os números de onda previstos pode ser comparado à razão A ()/Amax onde Amax é o espectro máximo observado (1,677). Isso nos mostra um bom grau de concordância entre as formas de banda experimental e teórica simples.
Passo 3
Para a letra c, usando as equações da justificativa 13.1, podemos escrever a relação
A forte absorção da banda sugere que h não deve ter um comprimento muito grande e que [CO2] deve ser constante entre a superfície da Terra e h. Consequentemente, a integração dá
A lei de Dalton das pressões parciais p e T não devem mudar muito para valores modestos de h, então estimamos que p = 1 bar e T =288 K.
O gráfico da superfície de transmitância, Figura 13.6 (d), mostra claramente que antes que uma altura de cerca de 30m fosse alcançada, toda a radiação IV da Terra na faixa de 2320-2380 cm-1 foi absorvido pelo dióxido de carbono atmosférico.
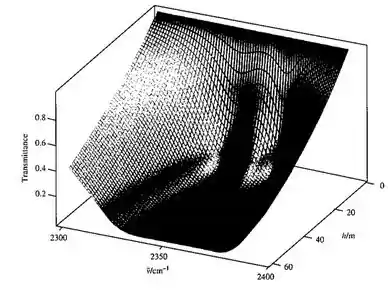
Figura 13.6(d).
Resposta
Ei, a resposta está no passo a passo :)