Desenhe um diagrama de níveis de energia de orbitais (como os das Figs. 16.27 e 16.29) mostrando a configuração dos elétrons d sobre o íon de metal nos seguintes complexos:
- ;
- ;
- ;
- ;
Preveja o número de elétrons não emparelhados para cada complexo.
Passo 1
Bora galera, começar mais uma!
Aqui nós temos seis ligantes monodentados, ou seja, o numero de coordenação do metal é seis.
Com isso podemos saber a estrutura formada, certo? Advinham qual?
Acertou quem disse octaédrica, ok?! Então já sabemos qual diagrama devemos usar, Fig 16.27.
Para completar precisamos saber dos elétrons de valência do cobalto, faremos isso do mesmo jeito que fizemos no exercício passado:
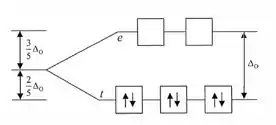
[Co3+] =[Ar] 3d6
Então temos seis elétrons na camada de valência.
Começamos a distribuí-los nos níveis menos energéticos:
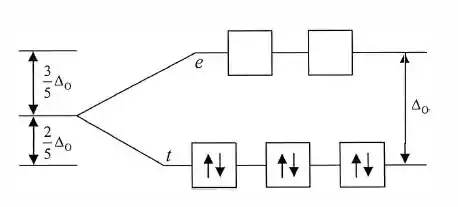
Nenhum elétron desemparelhado e, por isso, esta molécula é diamagnética.
Próximaa!
Passo 2
Já na letra b temos quatro ligantes monodentados, ou seja, o numero de coordenação do metal é quatro.
Ou seja, estrutura tetraédrica ! Então usaremos o diagrama da Fig 16.29.
Para completar precisamos saber dos elétrons de valência do níquel:
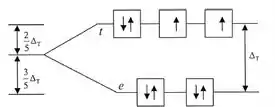
[Ni2+] =[Ar] 3d8
Então temos oito elétrons na camada de valência.
Começamos a distribuí-los nos níveis menos energéticos e vamos subindo, ok?
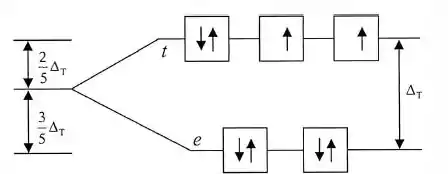
Temos dois elétrons desemparelhados, molécula paramagnética.
Passo 3
Na letra c faremos a mesma coisa. Com seis ligantes monodentados sua geometria será novamente octaédrica, Fig 16.27.
Para completar precisamos saber dos elétrons de valência do ferro:
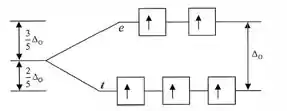
[Fe3+] = [Ar] 3d5
Então temos cinco elétrons na camada de valência. Como o ligante possui o campo fraco, os campos de energia estão mais próximos, logo devemos esperar que os elétrons ocupem todos os orbitais vazios, resultando em um número máximo de elétrons desemparelhados:
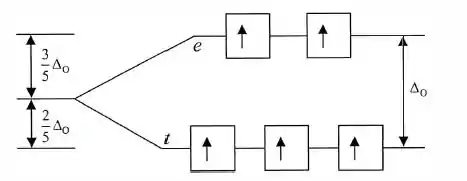
Sendo assim, temos 5 elétrons desemparelhados !
Passo 4
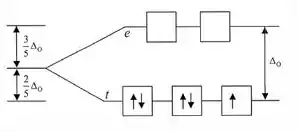
Na letra d temos a mesma configuração eletrônica da anterior, só que o ligante aqui é de campo forte.
Nestes casos, os níveis de energia estão muito separados e devemos esperar que os elétrons se emparelhem nos orbitais de energia mais baixa, resultando em menos elétrons desemparelhados:
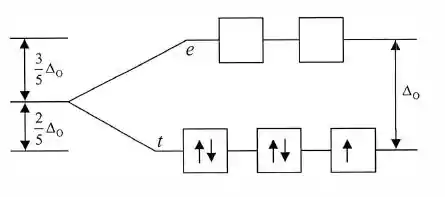
Por isso, um elétron desemparelhado.
Mais uma prontinha galeraaa!
Resposta
- Elétrons desemparelhados: 0
- Elétrons desemparelhados: 2
- Elétrons desemparelhados: 5
- Elétrons desemparelhados: 1