Enunciado
Física - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 15.Problemas Numéricos - Ex. 5
5 – Diversas versões da eq. de Karplus (eq. 15.27) foram usadas para correlacionar os dados das constantes de acoplamento de prótons vicinais em sistemas do tipo R1R2CHCHR3R4. A versão original é
Quando R3=R4=H, JHH=7,3 Hz. Quando R3=CH3 e R4=H, JHH=8,0 Hz. Quando R3=R4=CH3, JHH=11,2 Hz. Admita que apenas as conformações escalonadas sejam importantes e determine qual versão da equação de Karplus melhor se ajusta aos dados experimentais.
Passo 1
Como foi dito no enunciado, é razoável de se considerar que somente as conformações escalonadas são importantes. Estas conformações são mostradas no esboço abaixo.
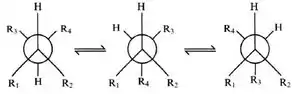
A ideia deste exercício então é calcular os valores das constantes de acoplamento, J, para cada tipo de conformação, a trans e cis, com base nos valores das constantes de acoplamento, JHH, obtidas experimentalmente, e a partir dos valores de J para conformação trans e cis, usar a equação original para verificar se é possível encontrar uma solução para as constantes A e B da equação que satisfaçam relação matemática com os dados experimentais.
Passo 2
Vamos precisar então determinar os valores para as constantes de acoplamento J das conformações trans e cis, onde vamos denominar o índice t para trans e c para cis
-Para quando R3=R4=H:
-Para quando R3=H e R4=CH3:
-Para quando R3=R4=CH3:
Precisamos achar os valores de Jt e Jc e temos três equações para isso, que são:
Já vemos pela Eq3 que Jt vale 11,2 e pegando as Eq’s 1 e 2 vamos ter que para Jc valores de 5,4 e 4,8, assim para Jc pegando um valor médio entre esses, vamos ter que:
Passo 3
Vamos agora determinar os valores das constantes A e B da equação original de Karplus, se for possível, usando os valores de Jt e JC encontrados
Para Jt:
O ângulo da conformação trans é
Assim,
Para Jc:
O ângulo da conformação cis é
Assim,
Para encontrarmos os valores de A e B vamos resolver o seguinte sistema linear, composto pelas eq’s 4 e 5:
Resolvendo este sistema encontramos que:
Você pode ver que conseguimos encontrar uma solução para as constantes A e B, dessa forma, como foi possível encontrar essa solução, pode-se dizer que essa versão original da eq. de Karplus se ajusta bem aos dados experimentais.
Passo 4
Vamos agora verificar a versão da eq. de Karplus dada pela Eq. 15.27
A forma da equação 15.27 da equação de Karplus é:
Onde, as constantes A, B e C são determinadas empiricamente e seus valores são:
Agora, para verificar se está equação se ajusta bem aos dados experimentais, você pode simplesmente substituir os valores das constantes na equação anterior e verificar para cada valor de J das conformações trans e cis.
Para Jt:
Com
Para JC:
Com
Você pode perceber que os valores se afastam um pouco, dos valores calculados com os dados experimentais, então a equação original acaba sendo mais ajustada aos dados.
Resposta
Equação original se ajusta melhor aos dados experimentais.