Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 7.Problemas Numéricos - Ex. 15

Embora o eletrodo de hidrogênio seja conceitualmente o eletrodo mais simples, e seja a base do estado de referência dos potenciais elétricos dos sistemas eletroquímicos, ele é um dispositivo incómodo e difícil de operar. Nessas circunstâncias, imaginaram-se vários eletrodos para substituí-lo. Um eletrodo que pode ser usado em seu lugar é o eletrodo de quinidrona. A quinidrona ( Q . Q H 2 ) é um complexo da quinona,   C 6 H 4 O 2   =   Q . e da hidroquinona, C 6 H 4 O 2 H 2   =   Q . A meia-reação do eletrodo é Q a q +   2   H + a q +   2   e - → Q H 2 ( a q ) , e o respectivo potencial-padrão E o =   + 0,6994   V . Se tivermos a pilha H g H g 2 C l 2 s H C l a q |   Q   .   Q H 2 |   A u , e o potencial medido for + 0,190   V , qual o p H da solução de H C l ? Admita a validade da lei limite de Debye-Hückel.

Passo 1

Falaaaaaaaaaaaaaaaa Tribuxo?

Bora resolver mais uma questão!?

Vamos começar escrevendo as semirreações:

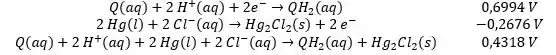
Escrevendo Q :

Q = a Q H 2 a Q a 2 H + a 2 C l -

Vamos ter:

m Q = m Q H 2

a Q H 2 ≈ a Q

Então:

Q = 1 a 2 H + a 2 C l -

Para achar o Q , vamos usar:

E = E o - 25,7 m V v ln ⁡ Q

0,190 = 0,4318 - 25,7 × 10 - 3 2 ln ⁡ Q

Q = 1,487 × 10 8

Teremos:

a 2 H + = γ + b + 2   ; a 2 C l - = γ - b - 2

b = b b o

Para o H C l , b + = b - = b ,assumindo a 2 H + = a 2 C l -

Q = 1 a 4 H +

Determinando α :

1,487 × 8 = 1 a 4 H +

α H + = 9,056 × 10 - 3

Agora para determinar o p H , temos:

p H = - log ⁡ a H +

p H = - log ⁡ 9,056 × 10 - 3

p H = 2,043

Foi divertido!!!!

Bora matar mais uma!

Resposta

p H = 2,043

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as pilhas que correspondem a cada uma das reações seguintes, e calcule a f e m em cada caso:a) Z n s + C u S O 4 a q → Z n S O 4 a q + C u s b) 2A g C l s + H 2 g → 2H C l a q + 2A g s c) 2H
A f e m da pilha A g A g I s A g I a q | A g é + 0,9509V , a 25°C. Calcule (a) o produto de solubilidade do A g I e (b) a sua solubilidade.
Uma pilha de combustível desenvolve um potencial elétrico a partir de uma reação química entre reagentes que são fornecidos por uma fonte externa. Qual é a f e m de uma pilha alimentada por (a) hidrog
Os elementos superpesados têm, nos dias de hoje, apreciável interesse, porque há indicios de estabilidade no elemento 114, obtido recentemente. Pouco antes de um rebate falso sobre a descoberta do pri
A fem da pilha P t | H 2 ( g , p º ) | H C l ( a q , b ) | H g 2 C l 2 , ( s ) | H g ( l ) º foi medida comgrande exatidão (G.J. Hills e D.J.G. Ives. J. Chem. Soc., 311 (1951)), com os seguintes resul