Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 29.Questões e Problemas - Ex. 10ab
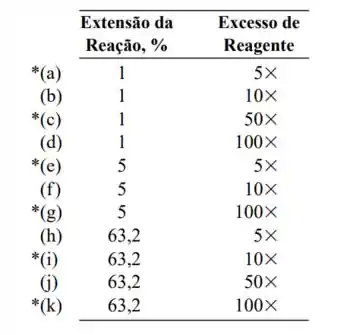
Encontre o erro relativo associado com a hipótese de que k’ não varia no decorrer de uma reação de pseudoprimeira ordem sob as seguintes condições.
Passo 1
Falaaaa moçadinha, show de bola?
Como diz o Homem de ferro “Eu tenho um plano. Ataque!”
Bora atacar esse problemaaaaaaa junto comigoo.
A nossa fórmula de erro relativo é expressa da seguinte maneira
Passo 2
- Extensão de reação
- Extensão de reação
Concentração de vezes mais do que
Considerando a seguinte reação
A concentração inicial do reagente é dada como
Com 1% de reação, 99% de A permanece
Desta maneira
A taxa de reação de 1% sob a condição de pseudo-condição de primeira ordem é dada como
é a taxa na reação de 1% e a taxa medida será:
Passo 3
Vamos substituir os valores na fórmula do erro relativo, portanto
Portanto, o erro relativo da reação dada é de
Passo 4
Concentração de vezes mais do que
Considerando a seguinte reação
A concentração inicial do reagente é dada como
Com 1% de reação, 99% de A permanece
Desta maneira
A taxa de reação de 1% sob a condição de pseudo-condição de primeira ordem é dada como
é a taxa na reação de 1% e a taxa medida será:
Passo 3
Vamos substituir os valores na fórmula do erro relativo, portanto
Portanto, o erro relativo da reação dada é de
“Às vezes é preciso aprender a correr antes de começar a andar”
Resposta
a) Portanto, o erro relativo da reação dada é de
b) Portanto, o erro relativo da reação dada é de