Enunciado
Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 12.Problemas Numéricos - Ex. 12
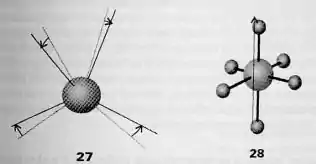
Um estudo computacional sobre os compostos AMX, em que A é um elemento do grupo 14 da tabela periódica e M um metal alcalino, mostra muitos desvios em relação às estruturas mais simétricas de cada fórmula. (a) Por exemplo, a maioria das estruturas AM4 não é tetraédrica, mas exibe dois valores diferentes dos ângulos MAM. Podem ser derivados do tetraedro regular pela distorção esquematizada na figura (27). Qual o grupo de simetria do tetraedro distorcido? (b) Qual é a espécie de simetria da deformação admitindo-se seja uma vibração num novo grupo menos simétrico? Algumas estruturas AM6 não são octaédricas, mas podem ser derivadas de um octaedro regular pela translação de um eixo C-M-C, como na figura (28). (c) Qual o grupo de simetria desse octaedro distorcido? (d) Qual é a espécie de simetria da distorção considerada como uma vibração no novo grupo, menos simétrico?
Passo 1
(a) Opaaaaa, gente!!! Pega aí o livro e dê uma olhadinha no diagrama que é a figura 12.7. Você vai perceber que há 3 Cn com n > 2, mas temos de fato mesmo mesmo mesmo 2 C2 perpendiculares nos quais podemos chamar dos eixos principais. Não temos nenhum , mas temos 2. Portanto o grupo de ponta é D2d
Passo 2
(b) Com esse grupo definido, a distorção pertence ao grupo totalmente simétrico que é o A1, pois seu movimento é inalterado pela operação S4, de igual forma para as operações C2 ou
Passo 3
(c) A estrutura resultado é uma bipiramidal quadrada, mas com um ápice da pirâmide mais distante da base do que a outra. Trabalhando com o fluxograma do diagrama da figura 12.7 do livro, nós notamos que há apenas 1 Cn, com n > 2, chamado de eixo C4, não há C2 perpendiculares ao C4, não temos , mas temos 4. Portanto, o grupo de ponta é o C4V.
Passo 4
(d) Com esse grupo, podemos definir também que a distorção pertence ao grupo de simetria totalmente simétrico que é o A1. A translação dos átomos ao longo do eixo é inalterado por qualquer operação de simetria pois o movimento é contido com cada elemento do grupo de simetria.
Resposta
Ei, a resposta está no passo a passo :)