Enunciado

Física - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 9.Problemas Teóricos - Ex. 22

22 – Use um software matemático para construir um pacote de ondas da forma

Com coeficientes c de sua escolha (por exemplo, todos iguais). Explore como o pacote de ondas migra sobre o anel, mas se espalha com o tempo.

Passo 1

Um software matemático que você pode usar para resolver este problema, é o Mathcad, assim também como o Matlab.

Usando estes softwares, pode-se construir o conjunto de ondas animando a parte real ou a parte imaginaria da função Ψ(φ, t). Os coeficientes c, para este problema serão adotados como sendo c = 1.

Passo 2

O gráfico obtido usando o Mathcad através da função de onda dada no enunciado, que representa o pacote de ondas, é:

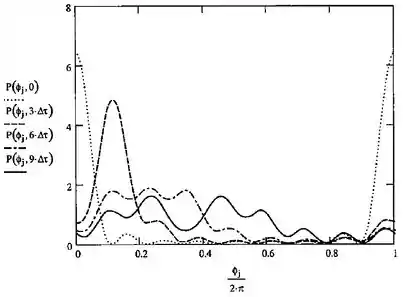
Passo 3

Vamos agora analisar o comportamento das ondas em relação ao tempo.

O gráfico anterior mostra que inicialmente as ondas se propagam ao redor do anel que se espalham com o tempo e a incerteza de se saber a posição da partícula aumenta. O efeito do aumento ou decréscimo da energia acessível para a partícula pode ser explorado pelo aumento ou redução do valor de mmáx.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se os orbitais px e py, são autofunções de Iz. Se não forem, haverá combinação linear que seja autofunção de Iz?

Tome como função de onda hipotética do estado fundamental do átomo de hidrogênio (a) e k r e (b) e - k r 3 , com o princípio variacional, estime o valor ótimo de k em cada caso. Identifique a melhor f

Calcule a correção de segunda ordem para a energia do sistema descrito no Problema 9.6 e calcule a função de onda do estado fundamental. Explique a forma da distorção causada pela perturbação. Sugestã

A função de onda no interior de uma barreira espessa, de altura V, é ψ = N e - k x . Calcule (a) a probabilidade de a partícula estar no interior da barreira e (b) a distância média de penetração da p

Veremos no Cap. 13 que as intensidades das transições espectroscópicas entre os estados de vibração de uma molécula são proporcionais ao quadrado da integral ∫ ψ v x ψ v d x sobre todo o espaço. Com a