- Desenhe os orbitais ligantes e antiligantes que correspondem à ligação em .
- Repita o procedimento para HF.
- Em que esses orbitais se diferem?
Passo 1
Boa galera, quando ocorre uma ligação entre duas moléculas há a formação de dois orbitais, que são chamados de ligantes e antiligantes.
Nos orbitais ligantes a densidade eletrônica, ou seja, os elétrons, estarão presentes entre os núcleos destas moléculas. Enquanto nos antiligantes isso não ocorre, e por isso é observado um “espaço” entre os átomos.
Tranquilo até aqui?
No caso do nós teremos dois orbitais 1s ligando entre si.
Quando estamos falando do orbital ligante, a densidade eletrônica irá preencher toda a extensão da molécula formada. Como assim?
Vamos desenhar:

Ao mesmo tempo em que este orbital é gerado, ocorre a formação do orbital antiligante. E neste caso não há densidade eletrônica entre os átomos:
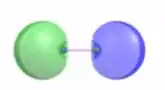
Como os átomos são iguais, os orbitais são simétricos. Mas isso não é o que acontece com o HF, porque teremos dois átomos diferentes.
Neste caso, o orbital p do flúor vai interagir com o orbital s do hidrogênio. Como o flúor é mais eletronegativo, a densidade eletrônica estará mais próxima a ele.
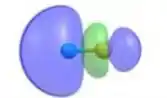
No caso dos orbitais ligantes :
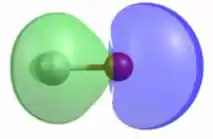
O elemento menos eletronegativo contribui mais fortemente para o orbital antiligante, então neste caso não vemos a ausência de densidade eletrônica entre os núcleos.
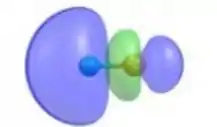
Passo 2
Na letra c nós queremos saber o motivo de serem tão diferentes.
Simples , não?
No caso do temos somente orbitais s interagindo, já no HF a ligação ocorre entre um orbital p e um s.
Então, a maior diferença entre eles se deve ao orbital p.
Resposta
- Ligante:

- Ligante:
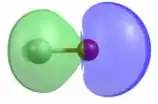
- Orbital p.
Antiligante: 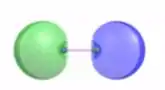
Antiligante: