Determine se a integral de f1 e f2 no exercício 12.15ª é nula sobre um intervalo simétrico em torno de no grupo C3V.
Passo 1
Bem, vamos fazer uma tabelinha aqui pro grupo C3V, beleza?
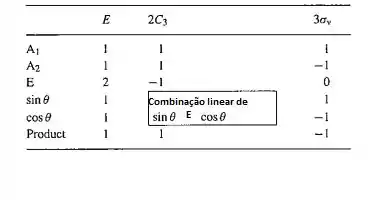
O produto não contem A1, portanto sim, a integral é nula!
Resposta
Ei, a resposta está no passo a passo :)