Enunciado
Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 12.Problemas Numéricos - Ex. 3
3 – O grupo D2h tem um eixo C2 perpendicular ao eixo principal e um plano de simetria especular horizontal. Mostre que o grupo tem, necessariamente, um centro de inversão.
Passo 1
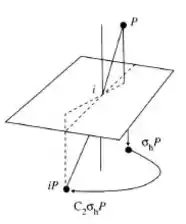
Para ficar mais claro a resolução deste problema, vamos analisar uma imagem tal como a imagem mostrada a seguir:
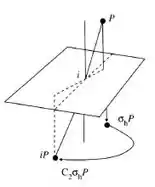
Passo 2
Pela imagem mostrada anteriormente, podemos fazer as seguintes análises e considerações acerca do centro de inversão.
O efeito de σh no ponto P acaba gerando o ponto composto por σhP, e o efeito de C2 em σhP é para gerar o ponto C2σhP.
O mesmo ponto é gerado do ponto P pela inversão i, então o ponto C2σhP = iP para todos os pontos P. Consequentemente, C2σh = i, e i deve ser um membro do grupo.
Com essa análise, pode-se dizer que existe um centro de inversão presente no grupo D2h.
Resposta
