Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 16.1 - Ex. 69

A melhor descrição dos orbitais t 2 g no [ C o ( O H 2 ) 6 ] 3 + (a) ligante (b) antiligante ou (c) não ligante? Explique como você chegou a essa conclusão.

Passo 1

Vamos começar mais umaa!

Antes de tudo desenhamos o nosso complexo:

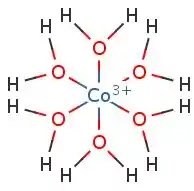
Reparem bem aqui! O complexo só possui ligações do tipo σ , não é?

Isso porque nosso ligante é a água, considerada como um ligante doador σ .

Nestes casos, o diagrama fica assim:

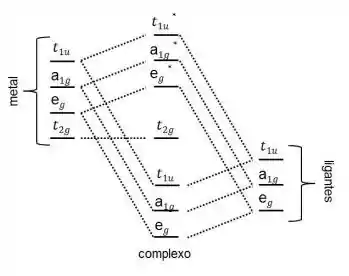
Por aqui já vemos que o orbital t 2 g é não ligante, já que não há orbital semelhante nos ligantes.

Portanto, os orbitais t 2 g são não ligantes ou ligeiramente antiligantes.

Por que ligeiramente antiligantes? Calma que eu explico!

Como a agua é uma base π fraca, como já vimos no exercício 67, o conjunto de orbitais t 2 g se torna ligeiramente antiligante devido a interação com os orbitais p completos dos ligantes.

Esta foi fácil, pronto pra outra?

Resposta

N ã o   l i g a n t e s   o u   l i g e i r a m e n t e   a n t i l i g a n t e s !

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a molécula H2O, que pertence ao grupo C2v. Tome como base os dois orbitais H1s e os quatros orbitais de valência do átomo de O e construa as matrizes 6 x 6 que representam o grupo nesta base
As clorofilas que participam da fotossíntese e os grupos heme dos citocromos são derivados do diânion porfirina (figura abaixo), que pertence ao grupo de simetria D4h. O estado eletrônico fundamental
As clorofilas que participam da fotossíntese e os grupos heme dos citocromos são derivados do diânion porfirina (figura abaixo), que pertence ao grupo de simetria D4h. O estado eletrônico fundamental
O íon molecular H3+ foi recentemente descoberto no meio interestrelar e também nas atmosferas de Júpiter, Saturno e Urano. Os análogos em H4 não foram ainda descobertos, e acredita-se que a estrutura
13 – Construa e resolva as equações seculares de Hückel para os elétrons π do NO3-. Expresse as energias em termos das integrais α0 e αN e da integral de ressonância β. Determine a energia de deslocal